推土机距离（Wasserstein distance）以及其他几种常用的分布差异度量方法（mark）

---

---

1. Wasserstein距离

1.1 方法简介
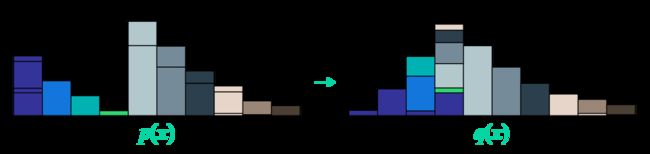
Wasserstein Distance也称为推土机距离（Earth Mover’s distance, EMD)，Wasserstein Distance的定义是评估由P分布转换成Q分布所需要的最小代价(移动的平均距离的最小值)→和挖东墙补西墙类似(把一个形状转换成另一个形状所需要做的最小工)，类似于把一块地方土挖出来，然后填平另一块地方，而W距离找的的是这一过程中挖每一方土最小需要消耗的能量，所以经常查到Wasserstein Distance称为推土机距离。

1.2 方法优势
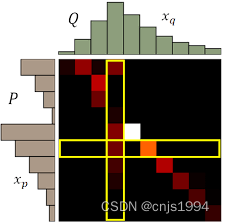
虽然KL散度和JS散度应用更为广泛，Wessertein距离相比KL散度和JS散度的优势在于：即使两个分布的支撑集没有重叠或者重叠非常少，仍然能反映两个分布的远近。而JS散度在此情况下是常量，KL散度可能无意义。
K-L 散度和 JS 散度取值是突变的，要么最大要么最小，Wasserstein 距离却是平滑的。如果我们要用梯度下降法优化参数，前两者根本提供不了梯度，Wasserstein 距离却可以。
1.3 应用：wikipedia[1]中给出的应用场景是The Wasserstein metric is a natural way to compare the probability distributions of two variables X and Y, where one variable is derived from the other by small, non-uniform perturbations (random or deterministic).翻译过来就是比较两个变量X和Y的概率分布的自然方法，其中一个变量是通过小的、非均匀的扰动（随机或确定性）从另一个变量推导出来的。由于其平滑性好，能够缓解梯度消失和模式崩溃问题。

想要更通俗易懂的解释可以看这个[2],

1.4 python实现
scipy库的实现,函数为 wasserstein_distance，输入参数包括：u_values, v_values以及u_weights, v_weights；weights如果不分配就是使用相同的权值；输出：就是得到的距离 。这个权值矩阵应该是相邻两个元素之间的“交通距离“啥的，[3]原话是：“# where distance between each pair of adjacent elements is 1”

from scipy.stats import wasserstein_distance
wd1 = wasserstein_distance([0, 1, 3], [5, 6, 8])
wd2 = wasserstein_distance([0, 1], [0, 1], [3, 1], [2, 2])
print(f"wasserstein_distance: {wd1}")

stackoverflow问答给的计算案例[3]

from scipy import stats

u = [0.5,0.2,0.3]
v = [0.5,0.3,0.2]

# create and array with cardinality 3 (your metric space is 3-dimensional and
# where distance between each pair of adjacent elements is 1
dists1 = [i for i in range(len(u))]
dists2 = [i for i in range(len(v))]

stats.wasserstein_distance(dists1, dists2, u, v)

结果打印出来：

dists1 = [i for i in range(len(u))]
print(f"dist1:{dists1}")

dists1=[0,1,2]

另一个比较通俗易懂的case，图文说明可以看这个博客[4]。移动的距离是只跨过的单位距离，比如0-3，就是距离3，移动的块是P-Q的变化过程 也就是1；第二个移动是P-Q移动两块，移动了3个距离，也就是3*2=6；第3次移动是移动1个块，也是移动了3个距离；总共移动了3+6+3=12；总共移动了4块；所以距离是4。

import scipy.stats
import numpy as np

P = np.array([1,2,1])
Q = np.array([1,2,1])
dists_P=[0,1,2]
dists_Q=[3,4,5]
D=scipy.stats.wasserstein_distance(dists_P, dists_Q, P, Q)
print(f"dist_P:{dists_P};dist_Q:{dists_Q};wasserstein_distance:{D}")

PS： 进阶内容可参考这个： https://pythonot.github.io/auto_examples/plot_gromov.html

2. KL散度

KL散度（Kullback-Leibler divergence，简称KLD）:

A. 在信息系统中称为相对熵（relative entropy）
B. 在连续时间序列中称为随机性（randomness）
C. 在统计模型推断中称为信息增益（information gain）。也称信息散度（information divergence）。

KL散度是用于衡量分布P相对于分布Q的差异性。典型情况下，P表示数据的真实分布，Q表示数据的理论分布、估计的模型分布、或P的近似分布

PS：这个指标不能用作距离衡量,因为其不具有对称性。
主要应用：
GAN网络：生成对抗网络（GAN）在图片上的应用往往执行的是类似基于黑白图片生成看起来尽量真实的彩色图片这样的任务。在这类似的应用中，输入往往是图像或像素。网络会学习这些像素之间的依赖关系（比如临近像素通常有相似的颜色），然后使用它来创建看起来尽量真实的图像。因此，生成器的目标就是最小化所学到的像素分布与真实图像像素分布之间的散度。简单来说，推土机距离寻找的是一个从一个分布变换到另一个分布的最小代价。

下面是python的一些代码、例子总结
首先，随机生成两个序列

# 随机生成两个离散型分布
x = [np.random.randint(1, 11) for i in range(10)]
print(x)
print(np.sum(x))
px = x / np.sum(x)
print(px)
y = [np.random.randint(1, 11) for i in range(10)]
print(y)
print(np.sum(y))
py = y / np.sum(y)
print(py)

计算kl散度的函数

def KL(px, py):
     kl_r = 0.0
     for i in range(10):
       kl_r += px[i] * np.log(px[i] / py[i])
     # print(str(px[i]) + ' ' + str(py[i]) + ' ' + str(px[i] * np.log(px[i] / py[i])))
     return kl_r 

测试结果

0.42884335724837774

2. 也可以使用scipy库函数

from scipy import *
def asymmetricKL(P,Q):
     return sum(P * log(P / Q)) #calculate the kl divergence between P and Q
def symmetricalKL(P,Q):
     return (asymmetricKL(P,Q)+asymmetricKL(Q,P))/2.00

测试结果

0.4288433572483777

另一个例子

import numpy as np
import scipy.stats

def KL_divergence(p,q):
    return scipy.stats.entropy(p, q, base=2)

p=[np.random.randint(1, 10) for i in range(10)]
q=[np.random.randint(1, 10) for i in range(10)]
print(KL_divergence(p, q)) # 0.22260851466766604
print(KL_divergence(q, p)) # 0.2668107727869456
print(KL_divergence(p, p)) # 0.0

3. JS散度

与KL类似，JS散度也是度量两个分布的相似性，越相似，JS散度越小。

1. JS散度的取值在0-1之间，完全相同为0
2. JS散度是对称的

import numpy as np
import scipy.stats
def JS_divergence(p,q):
    M=(p+q)/2
    return 0.5*scipy.stats.entropy(p,M,base=2)+0.5*scipy.stats.entropy(q, M,base=2)

p=np.asarray([np.random.randint(1, 10) for i in range(10)])
q=np.asarray([np.random.randint(1, 10) for i in range(10)])

print(JS_divergence(p, q))  # 0.07268409205373166
print(JS_divergence(q, p)) # 0.07268409205373166
print(JS_divergence(p, p)) # 0.0

参考资料

[1] wikipedia: https://en.wikipedia.org/wiki/Wasserstein_metric
[2] https://blog.csdn.net/qq_40394402/article/details/109565803
[3] https://stackoverflow.com/questions/60529232/reference-for-wasserstein-distance-function-in-python
[4] https://blog.csdn.net/weixin_44862361/article/details/125505769
[5]https://cloud.tencent.com/developer/article/1388597
[6] https://zhuanlan.zhihu.com/p/143105854/