数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}
题目出自阿里天池赛题链接:零基础入门数据挖掘 - 二手车交易价格预测-天池大赛-阿里云天池
相关文章:
特征工程详解及实战项目【参考】
数据挖掘---汽车车交易价格预测[一](测评指标;EDA)
数据挖掘机器学习---汽车交易价格预测详细版本[二]{EDA-数据探索性分析}
数据挖掘机器学习---汽车交易价格预测详细版本[三]{特征工程、交叉检验、绘制学习率曲线与验证曲线}
数据挖掘机器学习---汽车交易价格预测详细版本[四]{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}
数据挖掘机器学习---汽车交易价格预测详细版本[五]{模型融合(Stacking、Blending、Bagging和Boosting)}
数据挖掘机器学习[六]---项目实战金融风控之贷款违约预测
数据挖掘机器学习[七]---2021研究生数学建模B题空气质量预报二次建模求解过程
前言
因为文档是去年弄的,很多资料都有点找不到了,我尽可能写的详细。后面以2021年研究生数学建模B题为例【空气质量预报二次建模】再进行一个教学。
1 模型对比与性能评估
1.1 逻辑回归
相关文章:基于逻辑回归的分类预测,基于鸢尾花(iris)数据集分类、多分类实战
逻辑回归(Logistic regression,简称LR)虽然其中带有"回归"两个字,但逻辑回归其实是一个分类模型,并且广泛应用于各个领域之中。虽然现在深度学习相对于这些传统方法更为火热,但实则这些传统方法由于其独特的优势依然广泛应用于各个领域中。
而对于逻辑回归而且,最为突出的两点就是其模型简单和模型的可解释性强。
- 优点:实现简单,易于理解和实现;计算代价不高,速度很快,存储资源低;
- 缺点:容易欠拟合,分类精度可能不高
-
优点
- 训练速度较快,分类的时候,计算量仅仅只和特征的数目相关;
- 简单易理解,模型的可解释性非常好,从特征的权重可以看到不同的特征对最后结果的影响;
- 适合二分类问题,不需要缩放输入特征;
- 内存资源占用小,只需要存储各个维度的特征值;
-
缺点
-
逻辑回归需要预先处理缺失值和异常值;
-
不能用Logistic回归去解决非线性问题,因为Logistic的决策面是线性的;
-
对多重共线性数据较为敏感,且很难处理数据不平衡的问题;
-
准确率并不是很高,因为形式非常简单,很难去拟合数据的真实分布;
-
逻辑回归 原理简介:
Logistic回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别),所以利用了Logistic函数(或称为Sigmoid函数),函数形式为:
其对应的函数图像可以表示如下:
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-5,5,0.01)
y = 1/(1+np.exp(-x))
plt.plot(x,y)
plt.xlabel('z')
plt.ylabel('y')
plt.grid()
plt.show()逻辑回归的应用
逻辑回归模型广泛用于各个领域,包括机器学习,大多数医学领域和社会科学。例如,最初由Boyd 等人开发的创伤和损伤严重度评分(TRISS)被广泛用于预测受伤患者的死亡率,使用逻辑回归 基于观察到的患者特征(年龄,性别,体重指数,各种血液检查的结果等)分析预测发生特定疾病(例如糖尿病,冠心病)的风险。逻辑回归模型也用于预测在给定的过程中,系统或产品的故障的可能性。还用于市场营销应用程序,例如预测客户购买产品或中止订购的倾向等。在经济学中它可以用来预测一个人选择进入劳动力市场的可能性,而商业应用则可以用来预测房主拖欠抵押贷款的可能性。条件随机字段是逻辑回归到顺序数据的扩展,用于自然语言处理。
1.2. 决策树模型
- 优点
- 简单直观,生成的决策树可以可视化展示
- 数据不需要预处理,不需要归一化,不需要处理缺失数据
- 既可以处理离散值,也可以处理连续值
- 缺点
- 决策树算法非常容易过拟合,导致泛化能力不强(可进行适当的剪枝)
- 采用的是贪心算法,容易得到局部最优解
1.2.1 XGBoost
相关文章推荐:基于天气数据集的XGBoost分类实战
1.GBDT将目标函数泰勒展开到一阶,而xgboost将目标函数泰勒展开到了二阶。
2.xgboost加入了和叶子权重的L2正则化项,因而有利于模型获得更低的方差
3.xgboost增加了自动处理缺失值特征的策略。通过把带缺失值样本分别划分到左子树或者右子树,比较两种方案下目标函数的优劣,从而自动对有缺失值的样本进行划分,无需对缺失特征进行填充预处理。
XGBoost的主要优点:
- 简单易用。相对其他机器学习库,用户可以轻松使用XGBoost并获得相当不错的效果。
- 高效可扩展。在处理大规模数据集时速度快效果好,对内存等硬件资源要求不高。
- 鲁棒性强。相对于深度学习模型不需要精细调参便能取得接近的效果。
- XGBoost内部实现提升树模型,可以自动处理缺失值。
-
使用了许多策略去防止过拟合,如:正则化项
添加了对稀疏数据的处理
采用了交叉验证以及early stop,防止建树过深
XGBoost的主要缺点:
- 相对于深度学习模型无法对时空位置建模,不能很好地捕获图像、语音、文本等高维数据。
- xgBoosting采用预排序,在迭代之前,对结点的特征做预排序,遍历选择最优分割点,数据量大时,贪心法耗时,LightGBM方法采用histogram算法,占用的内存低,数据分割的复杂度更低;
XGBoost的重要参数
1.eta[默认0.3]
通过为每一颗树增加权重,提高模型的鲁棒性。
典型值为0.01-0.2。2.min_child_weight[默认1]
决定最小叶子节点样本权重和。
这个参数可以避免过拟合。当它的值较大时,可以避免模型学习到局部的特殊样本。
但是如果这个值过高,则会导致模型拟合不充分。3.max_depth[默认6]
这个值也是用来避免过拟合的。max_depth越大,模型会学到更具体更局部的样本。
典型值:3-104.max_leaf_nodes
树上最大的节点或叶子的数量。
可以替代max_depth的作用。
这个参数的定义会导致忽略max_depth参数。5.gamma[默认0]
在节点分裂时,只有分裂后损失函数的值下降了,才会分裂这个节点。Gamma指定了节点分裂所需的最小损失函数下降值。 这个参数的值越大,算法越保守。这个参数的值和损失函数息息相关。6.max_delta_step[默认0]
这参数限制每棵树权重改变的最大步长。如果这个参数的值为0,那就意味着没有约束。如果它被赋予了某个正值,那么它会让这个算法更加保守。
但是当各类别的样本十分不平衡时,它对分类问题是很有帮助的。7.subsample[默认1]
这个参数控制对于每棵树,随机采样的比例。
减小这个参数的值,算法会更加保守,避免过拟合。但是,如果这个值设置得过小,它可能会导致欠拟合。
典型值:0.5-18.colsample_bytree[默认1]
用来控制每棵随机采样的列数的占比(每一列是一个特征)。
典型值:0.5-19.colsample_bylevel[默认1]
用来控制树的每一级的每一次分裂,对列数的采样的占比。
subsample参数和colsample_bytree参数可以起到相同的作用,一般用不到。10.lambda[默认1]
权重的L2正则化项。(和Ridge regression类似)。
这个参数是用来控制XGBoost的正则化部分的。虽然大部分数据科学家很少用到这个参数,但是这个参数在减少过拟合上还是可以挖掘出更多用处的。11.alpha[默认1]
权重的L1正则化项。(和Lasso regression类似)。
可以应用在很高维度的情况下,使得算法的速度更快。12.scale_pos_weight[默认1]
在各类别样本十分不平衡时,把这个参数设定为一个正值,可以使算法更快收敛。
XGBoost原理粗略讲解
XGBoost底层实现了GBDT算法,并对GBDT算法做了一系列优化:
- 对目标函数进行了泰勒展示的二阶展开,可以更加高效拟合误差。
- 提出了一种估计分裂点的算法加速CART树的构建过程,同时可以处理稀疏数据。
- 提出了一种树的并行策略加速迭代。
- 为模型的分布式算法进行了底层优化。
XGBoost是基于CART树的集成模型,它的思想是串联多个决策树模型共同进行决策。
那么如何串联呢?XGBoost采用迭代预测误差的方法串联。举个通俗的例子,我们现在需要预测一辆车价值3000元。我们构建决策树1训练后预测为2600元,我们发现有400元的误差,那么决策树2的训练目标为400元,但决策树2的预测结果为350元,还存在50元的误差就交给第三棵树……以此类推,每一颗树用来估计之前所有树的误差,最后所有树预测结果的求和就是最终预测结果!
XGBoost的基模型是CART回归树,它有两个特点:(1)CART树,是一颗二叉树。(2)回归树,最后拟合结果是连续值。
1.2.2 LightGBM
相关文章推荐:基于英雄联盟数据集的LightGBM分类实战
LightGBM的主要优点:
主要改进:直方图算法:先把连续的浮点特征值离散化成k个整数
最明显就是内存消耗的降低,直方图算法不仅不需要额外存储预排序的结果
运行速度较快
LightGBM的主要缺点:
基于偏差的算法,会对噪点较为敏感
LightGBM的重要参数
基本参数调整
num_leaves参数 这是控制树模型复杂度的主要参数,一般的我们会使num_leaves小于(2的max_depth次方),以防止过拟合。由于LightGBM是leaf-wise建树与XGBoost的depth-wise建树方法不同,num_leaves比depth有更大的作用。、
min_data_in_leaf 这是处理过拟合问题中一个非常重要的参数. 它的值取决于训练数据的样本个树和 num_leaves参数. 将其设置的较大可以避免生成一个过深的树, 但有可能导致欠拟合. 实际应用中, 对于大数据集, 设置其为几百或几千就足够了.
max_depth 树的深度,depth 的概念在 leaf-wise 树中并没有多大作用, 因为并不存在一个从 leaves 到 depth 的合理映射。
针对训练速度的参数调整
- 通过设置 bagging_fraction 和 bagging_freq 参数来使用 bagging 方法。
- 通过设置 feature_fraction 参数来使用特征的子抽样。
- 选择较小的 max_bin 参数。
- 使用 save_binary 在未来的学习过程对数据加载进行加速。
针对准确率的参数调整
- 使用较大的 max_bin (学习速度可能变慢)
- 使用较小的 learning_rate 和较大的 num_iterations
- 使用较大的 num_leaves (可能导致过拟合)
- 使用更大的训练数据
- 尝试 dart 模式
针对过拟合的参数调整
- 使用较小的 max_bin
- 使用较小的 num_leaves
- 使用 min_data_in_leaf 和 min_sum_hessian_in_leaf
- 通过设置 bagging_fraction 和 bagging_freq 来使用 bagging
- 通过设置 feature_fraction 来使用特征子抽样
- 使用更大的训练数据
- 使用 lambda_l1, lambda_l2 和 min_gain_to_split 来使用正则
- 尝试 max_depth 来避免生成过深的树
2.多种模型对比
train = sample_feature[continuous_feature_names + ['price']].dropna()
train_X = train[continuous_feature_names]
train_y = train['price']
train_y_ln = np.log(train_y + 1)sklearn是基于python语言的机器学习工具包,是目前做机器学习项目当之无愧的第一工具。 sklearn自带了大量的数据集,可供我们练习各种机器学习算法。 sklearn集成了数据预处理、数据特征选择、数据特征降维、分类\回归\聚类模型、模型评估等非常全面算法。
相关文章:功能强大的python包(五):sklearn 功能介绍 推荐
2.1 线性模型 & 嵌入式特征选择【岭回归与Lasso回归】
本章节默认,学习者已经了解关于过拟合、模型复杂度、正则化等概念。否则请寻找相关资料或参考如下连接:
- 用简单易懂的语言描述「过拟合 overfitting」? -
- 模型复杂度与模型的泛化能力 呓语 | 杨英明的个人博客
- 机器学习中正则化项L1和L2的直观理解_阿拉丁吃米粉的博客-CSDN博客_l1 l2正则化
在过滤式和包裹式特征选择方法中,特征选择过程与学习器训练过程有明显的分别。而嵌入式特征选择在学习器训练过程中自动地进行特征选择。嵌入式选择最常用的是L1正则化与L2正则化。在对线性回归模型加入两种正则化方法后,他们分别变成了岭回归与Lasso回归
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
models = [LinearRegression(),
Ridge(),
Lasso()]
result = dict()
for model in models:
model_name = str(model).split('(')[0]
scores = cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error))
result[model_name] = scores
print(model_name + ' is finished')对三种方法的效果对比
result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1, 6)]
resultmodel = LinearRegression().fit(train_X, train_y_ln)
print('intercept:'+ str(model.intercept_))
sns.barplot(abs(model.coef_), continuous_feature_names)L2正则化在拟合过程中通常都倾向于让权值尽可能小,最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程,若参数很大,那么只要数据偏移一点点,就会对结果造成很大的影响;但如果参数足够小,数据偏移得多一点也不会对结果造成什么影响,专业一点的说法是『抗扰动能力强』
model = Ridge().fit(train_X, train_y_ln)
print('intercept:'+ str(model.intercept_))
sns.barplot(abs(model.coef_), continuous_feature_names)L1正则化有助于生成一个稀疏权值矩阵,进而可以用于特征选择。如下图,我们发现power与userd_time特征非常重要。
model = Lasso().fit(train_X, train_y_ln)
print('intercept:'+ str(model.intercept_))
sns.barplot(abs(model.coef_), continuous_feature_names)除此之外,决策树通过信息熵或GINI指数选择分裂节点时,优先选择的分裂特征也更加重要,这同样是一种特征选择的方法。XGBoost与LightGBM模型中的model_importance指标正是基于此计算的
2.2 非线性模型【决策树、随机森林】
除了线性模型以外,还有许多我们常用的非线性模型如下,
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.neural_network import MLPRegressor
from xgboost.sklearn import XGBRegressor
from lightgbm.sklearn import LGBMRegressor
models = [LinearRegression(),
DecisionTreeRegressor(),
RandomForestRegressor(),
GradientBoostingRegressor(),
MLPRegressor(solver='lbfgs', max_iter=100),
XGBRegressor(n_estimators = 100, objective='reg:squarederror'),
LGBMRegressor(n_estimators = 100)]
result = dict()
for model in models:
model_name = str(model).split('(')[0]
scores = cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error))
result[model_name] = scores
print(model_name + ' is finished')result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1, 6)]
result可以看到随机森林模型在每一个fold中均取得了更好的效果
3.模型调参
在此我们介绍了三种常用的调参方法如下:
- 贪心算法 五大常用算法之一:贪心算法 - 简书
- 网格调参 sklearn-GridSearchCV 网格搜索 调参数_打牛地的博客-CSDN博客_gridsearchcv sklearn
- 贝叶斯调参 自动化机器学习(AutoML)之自动贝叶斯调参_linxid的博客-CSDN博客_贝叶斯调参
3.1 贪心调参
先使用当前对模型影响最大的参数进行调优,达到当前参数下的模型最优化,再使用对模型影响次之的参数进行调优,如此下去,直到所有的参数调整完毕。
这个方法的缺点就是可能会调到局部最优而不是全局最优,但是只需要一步一步的进行参数最优化调试即可,容易理解。
需要注意的是在树模型中参数调整的顺序,也就是各个参数对模型的影响程度,这里列举一下日常调参过程中常用的参数和调参顺序:
- ①:max_depth、num_leaves
- ②:min_data_in_leaf、min_child_weight
- ③:bagging_fraction、 feature_fraction、bagging_freq
- ④:reg_lambda、reg_alpha
- ⑤:min_split_gain
best_obj = dict()
for obj in objective:
model = LGBMRegressor(objective=obj)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_obj[obj] = score
best_leaves = dict()
for leaves in num_leaves:
model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0], num_leaves=leaves)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_leaves[leaves] = score
best_depth = dict()
for depth in max_depth:
model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0],
num_leaves=min(best_leaves.items(), key=lambda x:x[1])[0],
max_depth=depth)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_depth[depth] = scoresns.lineplot(x=['0_initial','1_turning_obj','2_turning_leaves','3_turning_depth'], y=[0.143 ,min(best_obj.values()), min(best_leaves.values()), min(best_depth.values())])3.2 网格搜索GridSearchCV
sklearn 提供GridSearchCV用于进行网格搜索,只需要把模型的参数输进去,就能给出最优化的结果和参数。相比起贪心调参,网格搜索的结果会更优,但是网格搜索只适合于小数据集,一旦数据的量级上去了,很难得出结果。(GridSearchCV能够使我们找到范围内最优的参数,param_grid参数越多,组合越多,计算的时间也需要越多,GridSearchCV使用于小数据集)
GridSearchCV:一种调参的方法,当你算法模型效果不是很好时,可以通过该方法来调整参数,通过循环遍历,尝试每一种参数组合,返回最好的得分值的参数组合,比如支持向量机中的参数 C 和 gamma ,当我们不知道哪个参数效果更好时,可以通过该方法来选择参数,我们把C 和gamma 的选择范围定位[0.001,0.01,0.1,1,10,100],每个参数都能组合在一起,循环过程就像是在网格中遍历,所以叫网格搜索
from sklearn.model_selection import GridSearchCV
parameters = {'objective': objective , 'num_leaves': num_leaves, 'max_depth': max_depth}
model = LGBMRegressor()
clf = GridSearchCV(model, parameters, cv=5)
clf = clf.fit(train_X, train_y)
clf.best_params_
{'max_depth': 15, 'num_leaves': 55, 'objective': 'regression'}
model = LGBMRegressor(objective='regression',
num_leaves=55,
max_depth=15)
np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
0.13754980387410293.3 贝叶斯调参
在使用之前需要先安装包bayesian-optimization,运行如下命令即可:
pip install bayesian-optimization贝叶斯调参的主要思想是:给定优化的目标函数(广义的函数,只需指定输入和输出即可,无需知道内部结构以及数学性质),通过不断地添加样本点来更新目标函数的后验分布(高斯过程,直到后验分布基本贴合于真实分布)。简单的说,就是考虑了上一次参数的信息,从而更好的调整当前的参数。
贝叶斯优化问题有四个部分:
目标函数:我们想要最小化的内容,在这里,目标函数是机器学习模型使用该组超参数在验证集上的损失。
域空间:要搜索的超参数的取值范围
优化算法:构造替代函数并选择下一个超参数值进行评估的方法。
结果历史记录:来自目标函数评估的存储结果,包括超参数和验证集上的损失
贝叶斯调参的步骤如下:
- 定义优化函数(rf_cv)
- 建立模型
- 定义待优化的参数
- 得到优化结果,并返回要优化的分数指标
from bayes_opt import BayesianOptimization
def rf_cv(num_leaves, max_depth, subsample, min_child_samples):
val = cross_val_score(
LGBMRegressor(objective = 'regression_l1',
num_leaves=int(num_leaves),
max_depth=int(max_depth),
subsample = subsample,
min_child_samples = int(min_child_samples)
),
X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)
).mean()
return 1 - val
rf_bo = BayesianOptimization(
rf_cv,
{
'num_leaves': (2, 100),
'max_depth': (2, 100),
'subsample': (0.1, 1),
'min_child_samples' : (2, 100)
}
)
rf_bo.maximize()LightGBM中包括但不限于下列对模型影响较大的参数:
- learning_rate: 有时也叫作eta,系统默认值为0.3。每一步迭代的步长,很重要。太大了运行准确率不高,太小了运行速度慢。
- num_leaves:系统默认为32。这个参数控制每棵树中最大叶子节点数量。
- feature_fraction:系统默认值为1。我们一般设置成0.8左右。用来控制每棵随机采样的列数的占比(每一列是一个特征)。
- max_depth: 系统默认值为6,我们常用3-10之间的数字。这个值为树的最大深度。这个值是用来控制过拟合的。max_depth越大,模型学习的更加具体。
- rf_bo.max['target']plt.figure(figsize=(13,5))
sns.lineplot(x=['0_origin','1_log_transfer','2_L1_&_L2','3_change_model','4_parameter_turning'], y=[1.36 ,0.19, 0.19, 0.14, 0.13])得到结果。
-
模型调参小总结
-
集成模型内置的cv函数可以较快的进行单一参数的调节,一般可以用来优先确定树模型的迭代次数
-
数据量较大的时候(例如本次项目的数据),网格搜索调参会特别特别慢,不建议尝试
-
-
集成模型中原生库和sklearn下的库部分参数不一致,需要注意,具体可以参考xgb和lgb的官方API
xgb原生库API,sklearn库下xgbAPI
lgb原生库API, sklearn库下lgbAPI
贝叶斯详细调参过程可以参考文章:
自动化机器学习(AutoML)之自动贝叶斯调参_linxid的博客-CSDN博客_贝叶斯调参
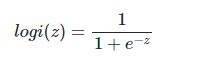
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第1张图片](http://img.e-com-net.com/image/info8/f04b2ac19b1d4b118f30769dcb1b72de.jpg)
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第2张图片](http://img.e-com-net.com/image/info8/507ea48942ac42deaf52feaf06253b98.jpg)
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第3张图片](http://img.e-com-net.com/image/info8/90fc97889ed048d4bf6c9694b9c8eb9d.jpg)
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第4张图片](http://img.e-com-net.com/image/info8/c993072c35984d10abafe25d2bd32681.jpg)
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第5张图片](http://img.e-com-net.com/image/info8/819cb9673019465aaff489f0ae093fc0.jpg)
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第6张图片](http://img.e-com-net.com/image/info8/3ee40755e26a4f6a9fc99d7f82b3d6b7.jpg)
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第7张图片](http://img.e-com-net.com/image/info8/fb913d58f9bb4f689a6d0fdd58b093f4.jpg)
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第8张图片](http://img.e-com-net.com/image/info8/10629736405c41728c409c3cba964ef0.jpg)
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第9张图片](http://img.e-com-net.com/image/info8/ed8f272dda674cec86f0a82ff2e4e793.jpg)
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第10张图片](http://img.e-com-net.com/image/info8/ee53d22e0ec84fb994ceae06102483be.jpg)
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第11张图片](http://img.e-com-net.com/image/info8/340be629c6e04ec4a5384edc0bb291d2.jpg)
![数据挖掘机器学习[四]---汽车交易价格预测详细版本{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}_第12张图片](http://img.e-com-net.com/image/info8/22c0ab2ef0204efc9c28e637c743719f.jpg)