机器学习（14）——激活函数

1 定义

  激活函数 (Activation functions) 对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到神经网络中。在下图中，输入的 inputs 通过加权，求和后，还被作用了一个函数，这个函数就是激活函数。引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后，无非还是个矩阵相乘罢了。

2 激活函数的必要性

  如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机(Perceptron)。这种情况无论有多少层神经网络均可以仅使用输入层和输出层代替，不同的地方就是线性函数的系数不同。激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

3 常用的激活函数

3.1 单位阶跃函数

  单位阶跃函数，又称赫维赛德阶跃函数，方程式如下：
$$f(x)=\{\begin{array}{ll}0,& x<0\\ 1,& x\ge 0\end{array}$$
函数曲线如下：

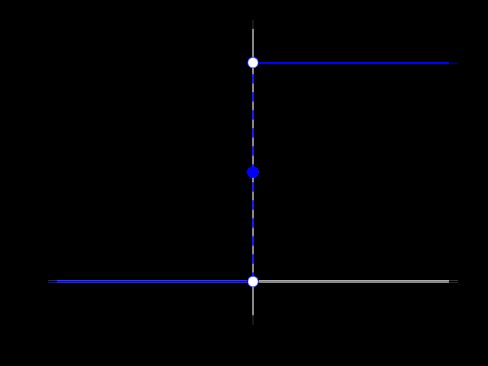
可以看出是个不连续函数，它是一个几乎必然是零的随机变量的累积分布函数，激活值只有 0 和 1，即百分百确定和百分百不确定，适合二分类问题。导数方程式如下：
$$f^{\prime }(x)=\{\begin{array}{ll}0,& x\ne 0\\ ?,& x=0\end{array}$$

3.2 Logistic函数

  Logistic 函数也叫 Sigmoid 函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，因此 Sigmoid 函数作为输出层时可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。方程式如下：
$$f(x)=\frac{1}{1+e^{-x}}$$
函数曲线如下：

其导数方程式如下：
$$f^{\prime }(x)=f(x)(1-f(x))$$
Logistic 函数平滑、易于求导，但是计算量大，反向传播求误差梯度时，求导涉及除法；反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。

3.3 Tanh函数

  Tanh 函数能够将输入“压缩”到(−1,1)区间，方程式如下：
$$f(x)=Tanh(x)=\frac{(e^x-e^{-x})}{(e^x+e^{-x})}$$
函数曲线如下：

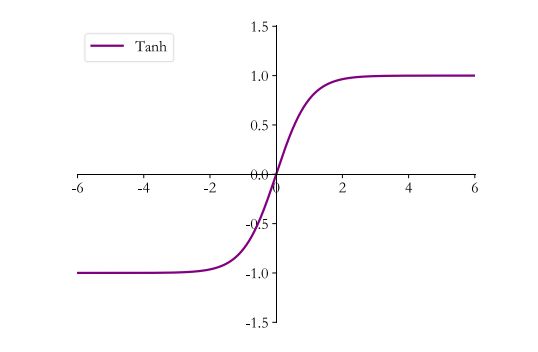
可以看到 tanh 激活函数可通过 Sigmoid 函数缩放平移后实现。其导数方程式如下：
$$f^{\prime }(x)=1-f(x{)}^2$$
与 sigmoid 函数相比，它的输出均值为0，使其收敛速度要比 sigmoid 快，可以减少迭代次数。它的缺点是需要幂运算，计算成本高；同样存在梯度消失，因为在两边一样有趋近于0的情况。

3.4 ReLU函数

  整流线性单位函数(ReLU )又称修正线性单元, 是一种人工神经网络中常用的激励函数(activation function)，通常指代以斜坡函数及其变种为代表的非线性函数。ReLU 认为有一定的生物学原理，并且由于在实践中通常有着比其他常用激励函数(譬如 Sigmoid 函数)更好的效果，而被如今的深度神经网络广泛使用于诸如图像识别等计算机视觉人工智能领域。方程式如下：
$$f(x)=max(0,x)$$
而在神经网络中，ReLU 作为神经元的激活函数，定义了该神经元在线性变换 ${\mathbf{w}}^{\mathbf{T}}+\mathbf{b}$之后的非线性输出结果。换言之，对于进入神经元的来自上一层神经网络的输入向量 $\mathbf{x}$，使用 ReLU 的神经元会输出：
$$max(0,{\mathbf{w}}^{\mathbf{T}}+\mathbf{b})$$
函数曲线如下：

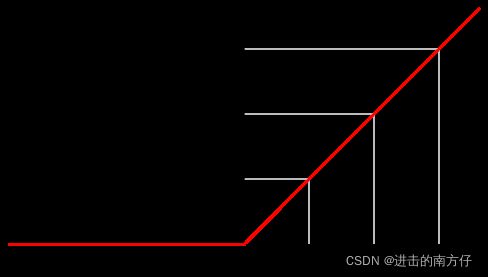
导数方程式如下：
$$f^{\prime }(x)=\{\begin{array}{ll}0,& x<0\\ 1,& x\ge 0\end{array}$$
相对 sigmoid 和 tanh，极大地改善了梯度消失的问题，收敛速度块；不需要进行指数运算，因此运算速度快，复杂度低；ReLU 函数会使得一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的互相依存关系，缓解了过拟合问题的发生。它的缺点是对参数初始化和学习率非常敏感；存在神经元死亡；ReLU 函数的输出均值大于0，偏移现象和神经元死亡会共同影响网络的收敛性。

3.5 LeakyReLU函数

  ReLU 函数在 $x<0$ 时导数值恒为 0，也可能会造成梯度弥散现象，为了克服这个问题，LeakyReLU 函数被提出，方程式如下：
$$f(x)=max(\alpha x,x)$$
其函数曲线如下：

导数方程式如下：
$$f^{\prime }(x)=\{\begin{array}{ll}1,& x\ge 0\\ \alpha ,& x<0\end{array}$$

其中 $\alpha$ 为用户自行设置的某较小数值的超参数，如 0.02 等。当 $\alpha =0$ 时，LeayReLU 函数退化为 ReLU 函数；当 $\alpha \ne 0$ 时，$x<0$ 处能够获得较小的导数值 $\alpha$，从而避免出现梯度弥散现象。

3.6 Softmax函数

  Softmax 函数，或称归一化指数函数，有多个输入，是 Sigmoid 函数的一种推广。它能将一个含任意实数的 $K$ 维向量 $\mathbf{z}$ “压缩”到另一个 $K$ 维实向量 $\mathbf{\sigma }(\mathbf{z})$ 中，使得每一个元素的范围都在(0，1)之间，并且所有元素的和为1。那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大(也就是值对应最大的)结点，作为我们的预测目标。方程式如下：
$$\mathbf{\sigma }(\mathbf{z}{)}_{\mathbf{j}}=\frac{{\mathbf{e}}^{{\mathbf{z}}_{\mathbf{j}}}}{{\sum }_{\mathbf{k}=1}^{\mathbf{K}}{\mathbf{e}}^{{\mathbf{z}}_{\mathbf{k}}}}\mathbf{for}\mathbf{j}=1,\cdots ,\mathbf{K}$$
Softmax 的使用包括两个好处，第一个好处是好求导，第二个就是它使得好结果和坏结果之间的差异更加显著，更有利于学习了。关于 Softmax 与 Loss Function 之间的求导可参考这篇文章https://zhuanlan.zhihu.com/p/25723112

4 选择恰当的激活函数

  在搭建神经网络时，如果搭建的神经网络层数不 多，选择 Sigmoid、Tanh、ReLU，LeakyReLU，Softmax 都可以；而如果搭建的网络层次较 多，那就需要小心，选择不当就可导致梯度消失问题。此时一般不宜选择 Sigmoid、Tanh 激活函数，因它们的导数都小于1，尤其是 Sigmoid 的导数在 [0,1/4]之间，多层叠加后，根据微积分链式法则，随着层数增多，导数或偏导将指数级变小。所以层数较多的激活函数需要考虑其导数不宜小于1当然 也不能大于1，大于1将导致梯度爆炸，导数为1最好，而激活函数 ReLU 及其变种正好满足这个条件。所以，搭建比较深的神经网络时，一般使用 ReLU 激活函数， 当然一般神经网络也可使用。此外，激活函数 Softmax 由于${\sum }_{\mathbf{j}=0}^{\mathbf{K}}\mathbf{\sigma }(\mathbf{z}{)}_{\mathbf{j}}=1$ 的性质，常用于多分类神经网络输出层。