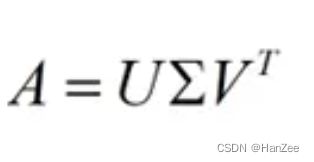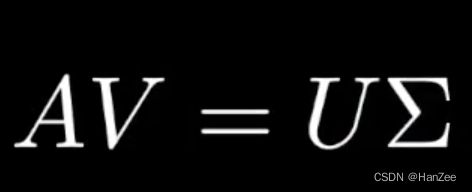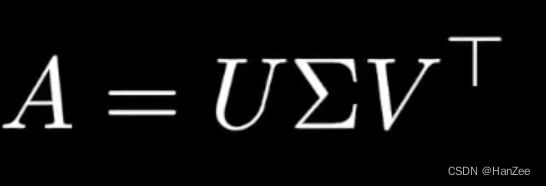机器学习：奇异值分解（SVD）详细讲解

预备知识

正交矩阵

1. 正交矩阵的每一个行向量与其他行向量相互垂直（内积=0），每一个列向量与其他列向量相互垂直。
2. 行向量或者列向量他与本身的内积=1，也就是长度=1（单位向量）。
3. 正交矩阵的逆矩阵=它的转置矩阵

逆矩阵

设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=E ，则称方阵A可逆，并称方阵B是A的逆矩阵。

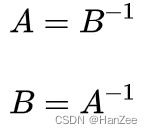
对称矩阵

对称矩阵（Symmetric Matrix）是指元素以主对角线为对称轴对应相等的矩阵，例如：

他的转置等于它本身。

对称矩阵对角化

如果一个对称矩阵是实对称矩阵，就会存在正交矩阵P，与对角矩阵满足下列等式：

然后我们对等式两边左乘P，右乘P的逆矩阵，就会得到：

又因为正交矩阵的转置=它的逆矩阵，所以对称矩阵的对角化如下：

线性变换

伸缩

一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵：

因为这个矩阵M乘以一个向量(x,y)的结果是：

旋转

除了伸缩变换，也可以进行旋转变换。

上面的矩阵是对称的，所以这个变换是一个对x，y轴的方向一个拉伸变换（每一个对角线上的元素将会对一个维度进行拉伸变换，当值>1时，是拉长，当值<1时时缩短），当矩阵不是对称的时候，假如说矩阵是下面的样子：

特征值分解

特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征的方向。
如果说一个向量v是一个方阵A的特征向量，将一可以表示成下面形式
$$Av=\lambda v$$
$\lambda$为特征向量v的特征值，特征值分解是将一个矩阵分解为如下形式：
$$A=Q\sum Q^{-1}$$
其中Q是这个矩阵A的特征向量所组成的矩阵，$\sum$是一个对角矩阵，每一个对角线元素就是一个特征值，里面的特征值有大到小排列，这些特征值所对应的特征向量就是描述这个矩阵变化方向，（从主要的变化到次要的变化排序）。也就是说矩阵A的信息可以由其特征值和特征向量表示。

对于矩阵为高纬的情况下，那么这个矩阵就是高维空间下的一个线性变换，可以想像，这个变化也同样有很多的变换方向，我们通过特征值分解得到的前N个特征向量，那就对应了这个矩阵最主要的N个变化方向，我们利用这前N个变化方向，就可以近似这个矩阵（变换）。

代码实现

import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
V, U = np.linalg.eig(A)
print(V)
print(U)

奇异值分解分解（SVD）

上面我们描述了特征值分解，但是他有一个弊端，就是被分解的矩阵只能是方阵，而SVD则可以分解任何矩阵。

SVD推导

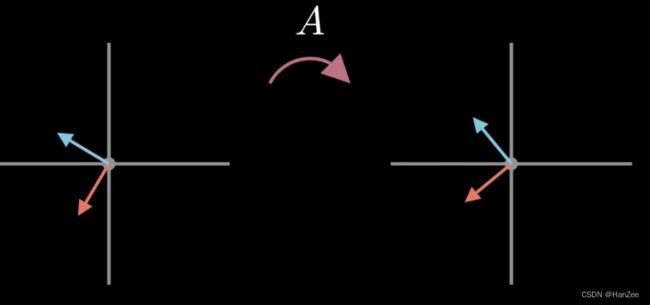
假设我们要找到一组正交的向量v1 v2，它们归一化并通过矩阵A线性变换后得到y1 ,y2,其中y1,y2继续保持正交。
就有如下公式：

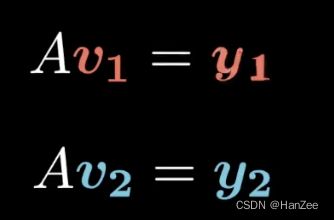
之后我们把 y1,y2写成$\sigma \ast u$其中sigma表示向量方向，u表示向量大小。

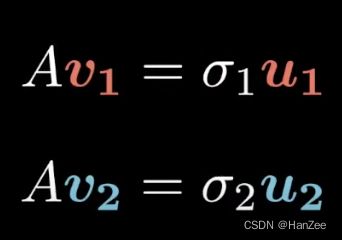
为让表达式更通用，我们把它写成矩阵的形式：

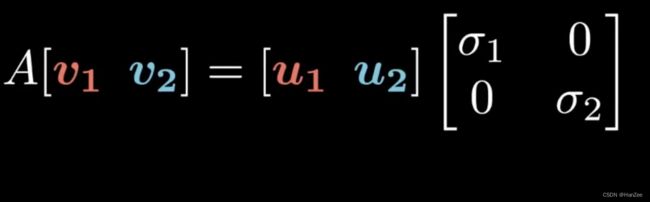
用大写字母表示：

因为V矩阵是正交矩阵，它的逆矩阵=转置矩阵，然后把等式两边同乘V的逆矩阵，就得到SVD的标准形式：

SVD计算案例

1. 计算：
   $A^T\ast A$
   $=(U\sum V^T{)}^T\ast U\sum V^T$
   $=V\sum U^{T}U\sum V^T$
   $=V{\sum }^2{V}^T$

2. $A\ast A^T$
   $=U\sum V^T\ast (U\sum V^T{)}^T$
   $=U\sum V^{T}V\sum U^T$
   $=U{\sum }^2{U}^T$

又因为A的转置乘A是对称矩阵，所以我们可以利用对称矩阵对角化，对上述结果进行特征值分解。
我们就可以计算出U、V与 ${\sum }^2$,之后在开根号，就可以得到奇异值。

SVD代码实现

import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
u,sigma,v = np.linalg.svd(A)
print(u)
print(sigma)
print(v)

SVD的应用

1. 图像压缩
2. 推荐系统
3. 图像去噪
4. 计算伪逆