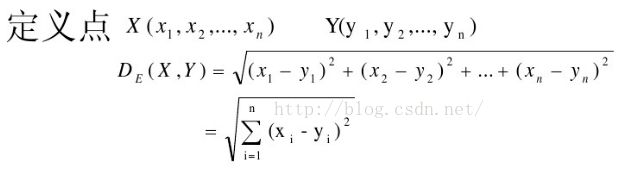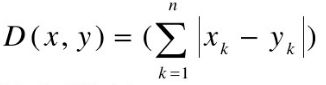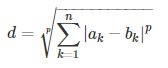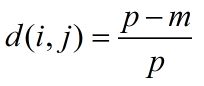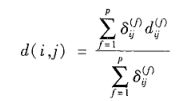数据分析 第五篇:基于距离评估数据的相似性和相异性
聚类分析根据对象之间的相异程度,把对象分成多个簇,簇是数据对象的集合,聚类分析使得同一个簇中的对象相似,而与其他簇中的对象相异。相似性和相异性(dissimilarity)是根据数据对象的属性值评估的,通常涉及到距离度量。相似性(similarity)和相异性(dissimilarity)是负相关的,统称为临近性(proximity)。
在聚类分析中,聚类算法的第一步都是度量数据集对象之间的距离,实际操作步骤是:对数据矩阵(用于存储数据对象)进行无量纲化处理,应用距离算法,得到相异性矩阵(用于存放数据对象的相异性值)。
注意:在计算距离之前,首先对数据进行无量纲化处理。
一,数据矩阵和相异性矩阵
假设我们有n个对象(如人),被p个属性(又称维或特征,如年龄、身高、体重或性别)刻画,这些对象记作x1=(x11,x12,…,x1p),x2=(x21,x22,…,x2p),等等,其中xij是对象xi的第j个属性的值,对象xi也称作对象的特征向量。把xi的集合叫做数据矩阵,各个对象之间的距离构成的矩阵,叫做相异性矩阵,通常情况下,常用的聚类算法都需要在这两种数据结构上运行。
1,数据矩阵
数据矩阵(data matrix)或称对象-属性结构:这种数据结构用关系表的形式或n×p(n个对象×p个属性)矩阵存放n个数据对象:
2,相异性矩阵
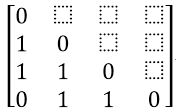
相异性矩阵(dissimilarity matrix)或称对象-对象结构:存放n个对象两两之间的邻近度(proximity),通常用一个n×n矩阵表示:
![]()
其中d(i,j)是对象i和对象j之间的相异性或“差别”的度量,一般而言,d(i,j)是一个非负的数值,对象i和j彼此高度相似或“接近”时,其值接近于0;而越不同,该值越大。注意,d(i,i)=0,即一个对象与自己的差别为0。此外,d(i,j)=d(j,i)。(为了易读性,我们不显示d(j,i),该矩阵是对称的。)
数据矩阵由两种不同类型的实体或“事物”组成,即行(代表对象)和列(代表属性)。因而,数据矩阵经常被称为二模(two-mode)矩阵。相异性矩阵只包含一类实体,因此被称为单模(one-mode)矩阵。许多聚类和最近邻算法都在相异性矩阵上运行,对于基于距离的相异性矩阵,可以使用stats包中的dist()函数把数据矩阵转换为相异性矩阵。
二,数值属性的距离度量
1,欧几里得距离
聚类算法中最常用的距离度量,表示空间中两点之间的直线距离:
由于特征向量的各分量的量纲不一致,通常需要先对各分量进行标准化,使其与单位无关,比如,对身高(cm)和体重(kg)两个单位不同的指标使用欧式距离可能使结果失效。
缺点:没有考虑分量之间的相关性,体现单一特征的多个分量会干扰结果。
2,最大距离(切比雪夫)
国际象棋玩过吗?国王走一步能够移动到相邻的8个方格中的任意一个,那么国王从格子(x1,y1)走到格子(x2,y2)上,最少需要多少步?你会发现最少步数总是max( | x2-x1 | , | y2-y1 | ) 步 。
3,曼哈顿距离
之所以如此命名,是因为它是城市两个点之间的街区距离,想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼,实际驾驶距离就是这个“曼哈顿距离”,而这也是曼哈顿距离名称的来源, 曼哈顿距离也称为城市街区距离(City Block distance),例如,向南2个街区,横过3个街区,共计5个街区。
4,兰氏距离(Lance距离)
兰氏距离克服了量纲的影响,但没有考虑指标间的相关性。
5,闵科夫斯基距离
闵科夫斯基距离需要用到参数p,
其中p是一个变参数,根据变参数的不同,闵氏距离可以表示一类的距离:
- 当p=1时,就是曼哈顿距离
- 当p=2时,就是欧氏距离
- 当p→∞时,就是最大距离
闵氏距离的缺点主要有两个:(1) 将各个分量的量纲(scale),也就是“单位”当作相同的看待了,(2) 没有考虑各个分量的分布(期望,方差等)可能是不同的。
6,马氏距离
马氏距离的优点:量纲无关,排除变量之间的相关性的干扰,缺点是:不同的特征不能差别对待,可能夸大弱特征。
适用场合:
1、度量两个服从同一分布并且其协方差矩阵为C的随机变量X与Y的差异程度
2、度量X与某一类的均值向量的差异程度,判别样本的归属。此时,Y为类均值向量.
使用R语言实现马氏距离:
dist_mashi <-function(a,b){ return (((a-b)%*% t(t(a-b))) / cov(a,b)) }
三,类别属性的相异性
类别属性(也叫做标称属性)把数据分成有限的分组,如何计算类别属性所刻画的对象之间的相异性呢?两个对象 i 和 j 之间的相异性可以根据不匹配率来计算:
其中,m是匹配的数目(即对象 i 和 j 取值相同的属性数),而p是刻画对象的属性总数,我们可以通过赋予m较大的权重来增加m的影响。
例如,包含标称属性的表,只有一个标称属性,p值等于1,设置m值为1:
当对象i和j匹配时,相异度量 d(i, j)=0,当对象i和j不匹配时,相异度量 d(i, j)=1,得到相异矩阵:
四,混合类型属性的相异性
如何计算混合属性类型的对象之间的相异性?一种更可取的方法是:把所有属性类型一起处理,把不同的属性组合到单个相异性矩阵中,把所有有意义的属性转换到共同的区间 [0.0, 1.0] 上。
假设数据集中包含p个混合类型的属性,对象i和j之间的相异性 d(i, j) 定义为:
对数值属性进行规范化处理,把变量值映射到区间[0.0, 1.0],使得所有的属性值都映射到区间[0.0, 1.0],然后再计算数值属性的距离。
五,R函数计算相异矩阵
使用R计算距离时,常用的函数是stats包中dist()和 cluster包中的daisy(),dist()用于计算数值属性的相异性矩阵,而daisy()函数用于计算(对称或非对称)二元(binary)属性、标称(nominal)属性、有序(ordinal)属性、数值属性和混合属性的相异性矩阵。
1,使用dist()函数计算相异性矩阵
stats包中的dist()函数用于计算两个数值型观测值之间的距离:
dist(x, method = "euclidean", diag = FALSE, upper = FALSE, p = 2)
该函数计算并返回通过使用指定的距离度量计算的距离矩阵,以计算数据矩阵的行之间的距离。
参数注释:
- method:度量距离的方法,默认值是"euclidean",可用的方法是:
"euclidean"、"maximum"、"manhattan"、"canberra"、"binary"和"minkowski",中文名称分别是:欧几里得、最大距离、曼哈顿、兰氏距离、二元距离和闵科夫斯基距离。 - diag:逻辑值,是否绘制距离矩阵的对角线(diagonal)
- upper:逻辑值,是否绘制距离矩阵的上三角(upper triangle)
- p:用于闵科夫斯基距离,指定power值
dist()方法返回一个下三角矩阵,使用as.matrix()函数可以使用标准中括号得到距离。
d <- dist(x) m <- as.matrix(d)
2,使用daisy()函数计算相异性矩阵
cluster包中的daisy()函数用于计算数据集中两个观测值之间的距离。当原始变量是混合类型,或者设置metric="gower"时,daisy()都会使用Gower公式计算数据集的相异型矩阵。
daisy(x, metric = c("euclidean", "manhattan", "gower"), stand = FALSE, type = list(), weights = rep.int(1, p), ...)
参数注释:
- x:数值矩阵或数据框,数值类型的变量被识别为区间缩放变量,因子类型的变量被识别为标称属性,有序因子被识别为有序变量,其他变量类型需要在type参数中指定。
- metric:字符类型,有效值是 "euclidean" (默认值)、 "manhattan" 和 "gower"。
- stand:逻辑值,在计算相异性之前是否按列对数据进行标准化
- type:list类型,用于指定x中变量的类型,有效的列表项是"ordratio" (用于序数变量),、"logratio" (用于对数转换)、"asymm" (用于非对称二元属性) 和"symm" (用于对称二元属性和标称属性).
- weights:数值向量(长度是x的列的数量 p=ncol(x)),用于混合类型的变量(或 metric="gower"),指定每个变量的权重,默认的权重是1。
函数描述:
daisy()通过使用Gower相异系数(1971)来实现对标称、序数和二元属性数据的处理。如果x的变量是标称、序数和二元类型的数据,那么函数将忽略metric和stand参数,使用Gower 系数计算数据矩阵的距离。对于纯数值数据,也可以通过设置metric="gower"来计算相异性矩阵,计算的流程是先对数据对象进行标准化,标准化的算法是:(x-min)/(max-min),把数据缩放到范围[0.0, 1.0]中。
参考文档:
数据挖掘基础:度量数据的相似性和相异性
相似性度量(距离及相似系数)
R语言:计算各种距离
数据挖掘:概念与技术--笔记1--度量数据的相似性与相异性