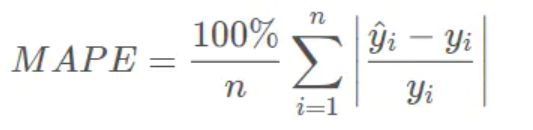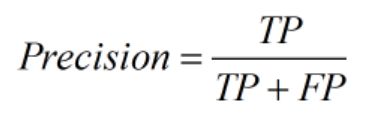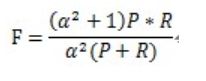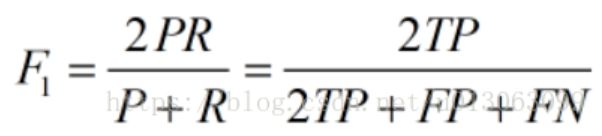机器学习-模型评估指标与计算方法

 

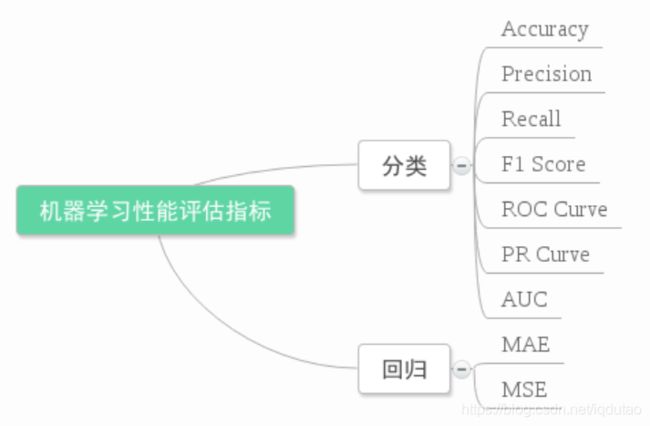
      在机器学习、数据挖掘、推荐系统完成建模之后，需要对模型的效果做评价。业内目前常常采用的评价指标有准确率(Precision)、召回率(Recall)、F值(F-Measure)等，下图是不同机器学习算法的评价指标，下文讲对其中某些指标做简要介绍。

                    

回归模型评价

回归算法的评价指标就是MSE，RMSE，MAE、R-Squared等，我们假设预测值和真实值为：

             

MSE，均方误差（Mean Square Error），取值范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

               

RMSE，均方根误差（Root Mean Square Error），其实就是MSE加了个根号，这样数量级上比较直观，比如RMSE=10，可以认为回归效果相比真实值平均相差10，范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

                

MAE，平均绝对误差（Mean Absolute Error），范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

                

MAPE，平均绝对百分比误差（Mean Absolute Percentage Error），范围[0,+∞)，MAPE 为0%表示完美模型，MAPE 大于 100 %则表示劣质模型。 可以看到，MAPE跟MAE很像，就是多了个分母。 相比RMSE，MAPE相当于把每个点的误差进行了归一化，降低了个别离群点带来的绝对误差的影响。

                

R-平方 R Squared，在讲确定系数之前，我们需要介绍另外两个参数SSR和SST，因为确定系数就是由它们两个决定的

SSR：Sum of squares of the regression，即预测数据与原始数据均值之差的平方和，公式如下:

               

SST：Total sum of squares，即原始数据和均值之差的平方和，公式如下:

                 

我们的“确定系数”是定义为SSR和SST的比值，故

                

其实“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1]，越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好

 

分类模型评价

混淆矩阵

       混淆矩阵是评判模型结果的指标，属于模型评估的一部分。此外，混淆矩阵多用于判断分类器（Classifier）的优劣，适用于分类型的数据模型，如分类树（Classification Tree）、逻辑回归（Logistic Regression）、线性判别分析（Linear Discriminant Analysis）等方法。

True Positive (真正，TP)：将正类预测为正类数

True Negative(真负，TN)：将负类预测为负类数

False Positive(假正，FP)：将负类预测为正类数误报 (Type I error)

False Negative(假负，FN)：将正类预测为负类数→漏报 (Type II error)

转义为：

        

 

1、准确率（Accuracy）

准确率计算公式为：

                    

注：准确率是我们最常见的评价指标，而且很容易理解，就是被分对的样本数(预测yes对的和预测no对的两部分)除以所有的样本数，通常来说，正确率越高，分类器越好。
       准确率确实是一个很好很直观的评价指标，但是有时候准确率高并不能代表一个算法就好。比如某个地区某天地震的预测，假设我们有一堆的特征作为地震分类的属性，类别只有两个：0：不发生地震、1：发生地震。一个不加思考的分类器，对每一个测试用例都将类别划分为0，那那么它就可能达到99%的准确率，但真的地震来临时，这个分类器毫无察觉，这个分类带来的损失是巨大的。为什么99%的准确率的分类器却不是我们想要的，因为这里数据分布不均衡，类别1的数据太少，完全错分类别1依然可以达到很高的准确率却忽视了我们关注的东西。再举个例子说明下。在正负样本不平衡的情况下，准确率这个评价指标有很大的缺陷。比如在互联网广告里面，点击的数量是很少的，一般只有千分之几，如果用acc，即使全部预测成负类（不点击）acc也有 99% 以上，没有意义。因此，单纯靠准确率来评价一个算法模型是远远不够科学全面的。

 

2、错误率（Error rate）

错误率则与准确率相反，描述被分类器错分的比例，error rate = (FP+FN)/(TP+TN+FP+FN)，对某一个实例来说，分对与分错是互斥事件，所以accuracy =1 - error rate。

 

5、精确率、精度（Precision）查准率。即正确预测为正的占全部预测为正的比例。个人理解：真正正确的占所有预测为正的比例。

                    

6、召回率（Recall），查全率。即正确预测为正的占全部实际为正的比例。个人理解：真正正确的占所有实际为正的比例。

                     

 

示例1: 地震的预测对于地震的预测，我们希望的是Recall（召回率/查全率） 非常高，也就是说每次地震我们都希望预测出来。这个时候我们可以牺牲Precision （精确率/查准率），情愿发出1000次警报，把10次地震都预测正确了；也不要预测100次对了8次漏了两次。

 

7、综合评价指标（F-Measure）
P和R指标有时候会出现的矛盾的情况，这样就需要综合考虑他们，最常见的方法就是F-Measure（又称为F-Score）。
F-Measure是Precision和Recall加权调和平均：

              

当参数α=1时，就是最常见的F1，也即

               

公式转化之后为：

            

可知F1综合了P和R的结果，当F1较高时则能说明试验方法比较有效。

 

8、其他评价指标

计算耗时：分类器训练和预测需要的时间；

鲁棒性：处理缺失值和异常值的能力；

可扩展性：处理大数据集的能力；

可解释性：分类器的预测标准的可理解性，像决策树产生的规则就是很容易理解的，而神经网络的一堆参数就不好理解，我们只好把它看成一个黑盒子。

 

ROC曲线：
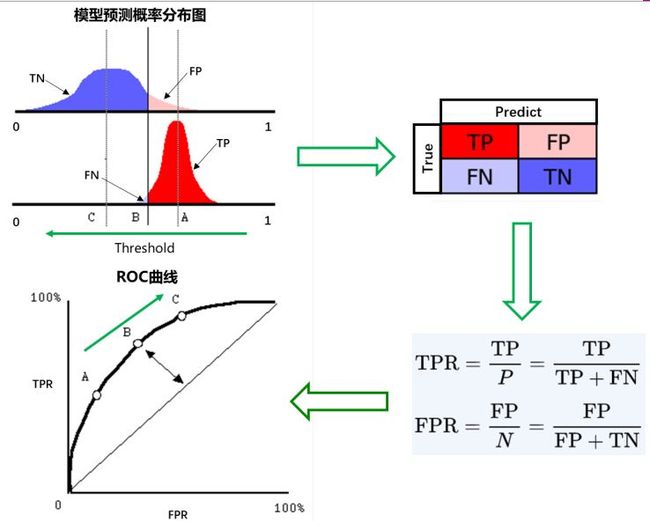
ROC（Receiver Operating Characteristic）曲线是以假正率（FP_rate）和真正率（TP_rate）为轴的曲线，ROC曲线下面的面积我们叫做AUC，如下图所示：

                           

横坐标：1-Specificity，伪正类率(False positive rate，FPR，FPR=FP/(FP+TN))，预测为正但实际为负的样本占所有负例样本的比例；

纵坐标：Sensitivity，真正类率(True positive rate，TPR，TPR=TP/(TP+FN))，（就是召回率/查全率）预测为正且实际为正的样本占所有正例样本的比例。

                 

在一个二分类模型中，假设采用逻辑回归分类器，其给出针对每个实例为正类的概率，那么通过设定一个阈值如0.6，概率大于等于0.6的为正类，小于0.6的为负类。对应的就可以算出一组(FPR，TPR)，在平面中得到对应坐标点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大。阈值最大时，对应坐标点为(0,0)，阈值最小时，对应坐标点(1,1)。真正的理想情况，TPR应接近1，FPR接近0，即图中的（0,1）点。ROC曲线越靠拢A（0,1）点，越偏离45度对角线越好。
 

AUC (Area Under Curve) 值

AUC被定义为ROC曲线下的面积，即上图中L2曲线和B点之间的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于DC这条直线的上方，所以AUC的取值范围一般在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。

从AUC判断分类器（预测模型）优劣的标准：

AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。
一句话来说，AUC值越大的分类器，正确率越高。
三种AUC值示例：

               

 

为什么使用ROC曲线

既然已经这么多评价标准，为什么还要使用ROC和AUC呢？因为ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线的对比：

                    

(a)和(c)为ROC曲线，

(b)和(d)为Precision-Recall曲线。

(a)和(b)展示的是分类器在原始测试集（正负样本分布平衡）的结果，

(c)和(d)是将测试集中负样本的数量增加到原来的10倍。（正负样本分布不均衡）

可以明显看出，ROC曲线基本保持原貌，而Precision-Recall曲线则变化较大。这个特点让ROC曲线能够尽量降低不同测试集带来的干扰，更加客观地衡量模型本身的性能。

PR曲线会面临一个问题，当需要获得更高recall时，model需要输出更多的样本，precision可能会伴随出现下降/不变/升高，得到的曲线会出现浮动差异（出现锯齿），无法像ROC一样保证单调性。所以，对于正负样本分布大致均匀的问题，ROC曲线作为性能指标更鲁棒。

                 

示例2 ：

 

 

 

 

示例3 ：

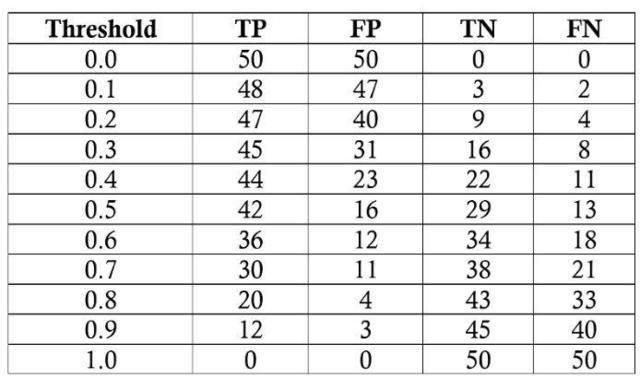
我们的任务是为 100 名病人诊断一种在普通人群中患病率是 50% 的疾病。我们将假设一个黑盒模型，我们输入关于患者的信息，并得到 0 到 1 之间的分数。我们可以改变将患者标记为正例 (有疾病) 的阈值，以最大化分类器性能。我们将以 0.1 为增量从 0.0 到 1.0 评估阈值，在每个步骤中计算 ROC 曲线上的精度、召回率、F1 score 以及在 ROC 曲线上的位置。以下是每个阈值的分类结果：

                       

我们将以阈值为 0.5 为例计算对应的召回率、精度、真正例率、假正例率，首先我们得到混淆矩阵：

                    

我们可以利用混淆矩阵中的数值来计算召回率、精度和 F1score：

然后计算真正例率和假正例率来确定阈值为 0.5 时，模型在 ROC 曲线上对应的点。为了得到整个 ROC 曲线，我们在每个阈值下都进行这个过程,最终的 ROC 曲线如下所示，点上面的数字是阈值。

                

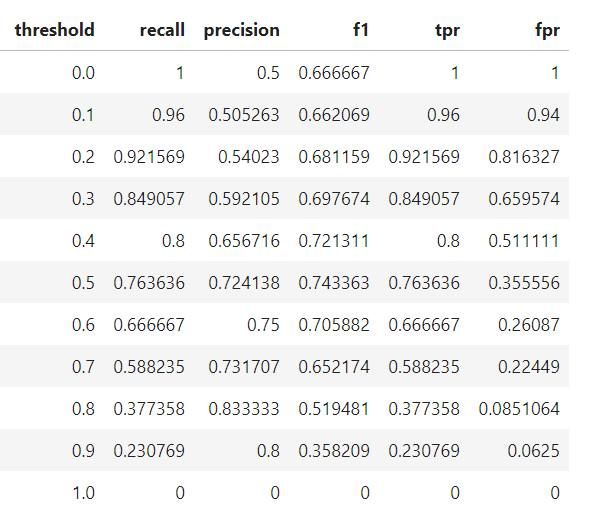
在这里我们可以看到，所有的概念都汇集到一起了！在阈值等于 1.0 的点，我们没有将任何病人归类为患病，因此模型的召回率和精度都是 0。随着阈值的减小，召回率增加了，因为我们发现更多的患者患有该疾病。然而，随着召回率的增加，精度会降低，因为除了增加真正例之外，还会增加假正例。在阈值为 0.0 的时候，我们的召回率是完美的——我们发现所有的患者都患有这种疾病——但是精度很低，因为有很多假正例。通过更改阈值并选择最大化 F1 score 的阈值，我们可以沿着给定模型的曲线移动。要改变整个曲线，我们需要建立一个不同的模型.在每个阈值下最终模型的统计量如下表：

                  

基于 F1 score，整体最佳的模型出现在阈值为 0.5 的地方。如果我们想要在更大程度上强调精度或者召回率，我们可以选择这些指标上最佳时对应的模型。

        我们倾向于使用准确率，因为每个人都知道它意味着什么，而不是因为它是完成任务的最佳工具！虽然更适合的度量指标 (如召回率和精度) 看起来可能很陌生，但我们已经直观地了解了为什么它们在某些问题 (如不平衡的分类任务) 中有着更好的表现。统计学为我们提供了计算这些指标的形式化定义和方程。数据科学是关于寻找解决问题的正确工具的学科，而且在开发分类模型时，我们常常需要超越准确率（accuracy）的单一指标。了解召回率、精度、F1 score 和 ROC 曲线使我们能够评估分类模型，并应使我们怀疑是否有人仅仅在吹捧模型的准确率，尤其是对于不平衡的问题。正如我们所看到的，准确率（accuracy）并不能对几个关键问题提供有用的评估，但现在我们知道如何使用更聪明的衡量指标！

 

 KS(Kolmogorov-Smirnov)

KS曲线是用来衡量分类型模型准确度的工具。KS曲线与ROC曲线非常的类似。其指标的计算方法与混淆矩阵、ROC基本一致。它只是用另一种方式呈现分类模型的准确性。KS值是KS图中两条线之间最大的距离，其能反映出分类器的划分能力。KS值是在模型中用于区分预测正负样本分隔程度的评价指标，一般应用于金融风控领域。

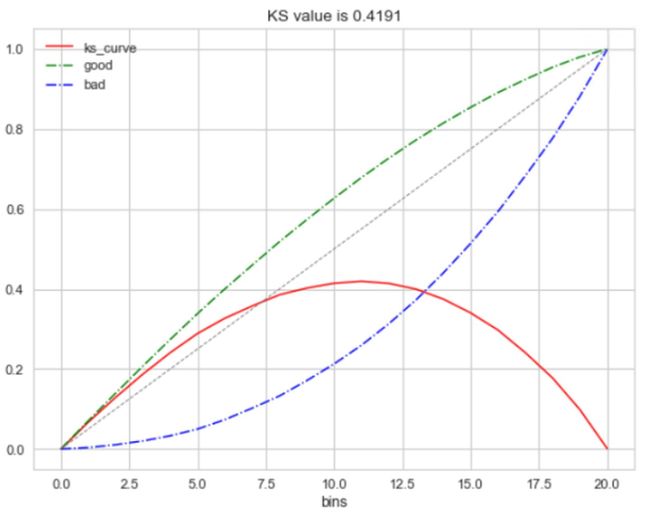
KS曲线是两条线，其横轴是阈值，纵轴是TPR与FPR。两条曲线之间之间相距最远的地方对应的阈值，就是最能划分模型的阈值。KS值是MAX(TPR - FPR），即两曲线相距最远的距离。
为什么这样求KS值呢？我们知道，当阈值减小时，TPR和FPR会同时减小，当阈值增大时，TPR和FPR会同时增大。而在实际工程中，我们希望TPR更大一些，FPR更小一些，即TPR-FPR越大越好，即ks值越大越好。

可以理解TPR是收益，FPR是代价，ks值是收益最大。图中绿色线是TPR、蓝色线是FPR。

                

ks值<0.2,一般认为模型没有区分能力。

ks值[0.2,0.3],模型具有一定区分能力，勉强可以接受

ks值[0.3,0.5],模型具有较强的区分能力。

ks值大于0.75，往往表示模型有异常。

 

 

 

参考链接：https://blog.csdn.net/u013063099/article/details/80964865
参考链接：https://zhuanlan.zhihu.com/p/41832024
参考链接：https://blog.csdn.net/quiet_girl/article/details/70830796
参考链接：https://www.jianshu.com/p/feaf14df5055