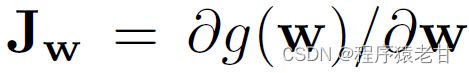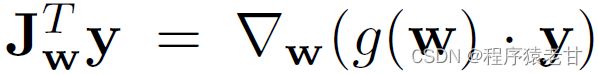GAN网络系列博客(二):改善StyleGAN的图像质量
在上一篇博客中,我们已经介绍了StyleGAN的基本实现。其主要通过间接隐空间映射,消除了对初始输入分布的硬性约束,能够比较灵活的迁移不同的风格到生成器的各层中。但是,该项工作生成的人脸图像,仍然存在一些不稳定的情况,其图像质量以及语义结构不能被保证。为了解决该问题,StyleGAN2[1]被提出。衔接上一篇博客,在本文中我们来介绍下StyleGAN2的基本原理与实现。
1. 简介
StyleGAN被证明在风格迁移任务中具有非常出色的性能,然而,其生成的图像具有一些 "characteristic artifacts"(不知道怎么翻译,大概是人工编辑痕迹的意思)。StyleGAN2主要就是用来移除这些artifacts的,具体的改良方法包括:重新设计了生成器中的归一化操作;使用progressive growing[2]来稳定高分辨率图像输出的质量。同时,StyleGAN2引入了一些图像度量方法[3][4],来进一步提高生成图像质量。文章主体包括的几个部分,刚好对应改良方法的几点。接下来,我们就来展开看看StyleGAN2针对artifacts的具体改良措施。
2. 移除Artifacts
如上所述,StyleGAN2的一个任务是用来消除StyleGAN产生的artifacts。这里列出正文中介绍的一种artifacts,即water droplets(水滴状噪声),如下图所示:
作者解释说,类似这样的artifacts,理论说应该在StyleGAN的生成器中能够避免。有可能出现问题的地方是AdaIN operation中的normalizes,即分别归一化均值与方差的特征图。
在之前的styleGan中我们已经知道,AdaIN是一步非常重要的计算,包含normalization和modulation两步。这使得我们可以包装一个style block来对应激活一种风格,如下图:
图(a)为原始的styleGAN的基本解构,图(b)为对其展开后的结果,可以看到,对应不同的中间隐空间仿射变换wi,不同的style block激活了对应的风格。有趣的是,在生成器中加入的偏差与噪声,与对应的迁移风格强度是成反比的。因此,styleGAN2把偏差与噪声的加入,移出style block执行。如果按照之前的推论,那么风格迁移的质量会被加强。经过style block的运算,偏差与噪声直接施加在标准差上,也能够满足需求。 如图(c),B输入被移除出style block。
StyGAN能够通过输入隐空间中不同的w到在不同的生成器层,以实现混合风格。但是在实践中,风格的权重不好把握(原文称有些特征会被放大几个数量级)。显然,这种放大需要被抑制。回到图(c),modulation基于传入样式缩放卷积的每个输入特征映射,被下面公式实现:
si为对应属兔的特征图的尺度变换。这里作者提出一个demodulation的方法,其目的是在实质上移除si对卷积输出特征映射的统计影响。这里假设输入的激活随机变量具有单位标准差。我们可以计算出经过调试和卷积后,输出激活的标准差为:
基于计算的标准差,只需要在后续的normalization中,按照比例算回单位标准差即可:
新的设计很好的消除了characteristic artifacts,同时保持了风格混合的灵活性。
3. 图像质量评价
针对生成的图像进行质量评价,对于改善GAN生成器十分重要。虽然已经存在FID [3],Precision [4] 或者Recall [5] 等方法来度量GAN的性能,但是仍然会留下一些视觉盲点。作者观察到图像质量与感知路径长度PPL [2] 存在关联。PPL是一种度量,最初被用来量化从潜在空间到输出图像的映射的平滑性。PPL通过测量在生成图像之间,隐空间内的小扰动的平均LPIPS距离 [6] 来质量评价。作者在文中提到,目前还不清楚为什么PPL能够对应图像质量。一个假设是在训练过程中,正如判别器惩罚破碎图片那样,生成器可通过有效的拉伸隐空间以产生高质量图片。这会导致低质量图片被压缩在一个更小的隐空间区域。
基于优化PPL以提升图像质量这个思路,作者提出了一个新的正则化用于平滑生成器映射,并避免了单纯最小化PPL而产生的零召回退化解。通过在图像空间探查关于固定步长,不同方向的w变化来估算其梯度。对于一个w,生成器映射的局部度量缩放性质g(w):W->Y被Jacobian矩阵来捕获:
为了保持期望的与方向无关的向量长度,正则化被表示为:
y表示随机的图像,像素强度符合正态分布。w~f(z),z是正态分布的。作者在附录解释了,当Jacobian矩阵对于任意w是正交时,先验能量获得最小化。一个正交的矩阵保持了长度,并不产生向任何方向的挤压。为了避免显式计算雅可比矩阵,作者使用:
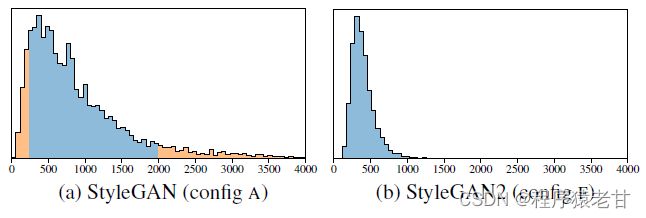
该计算能够被标准的后向传播计算 [7]。常数a在优化过程中被设置为动态的,作为长时间运行下增长的长度变换平均距离||J^T_wy||_2,进而允许优化通过自身找到一个合适的全局尺度。作者提到,所提出的正则化器与Jacobian夹逼正则化 [8] 密切相关,区别主要是关于J^T_wy的计算。在实践中,路径长度正则化能够推出更可靠且行为一致的模型,使得对架构的探索更简单。数据证明,路径长度正则化明显收紧了每张图像PPL分数的分布,如下图中的右子图所示:
在之后,作者还给出了高分辨率图像合成技术Progressive growing。但是我认为已经不是StyGAN2的核心技术了,这里我就不再赘述了,有兴趣的同学可以看下参考文献 [9]。
总结:
StyGAN2相对StyGAN的提升主要是发现了artifacts与偏差与噪声输入的关系。通过重新设置了style block的结构,将偏差与噪声输入移出style block,进而很大程度上解决了artifacts的问题。同时,通过对StyGAN正则化技术的探索以及高分辨图像输出的相关研究,建立了可行的算法框架,使得StyGAN2生成的图片,其内容的一致性,图像质量以及分辨率,都有了很大的提升。
Reference
[1] Karras T, Laine S, Aittala M, et al. Analyzing and improving the image quality of stylegan[C]. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2020: 8110-8119.
[2] Tero Karras, Timo Aila, Samuli Laine, and Jaakko Lehtinen. Progressive growing of GANs for improved quality, stability, and variation. CoRR, abs/1710.10196, 2017.
[3] Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, and Sepp Hochreiter. GANs trained by a two time-scale update rule converge to a local Nash equilibrium. In Proc. NIPS, pages 6626–6637, 2017.
[4] Mehdi S. M. Sajjadi, Olivier Bachem, Mario Lucic, Olivier Bousquet, and Sylvain Gelly. Assessing generative models via precision and recall. CoRR, abs/1806.00035, 2018
[5] Tim Salimans and Diederik P. Kingma. Weight normalization:A simple reparameterization to accelerate training of deep neural networks. CoRR, abs/1602.07868, 2016.
[6] Richard Zhang, Phillip Isola, Alexei A. Efros, Eli Shechtman, and Oliver Wang. The unreasonable effectiveness of deep features as a perceptual metric. In Proc. CVPR, 2018.
[7] Yann N. Dauphin, Harm de Vries, and Yoshua Bengio. Equilibrated adaptive learning rates for non-convex optimization. CoRR, abs/1502.04390, 2015. 5
[8] Augustus Odena, Jacob Buckman, Catherine Olsson, et al. Is generator conditioning causally related to GAN performance? CoRR, abs/1802.08768, 2018. 5.
[9] Animesh Karnewar and Oliver Wang. MSG-GAN: multiscale gradients for generative adversarial networks. In Proc. CVPR, 2020. 6