Python机器学习教程—数据预处理(sklearn库)

目录

一、前言

二、数据预处理方法原理及api调用

1.均值移除

2.范围缩放

3.二值化

4.归一化

5.独热编码

---

一、前言

了解了机器学习的基础知识后我们便正式进入机器学习的实践领域，通过实践来了解机器学习到底都在做些什么，首先要进行的一项重要工作便是数据预处理。日常生活中的数据有文字、图像、音频等多种形式，但熟悉计算机的同学都知道它们在计算机中会以01二进制的形式存在。那么以后在机器学习中最常接触的便是“一行一样本、一列一特征”的数据样本矩阵。

一般情况下利用python的sklearn库来解决数据预处理、构建机器学习模型包括模型评估的问题，所有预处理的api基本都在这个库中，这个模块也会是我们知道对当前的一组数据都有什么样的预处理手段和api方法。很常见的一个例子比如我们拿到一组数据如下图，发现有很多列是字符串，这是不利于机器学习模型的数据，我们便需要将其数字化，比如性别女设为0，男设为1。这就是预处理的一种，包括标准化、范围缩化等方式都属于预处理，也都能由这个库解决。

图1.样本数据实例

数据预处理便是是数据变得有利于机器学习模型的训练。直接拿到的数据往往无法直接拿来训练，因此数据预处理很有必要。当然这里先讲进行预处理的手段和方法。因此在接下来所学的一系列数据预处理的方法都只是教给我们怎么去用，但具体什么时候适合用目前作为初学者还很难感受到，当学习到一定程度，对机器学习有所感悟便能够有所感觉在哪些地方应该用什么样的与处理方式，这需要经验的累积。

在解决机器学习问题的时候我们需要调用的工具包，也建议写在python程序的最前面。

# 解决机器学习问题的科学计算工具包
import sklearn.preprocessing as sp
import numpy as np 
# 涉及图像的应用和处理需要
import matplotlib.pyplot as plt

二、数据预处理方法原理及api调用

1.均值移除

由于一个样本的不同特征值差异较大，不利于使用现有机器学习算法进行样本处理。均值移除可以让样本矩阵中的每一列的平均值为0，标准差为1。可能很多人会怀疑这样做的意义，这个方法确实会对数据有一定的破坏，但其是有益于增加某些机器学习的速度。调用方法如下:

# 均值移除api调用方法
# 解决机器学习问题的科学计算工县包
import sklearn.preprocessing as sp
# scale函数用于对函数进行预处理，实现均值移除。
# array为原数组，返回A为均值移除后的结果。
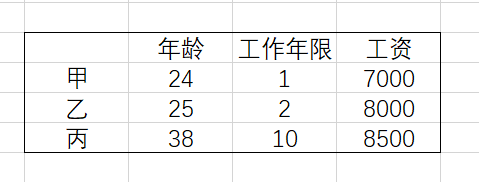
A=sp.scale(array)

接下来举个具体的例子:从样本数据可得现有三个人，根据数据可得比如甲年龄24岁，工作时长为1年，工资为7000，那么乙从数据上来看跟第一个人近似，但这样的一组数据，每个人前两列相差的量级根本无法跟第三列相比，根据实际生活经验我们可知工资8500和8000相差不算多，但年龄38和25相差不小，但这样的差值却远比不上工资在数值上的相差。这说明每个人的误差会受到相对不是那么重要的工资数值的影响。我们要尽力消除这个影响。

图2.示例数据样本

# 示例
import numpy as np 
import sklearn. preprocessing as sp 
# 每个数字后加.防止报异常
data = np.array([[24.,1.,7000.], [25.,2.,8000.], [38.,10.,8500.]]) 
result=sp.scale(data)
print(result)

# 检验每列的均值和标准差是否为0和1
print(r.mean(axis=0))# axis=0表示对列进行操作
print(r.std(axis=0))

 图3.示例结果和检验结果

2.范围缩放

这个方法会调用mms对象的fit_transform方法将样本矩阵中的每一列的最小值和最大值设定为相同的区间，统一各列特征值的范围。一般情况下会把特征值缩放至[0,1]区间。比如说我们将上面的样本矩阵中的年龄/薪水/工作年限这种特征的列中的每一个值都归到一个[0,1]的区间中。

针对这个fit_transform()方法还要强调的是，fit是训练，transform是转换，整个方法的原理便是将一列的最大值设为1，最小值设为0，其余数值均范围缩放。其实相当于有了最大值最小值两个点，确定了一条y=k×x+b的直线，其余数值均带入就能得到对应的结果。

# 范围缩放api调用方法
# 创建MinMax缩放器
mms=sp.MinMaxScaler(feature_range=(0,1))
# 调用mms对象的方法执行缩放操作，返回缩放过后的结果
result=mms.fit_transform(原始样本矩)

 仍然采用之前的样本矩阵进行示例

# 示例
"""
首先创建对象之后调用方法来对我们的数据矩阵进行操作，可由结果看出将一列的最大值设为1，
最小值设为0，其余数值则进行相应等比例的缩放。
"""
mms=sp.MinMaxScaler(feature_range=(0,1))
result=mms.fit_transform(data)
result

 图4.示例结果

3.二值化

有些业务并不需要分析矩阵的详细完整数据（比如图像边缘识别只需要分析出图像边缘即可），可以根据一个事先给定的阈值，用0和1表示特征值不高于或高于阈值。二值化后的数组中每个元素非0即1，达到简化数学模型的目的。

即整个方法的思想，就是将矩阵中所有的元素变为只有0和1这两个值的模式，因此需要设立一个阈值也可理解为临界值，元素高于临界值就被设为1，其他情况则为0。举个例子，我们在进行图像识别的时候，有时候图像很复杂，像素点很多且有很多细节。但有时候我们并不需要太复杂的细节，比如我们人便可以通过简笔画识别出一个物件，那么计算机也需如此，这也是便于其减轻负担。

# 二值化api调用
# 给出湿值，获取二值化器
bin=sp.Binarizer(threshold=阈值)
# 调用transform方法对原始样本矩阵进行二值化预处理操作
result=bin.transform(原始样本矩阵)

仍采用之前的样本矩阵进行示例 

# 设定阈值为30 矩阵元素>30变为1，否则变为0
bin=sp.Binarizer(threshold=30)
result=bin.transform(data)
print(result)

 图5.示例结果

补充一下，其实二值化的数据处理方法在图像处理领域应用较多，比如进行图像识别，有时候只需对其大致轮廓进行判断。比如我们识别下面这个机器人：

import cv2 as cv
import matplotlib.pyplot as plt
img=cv.imread('ml.jpg',0)# 读取图像为灰度图 img为图像矩阵
print(img.shape)
plt.imshow(img,cmap='gray')

图6.读取灰度图 

# 进行二值化处理
bin=sp.Binarizer(threshold=127)
result=bin.transform(img)
plt.imshow(result,cmap='gray')

图7.二值化处理后 

从图像可以看到原来机器人的大致轮廓，01相间的位置便是轮廓，因此对这样的图像要去识别我们不一定需要处理前的图像那么复杂的细节，有个轮廓我们也能看出这是机器人。这也展示着二值化的操作在图像处理中有很多应用。 

4.归一化

有些情况每个样本的每个特征值具体的值并不重要，但是每个样本特征值的占比更加重要。归一化即是用每个样本的每个特征值除以该样本各个特征值绝对值的总和。变换后的样本矩阵，每个样本的特征值绝对值之和为1。用通俗的话来说，数值矩阵中一行为一个样本，一列为一个特征，那么每个特征值/一行中所有特征值的和便是占比

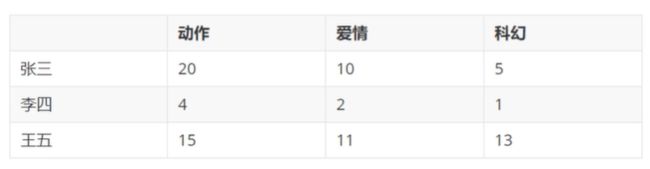
比如我们观察下面的矩阵，张三李四王五三个人看电影的类型和数量，那么我们怎么判断哪两个人看电影的口味比较相似呢？有一种可能的分析师张三和王五比较像，因为他们看的动作片都比较多（10部以上）；但另一个角度，横向来说张三看的电影中动作片最多，而李四也是动作片最多，王五虽然也是，但其对科幻片的兴趣大于爱情片，与前两人却不同。从业务逻辑上分析观影偏好，我们需要科学计算每个人观影特点之间的距离，便从观影比例入手。

图8.样本矩阵

# 归一化api调用
# array 原始样本矩阵
# norm范数
# L1范数，向量中个元素绝对值之和
# L2范数，向量中个元素平方之和
# 返回归一化预处理后的样本矩阵
sp.normalize(array,norm='l1')

下面对示例样本矩阵进行归一化操作 

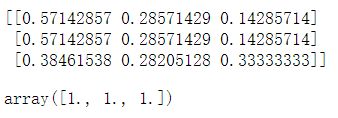
# 归一化示例
data2=np.array([[20,10,5],[4,2,1],[15,11,13]])
result=sp.normalize(data2,norm='l1')
print(result)

# 计算一下每行的绝对值之和验证其是否为1
np.abs(result).sum(axis=1)

图9.示例输出（上方为归一化后的样本矩阵，下方为每行绝对值之和检验）

5.独热编码

为样本特征的每个值建立一个由一个1和若干个0组成的序列，用该序列对所有的特征值进行编码。

如下面这个例子，由上面的四行三列矩阵进行编码，比如把第一列的1编为10，7编为01；第二列就把3作为100，5-010，8-001，类似的第四行也是如此。每一列每个数字都有编码规则，那么就开始替换变成了最下面的样本矩阵，每行都由01组成。这样的数据处理方法把原本数据比较复杂的矩阵转换为非0即1的矩阵，会在针对某些算法时变得非常有助力，还需要我们进行跟深入的学习才能体会到。

• 两个数 三个数 四个数
• 1 3 2
• 7 5 4
• 1 8 6
• 7 3 9
• 为每一个数字进行独热编码：
• 1-10 3-100 2-1000
• 7-01 5-010 4-0100
• 8-001 6-0010
• 9-0001
• 编码完毕后得到最终经过独热编码后的样本矩阵：
• 101001000
• 010100100
• 100010010
• 011000001

# 独热编码api调用
# 创建一个独热编码器
# sparse：是否使用紧缩格式（稀疏矩阵）
# dtyle：数据类型
ohe=sp.OneHotEncoder(sparse=是否采用紧缩格式,dtype=数据类型)
# 对原始样本矩阵进行处理，返回独热编码后的样本矩阵。
result=ohe.fit_transform(原始样本矩阵)

ohe=sp.oneHotEncoder(sparse=是否采用紧缩格式,dtype=数据类型)
#对原始样本矩阵进行训练，得到编码字典
encode_dict =ohe.fit(原始样本矩阵)
# 调用encode_dict字典的transform方法对数据样本矩阵进行独热编码
result=encode_dict.transform(原始样本矩阵)

对上文所举例子进行演示

# 独热编码示例
data3=np.array([[1,3,2],[7,5,4],[1,8,6],[7,3,9]])
print(data3)
ohe=sp.OneHotEncoder(sparse=False)# sparse是要确定是否采用稀疏矩阵的存储形式
result=ohe.fit_transform(data3)
print(result)

 图10.示例结果