数据库索引简介
因为也不是专门的数据库开发,或是DBA,就是针对网上的一些资料的学习总结,谬误之处难免,请网友不吝指教。
什么是索引?
简单的用字典的检索目录做比喻多少有一点事实而非,索引的结构实际上也影响了数据实体本身的存储结构,所以更细致一点说,没有索引,有索引,有聚集索引,有非聚集索引是数据库表的不同的存储,使用的方式。
关于B-Tree
要理解索引,就不能不了解他的实现。常见的实现多是用B-Tree或是B+Tree,这里简单说下我对B-Tree的理解。
B-Tree不同于Binary Tree(二叉树,最多有两个子树),一棵M阶的B-Tree满足以下条件:
1)每个结点至多有M个孩子;
2)除根结点和叶结点外,其它每个结点至少有M/2个孩子;
3)根结点至少有两个孩子(除非该树仅包含一个结点);
4)所有叶结点在同一层,叶结点不包含任何关键字信息;
5)有K个关键字的非叶结点恰好包含K+1个孩子;
上面是严格的定义,简单来说就是一棵多路搜索树。一般的二叉树,其性能在平衡的情况下,逼近二分查找。其最大的问题是,如果节点非常多,就需要大量的磁盘IO,这往往会成为系统的瓶颈。解决方案之一就是,在每个节点上多存储几个key,当然这样自然会使得算法变得更加复杂,内容的消耗也更大。但是相比于磁盘IO的龟速,cpu和内存的牺牲是可以接受的,看下面这张图,是B-Tree(M=4)的样例:
图上数字是每个节点的key数组,箭头代表指针数据,因为是4阶树,所以最多有3个key和4个子节点。查找的顺序是按照顺序,当然如果key非常多也可能用二分查找,以查找7为例,程序发现是在根节点的4和10之间,所以使用第二个指针,依次遍历6,7。发现则返回节点指针,如果到叶节点还没找到,则返回失败。
再来看看B-树的建立,M=4,依次插入1~6。从图中可以看出,当我们插入关键字4时,由于原结点已经满了,故进行分裂,基本按一半的原则进行分裂,然后取出中间的关键字2,升级(这里是成为根结点)。其它的依类推,就是这样一个大概的过程。
是不是建立索引就能提高性能?
先不说索引的实现方式和细节,先说说是不是建立索引一定能提高数据库的性能。没有“银弹”,这是技术领域的铁则,索引你可以理解为建立额外的数据用于提高查找数据的速度,但是一旦需要增删改数据,索引本身也是需要更新的。说白了读数据的提高是以写数据的性能降低作为前提的。所以数据量不是太大,或是更新非常快的字段是不适合做索引的,同样的如果字段的数据大部分相同,也不适合做索引,很好理解,大部分相同了,遍历也慢不到哪里去。
聚集索引的实现
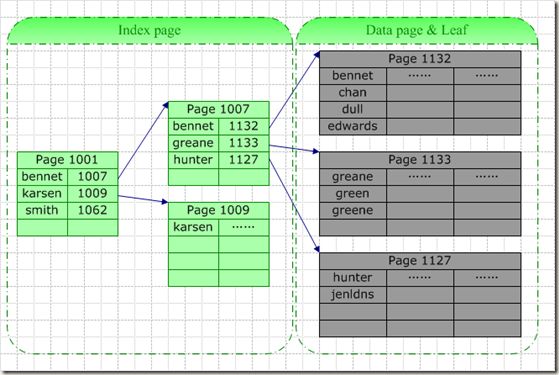
最大的特点在于叶节点就是数据节点,也就是说表与索引共同构成了一棵B-tree,这意味着数据的存储是有顺序的,比如你的年龄字段,在物理上就是顺着链表按照比如10,20,30,31这样的顺序排的,看下面的图,注意data page里的名字,是按照字母顺序排的,也就是你用select 不加order by name,它出来的也是顺序的:
具体的不多说了,图已经很明白了,名字作为索引,按照字母序作为key的顺序,索引和数据构成整个一棵树。
聚集索引的优缺点
优点就是缺点,事物的两面性尽显无疑。物理上的有序,使得范围的查询变得非常高效,比如你要查找一个日期范围,如果本身是有序的,只要找到开始和结束日期,其他的就不用找了。缺点的也是一样,为了维护这棵B-tree始终正确,必须在更新key的数据后,做出大量的调整,极端下如果key完全不相同,比如单调递增,即使更新一小批数据,也可能引起很大的延迟。
什么是非聚集索引?
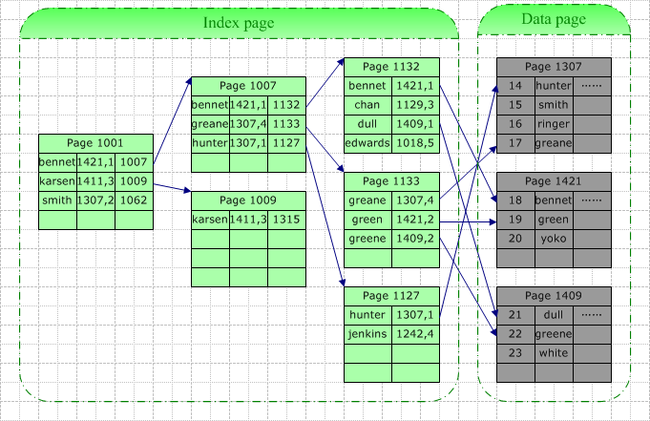
非聚集索引提供了不同的实现方案,这里索引就更像是个索引了,索引本身单独构成了B-tree,只是在每个节点的数据中记录了数据行的页地址和偏移量,这无疑使得更新数据的效率提高了,同样的数据本身也不在拥有和索引一样的顺序。最明显的特征就是,每次insert into一行,总是直接加到表的最后面的。具体实现看下面的图:
其他需要注意的地方:
tip1: 聚集索引建立在主键ID上?
虽说ID并不会频繁更新,并且单调增长的物理排序也很合理。问题在于一张表只能有一个聚集索引,因为物理顺序只能是唯一的,这意味你不能在其他字段上使用聚集索引,而应用中你会去select ID值么?尤其是自增的ID值?恐怕不大可能吧,在用户名,日期这些字段上建立聚集似乎更合理。
tip2: 复合聚集索引一定可以提高速度?
如果仅用聚集索引的起始列作为查询条件和同时用到复合聚集索引的全部列的查询速度是几乎一样的,甚至比用上全部的复合索引列还要略快(在查询结果集数目一样的情况下);而如果仅用复合聚集索引的非起始列作为查询条件的话,这个索引是不起任何作用的。