- 蓝桥杯 Java B 组之设计 LRU 缓存
计算机小白一个
java蓝桥杯算法
Day7:综合练习-设计LRU缓存一、什么是LRU(LeastRecentlyUsed)缓存?LRU(LeastRecentlyUsed)缓存是一种基于最近最少使用策略的缓存机制,用于管理固定大小的缓存,当缓存满时,会淘汰最久未被使用的元素。LRU设计核心缓存的最大容量capacity支持get(key)操作(O(1)时间复杂度)支持put(key,value)操作(O(1)时间复杂度)当缓存满时
- 使用Python获取在线股票交易网站的实时交易数据
嵌入式开发项目
2025年爬虫精通专栏python开发语言爬虫
目录步骤1:选择股票交易网站步骤2:使用requests库发送HTTP请求步骤3:解析HTML内容步骤4:提取实时交易数据步骤5:存储和使用数据在金融市场中,实时交易数据对于投资者来说具有重要的价值。实时的股票价格、交易量和其他市场指标可以帮助投资者做出更准确的决策,同时也是进行金融分析和建模的重要数据源。在本篇博客中,我们将学习如何使用Python获取在线股票交易网站的实时交易数据。在开始之前,
- Python 基础-循环
赔罪
Python系统学习pythonwindows服务器
目录简介breakcontinue小结简介要计算1+2+3,我们可以直接写表达式:>>>1+2+36要计算1+2+3+...+10,勉强也能写出来。但是,要计算1+2+3+...+10000,直接写表达式就不可能了。为了让计算机能计算成千上万次的重复运算,我们就需要循环语句。Python的循环有两种,一种是for...in循环,依次把list或tuple中的每个元素迭代出来,看例子:names=[
- vue3+vite 自动引入export default的包
大橙子-
vue.js前端
importautoImportfrom'unplugin-auto-import/vite';exportdefaultdefineConfig({plugins:[vue(),vueJsx(),autoImport({imports:['vue','vue-router','pinia',{//相当于importuseRouterStackStorefrom'@/store/modules/r
- vue制作导航栏html,Vue实现导航栏菜单
DataQueen
vue制作导航栏html
本文实例为大家分享了Vue实现导航栏菜单的具体代码,供大家参考,具体内容如下这里是刚学习vue的时候,没有用vue的任何UI组件库写的导航栏菜单。menu.html导航栏左项目名称您好,用户!v-bind:class="{checked:index==nowIndex}"v-on:click="setTab('menu',index,menus)">{{menu.text}}菜单一的内容菜单二的内
- vue3 项目如何接入 AI 大模型
代码搬运媛
人工智能
以下是在Vue3项目中接入AI大模型的一般步骤:准备工作确定要接入的AI模型,如OpenAI的gpt-3.5-turbo、科大讯飞的星火大模型等。选择AI模型及获取API密钥:注册对应AI平台的账号,进入账户设置页面找到“ViewAPIKeys”或类似选项,创建属于自己的API密钥,并妥善保存。创建Vue项目并安装依赖打开命令行,使用vuecreate项目名命令创建一个新的Vue项目,按照提示完成
- vue-router 中滚动行为设置的妙用
代码搬运媛
vue.jsjavascript前端
在vue-router里,滚动行为设置能够对路由切换时的页面滚动位置进行控制,这在单页面应用(SPA)里十分有用,能够为用户带来更流畅、更符合预期的浏览体验。下面为你详细介绍滚动行为设置的作用和使用方法。作用恢复滚动位置当用户在某个页面滚动到特定位置后,再导航到其他页面,之后又返回到该页面时,滚动行为设置可以让页面恢复到之前的滚动位置。这在浏览长页面或者列表页时非常实用,用户无需重新滚动到之前查看
- Python 队列的使用:掌握先进先出的数据结构
车载testing
python
Python队列的使用:掌握先进先出的数据结构队列是一种先进先出(FIFO)的数据结构,它在多种编程场景中都非常有用,比如任务调度、事件处理等。在Python中,我们可以通过标准库中的queue模块来实现队列。本文将详细介绍如何使用Python的queue模块来创建和操作队列。导入Queue模块使用queue模块之前,我们需要先导入它:fromqueueimportQueue创建队列创建一个队列实
- 前端框架虚拟DOM的产生
大橙子-
前端框架前端javascript
直接说结论:为了找出与命令式(原生实现步骤)所执行代码的最小差异化,从而优化代码性能。命令式:可以理解为面向过程编程,需要写好每个实现步骤constdiv=document.querySelector('#app')//获取divdiv.innerText='helloworld'//设置文本内容如果需要修改文字内容为“你好”div.innerText='你好'//设置文本内容声明式:可以理解为面
- DeepSeek 助力 Vue 开发:打造丝滑的导航栏(Navbar)
宝码香车
#DeepSeekvue.js前端javascriptecmascriptDeepSeek
前言:哈喽,大家好,今天给大家分享一篇文章!并提供具体代码帮助大家深入理解,彻底掌握!创作不易,如果能帮助到大家或者给大家一些灵感和启发,欢迎收藏+关注哦目录DeepSeek助力Vue开发:打造丝滑的导航栏(Navbar)前言页面效果指令输入属性定义1.导航栏样式相关2.导航项相关3.响应式相关4.对齐方式相关事件定义1.导航项点击事件2.菜单折叠切换事件其他建议1.可访问性2.动画效果3.图标支
- java中sort排序
Nick yang '
笔记
importjava.util.*;publicclasssortArray{publicstaticvoidmain(String[]args){int[]Array=newint[]{1,5,6,8,9,7,4,3,2,0};Arrays.sort(Array);for(intvalue:Array){System.out.print(value+"");}System.out.println
- iOS Blocks与Dispatch Queue的使用
a14776584
IOSBlocksDispatchQueuedispatch_asynciosiOSIOS
转载自http://liwpk.blog.163.com/blog/static/363261702012413103111749/block是什么block是一个Clevel的语法以及运行时的一个特性,和标准C中的函数(函数指针)类似。用于回调函数的地方。两个对象间的通讯。实现轻量级的“代理”。blocks和C语言函数指针的区别如何调用blocks调用block和C语言函数指针的调用一模一样如何
- Anaconda 国内常用镜像地址
那个发光的
anaconda
Anaconda镜像地址http://mirrors.aliyun.com/pypi/simple///阿里https://pypi.tuna.tsinghua.edu.cn/simple///清华http://pypi.douban.com///豆瓣http://pypi.hustunique.com///华中理工大学http://pypi.sdutlinux.org///山东理工大学http:
- Excel导入导出(注解)
静谧空间
exceljava开发语言
1、Excel适配器publicinterfaceExcelHandlerAdapter{/***格式化**@paramvalue单元格数据值*@paramargsexcel注解args参数组**@return处理后的值*/Objectformat(Objectvalue,String[]args);}2、自定义注解packagecom.zz.common.annotation;importjav
- vue3 + vite引入地址路径报错,以及无法点击跳转相应的文件
zmyalh
前端javascriptvue.js
vue3+vite引入地址路径报错,以及无法点击跳转相应的文件在项目中找到tsconfig.json,或者jsconfig.json文件,使用一下代码替换即可。如果两个文件都不存在,如果项目使用了ts,就创建tsconfig.json文件,复制下方代码。如果不是使用的ts,就创建jsconfig.json文件,复制下方代码。配置完成后关掉软件重启!!!{"compilerOptions":{"ba
- vue播放m3u8视频
zmyalh
html视频video前端
这里封装成组件先安装插件npmivue-video-player-S//版本"^5.0.2"npmivideojs-flash-S//播放rtmpnpmivideojs-contrib-hls-S//播放m3u8父页面://传入视频地址videoUrl页面引入importvideosfrom"../../../components/videos/videos.vue";components:{vi
- oracle序列每天重置
&loopy&
oracle数据库
在Oracle数据库中,若要实现序列每天重置,可以通过以下步骤进行操作:一、创建序列首先,需要创建一个序列。创建序列的SQL语句如下:CREATESEQUENCEsequence_nameSTARTWITH0--或其他起始值INCREMENTBY1CACHE10;--缓存大小可根据需要调整其中,sequence_name是序列的名称,STARTWITH指定序列的起始值,INCREMENTBY指定序
- vue中nextTick函数和react类似实现
向画
vue.jsreact.js前端
Vue3基本用法:import{nextTick}from'vue';//全局调用nextTick(()=>{//在下一个DOM更新循环后执行的代码});//在组件内部调用setup(){asyncfunctionhandleUpdate(){//修改数据...awaitnextTick();//在数据引发的DOM更新完成后执行的代码}}nextTick函数现在作为vue包的一个导出成员,需要显式
- Request body too large. The max request body size is 30000000 bytes.
时代的狂
异常集合c#.netcore
环境:Windows,Linux发布.net6API发起接口请求报错:Requestbodytoolarge.Themaxrequestbodysizeis30000000bytes.解决方式,Startup.cs添加如下代码://接口请求限制services.Configure(options=>{options.Limits.MaxRequestBodySize=int.MaxValue;})
- 力扣-二叉树-98 验证二叉搜索树
夏末秋也凉
力扣#二叉树leetcode算法
思路第一个特性,二叉搜索树的中序遍历是有序的,第二个特性,利用两个指针判断大小关系代码classSolution{public:TreeNode*pre=NULL;boolisValidBST(TreeNode*root){if(root==NULL)returntrue;boolleft=isValidBST(root->left);if(pre!=NULL&&pre->val>=root->v
- vue面试题|[2025-1-10]
○陈
vue面试题vue.jsjavascript前端
1.vue和jquery的区别是什么?1.原理不同vue就是数据绑定;jq是先获取dom再处理2.着重点不同vue是数据驱动,jq是着重于页面3.操作不同4.未来发展不同2.vuex的响应式处理vuex是vue的状态管理工具vue中可以直接触发methods中的方法,vuex是不可以的。处理异步,当触发事件的时候,会通过dispatch来访问actions中的方法,actions中的commit会
- 如何在C#项目中获取当前页面的URL地址
weixin_43250628
后端javascript前端html
这篇文章给大家介绍如何在C#项目中获取当前页面的URL地址,内容非常详细,感兴趣的小伙伴们可以参考借鉴,希望对大家能有所帮助。1、通过C#获取当前页面的URL复制代码代码如下:stringurl=Request.Url.AbsoluteUri;//结果:http://www.baidu.com/web/index.aspxstringhost=Request.Url.Host;//结果:www.b
- k8s rook-ceph MountDevice failed for volume pvc An operation with the given Volume ID already exists
时空无限
Kuberneteskubernetesceph
https://github.com/rook/rook/issues/4896环境kubeadm搭建的k8s集群,rook-ceph部署的ceph存储,monpod所在宿主机和挂载客户端机器pod所在机器不在一个二层网络里。故障pod挂载不上pvc,describepod信息如下MountDevicefailedforvolumepvcAnoperationwiththegivenVolumeI
- C++ STL容器大全 string vector stack queue list priority_queue set map pair
luckyyunji
C++数据结构c++
数据结构(容器)string类Vectorvector向量->不定长数组#include定义vector方法一vectorv1;vector>v2;vector>>v3;方法二vectorv1(5,10);vector>v2(5,vector(5,10));vector>>v3(5,vector(5,vector(5,10)))尾插尾删尾插v.push_back(123);尾删v.pop_back
- c++中的string、vector、list、stack、set、map等常用STL容器总结
子春_贰叁
C++c++stl
文章目录string类vectorliststackqueuepriority_queue(优先级队列)deque(双端队列)setmultisetmapunordered_mapstring类string类简介:1.string类是表示字符串的字符串类2.string在底层实际是:basic_string模板类的别名,typedefbasic_stringstring3.不能操作多字节或者变长字
- electron学习笔记
weixin_46452138
electron学习javascript
electron个人学习笔记一、electron简单了解Electron是一个跨平台的、基于Web前端技术的桌面GUI应用程序开发框架。可以使用HTML、CSS来绘制界面和控制布局,使用JavaScript来控制用户行为和业务逻辑,使用Node.js来通信、处理音频视频等,几乎所有的Web前端技术和框架(jQuery、Vue、React、Angular等)都可以应用到桌面GUI开发中。二、开发前基
- STL-vector,set,string,map,queue,priority_queue,stack,pair算法笔记
cloudless_sky
STLc++stl
STL:standardtemplatelibrary标准模板库,封装了很多实用的容器。(一)vectorvector是一个容器。是个类。底层数据结构是数组。vector:向量,变长数组,即“长度根据需要而自动改变的数组”。使用前提:#includeusingnamespacestd;1、vector定义vectorname;以上是长度可以根据需要变化的一位数组,typename可以是任何基本类型
- 【开源免费】基于Vue和SpringBoot的医院后台管理系统(附论文)
杨荧
vue.jsspringboot前端开源springcloudjavascript
本文项目编号T170,文末自助获取源码\color{red}{T170,文末自助获取源码}T170,文末自助获取源码目录一、系统介绍二、数据库设计三、配套教程3.1启动教程3.2讲解视频3.3二次开发教程四、功能截图五、文案资料5.1选题背景5.2国内外研究现状六、核心代码6.1查询数据6.2新增数据6.3删除数据一、系统介绍在管理员功能模块确定下来的基础上,对管理员各个功能进行设计,确定管理员功
- Excel核心函数VLOOKUP全解析:从入门到精通
The god of big data
大Big数据Data教程excel
一、函数概述VLOOKUP是Excel中最重要且使用频率最高的查找函数之一,全称为VerticalLookup(垂直查找)。该函数主要用于在数据表的首列查找特定值,并返回该行中指定列的对应值。根据微软官方统计,超过80%的Excel用户在日常工作中都会使用到这个函数。二、函数语法详解=VLOOKUP(lookup_value,table_array,col_index_num,[range_loo
- 教程 | Ventoy全攻略:2025最新安装与使用教程,打造万能多系统启动盘
The god of big data
教程神器?三叉戟?虚拟系统系统架构
一、Ventoy简介与核心优势Ventoy是一款开源免费的多系统启动盘工具,支持Windows、Linux、macOS等操作系统及各类维护工具。其最大特点是无需反复格式化U盘,只需将ISO/WIM/IMG等镜像文件直接拷贝至U盘即可启动,且支持LegacyBIOS与UEFI双模式。相较于传统工具,Ventoy的优势包括:多系统兼容性:支持超1000种ISO镜像,涵盖主流操作系统及工具(如Windo
- 戴尔笔记本win8系统改装win7系统
sophia天雪
win7戴尔改装系统win8
戴尔win8 系统改装win7 系统详述
第一步:使用U盘制作虚拟光驱:
1)下载安装UltraISO:注册码可以在网上搜索。
2)启动UltraISO,点击“文件”—》“打开”按钮,打开已经准备好的ISO镜像文
- BeanUtils.copyProperties使用笔记
bylijinnan
java
BeanUtils.copyProperties VS PropertyUtils.copyProperties
两者最大的区别是:
BeanUtils.copyProperties会进行类型转换,而PropertyUtils.copyProperties不会。
既然进行了类型转换,那BeanUtils.copyProperties的速度比不上PropertyUtils.copyProp
- MyEclipse中文乱码问题
0624chenhong
MyEclipse
一、设置新建常见文件的默认编码格式,也就是文件保存的格式。
在不对MyEclipse进行设置的时候,默认保存文件的编码,一般跟简体中文操作系统(如windows2000,windowsXP)的编码一致,即GBK。
在简体中文系统下,ANSI 编码代表 GBK编码;在日文操作系统下,ANSI 编码代表 JIS 编码。
Window-->Preferences-->General -
- 发送邮件
不懂事的小屁孩
send email
import org.apache.commons.mail.EmailAttachment;
import org.apache.commons.mail.EmailException;
import org.apache.commons.mail.HtmlEmail;
import org.apache.commons.mail.MultiPartEmail;
- 动画合集
换个号韩国红果果
htmlcss
动画 指一种样式变为另一种样式 keyframes应当始终定义0 100 过程
1 transition 制作鼠标滑过图片时的放大效果
css
.wrap{
width: 340px;height: 340px;
position: absolute;
top: 30%;
left: 20%;
overflow: hidden;
bor
- 网络最常见的攻击方式竟然是SQL注入
蓝儿唯美
sql注入
NTT研究表明,尽管SQL注入(SQLi)型攻击记录详尽且为人熟知,但目前网络应用程序仍然是SQLi攻击的重灾区。
信息安全和风险管理公司NTTCom Security发布的《2015全球智能威胁风险报告》表明,目前黑客攻击网络应用程序方式中最流行的,要数SQLi攻击。报告对去年发生的60亿攻击 行为进行分析,指出SQLi攻击是最常见的网络应用程序攻击方式。全球网络应用程序攻击中,SQLi攻击占
- java笔记2
a-john
java
类的封装:
1,java中,对象就是一个封装体。封装是把对象的属性和服务结合成一个独立的的单位。并尽可能隐藏对象的内部细节(尤其是私有数据)
2,目的:使对象以外的部分不能随意存取对象的内部数据(如属性),从而使软件错误能够局部化,减少差错和排错的难度。
3,简单来说,“隐藏属性、方法或实现细节的过程”称为——封装。
4,封装的特性:
4.1设置
- [Andengine]Error:can't creat bitmap form path “gfx/xxx.xxx”
aijuans
学习Android遇到的错误
最开始遇到这个错误是很早以前了,以前也没注意,只当是一个不理解的bug,因为所有的texture,textureregion都没有问题,但是就是提示错误。
昨天和美工要图片,本来是要背景透明的png格式,可是她却给了我一个jpg的。说明了之后她说没法改,因为没有png这个保存选项。
我就看了一下,和她要了psd的文件,还好我有一点
- 自己写的一个繁体到简体的转换程序
asialee
java转换繁体filter简体
今天调研一个任务,基于java的filter实现繁体到简体的转换,于是写了一个demo,给各位博友奉上,欢迎批评指正。
实现的思路是重载request的调取参数的几个方法,然后做下转换。
- android意图和意图监听器技术
百合不是茶
android显示意图隐式意图意图监听器
Intent是在activity之间传递数据;Intent的传递分为显示传递和隐式传递
显式意图:调用Intent.setComponent() 或 Intent.setClassName() 或 Intent.setClass()方法明确指定了组件名的Intent为显式意图,显式意图明确指定了Intent应该传递给哪个组件。
隐式意图;不指明调用的名称,根据设
- spring3中新增的@value注解
bijian1013
javaspring@Value
在spring 3.0中,可以通过使用@value,对一些如xxx.properties文件中的文件,进行键值对的注入,例子如下:
1.首先在applicationContext.xml中加入:
<beans xmlns="http://www.springframework.
- Jboss启用CXF日志
sunjing
logjbossCXF
1. 在standalone.xml配置文件中添加system-properties:
<system-properties> <property name="org.apache.cxf.logging.enabled" value=&
- 【Hadoop三】Centos7_x86_64部署Hadoop集群之编译Hadoop源代码
bit1129
centos
编译必需的软件
Firebugs3.0.0
Maven3.2.3
Ant
JDK1.7.0_67
protobuf-2.5.0
Hadoop 2.5.2源码包
Firebugs3.0.0
http://sourceforge.jp/projects/sfnet_findbug
- struts2验证框架的使用和扩展
白糖_
框架xmlbeanstruts正则表达式
struts2能够对前台提交的表单数据进行输入有效性校验,通常有两种方式:
1、在Action类中通过validatexx方法验证,这种方式很简单,在此不再赘述;
2、通过编写xx-validation.xml文件执行表单验证,当用户提交表单请求后,struts会优先执行xml文件,如果校验不通过是不会让请求访问指定action的。
本文介绍一下struts2通过xml文件进行校验的方法并说
- 记录-感悟
braveCS
感悟
再翻翻以前写的感悟,有时会发现自己很幼稚,也会让自己找回初心。
2015-1-11 1. 能在工作之余学习感兴趣的东西已经很幸福了;
2. 要改变自己,不能这样一直在原来区域,要突破安全区舒适区,才能提高自己,往好的方面发展;
3. 多反省多思考;要会用工具,而不是变成工具的奴隶;
4. 一天内集中一个定长时间段看最新资讯和偏流式博
- 编程之美-数组中最长递增子序列
bylijinnan
编程之美
import java.util.Arrays;
import java.util.Random;
public class LongestAccendingSubSequence {
/**
* 编程之美 数组中最长递增子序列
* 书上的解法容易理解
* 另一方法书上没有提到的是,可以将数组排序(由小到大)得到新的数组,
* 然后求排序后的数组与原数
- 读书笔记5
chengxuyuancsdn
重复提交struts2的token验证
1、重复提交
2、struts2的token验证
3、用response返回xml时的注意
1、重复提交
(1)应用场景
(1-1)点击提交按钮两次。
(1-2)使用浏览器后退按钮重复之前的操作,导致重复提交表单。
(1-3)刷新页面
(1-4)使用浏览器历史记录重复提交表单。
(1-5)浏览器重复的 HTTP 请求。
(2)解决方法
(2-1)禁掉提交按钮
(2-2)
- [时空与探索]全球联合进行第二次费城实验的可能性
comsci
二次世界大战前后,由爱因斯坦参加的一次在海军舰艇上进行的物理学实验 -费城实验
至今给我们大家留下很多迷团.....
关于费城实验的详细过程,大家可以在网络上搜索一下,我这里就不详细描述了
在这里,我的意思是,现在
- easy connect 之 ORA-12154: TNS: 无法解析指定的连接标识符
daizj
oracleORA-12154
用easy connect连接出现“tns无法解析指定的连接标示符”的错误,如下:
C:\Users\Administrator>sqlplus username/
[email protected]:1521/orcl
SQL*Plus: Release 10.2.0.1.0 – Production on 星期一 5月 21 18:16:20 2012
Copyright (c) 198
- 简单排序:归并排序
dieslrae
归并排序
public void mergeSort(int[] array){
int temp = array.length/2;
if(temp == 0){
return;
}
int[] a = new int[temp];
int
- C语言中字符串的\0和空格
dcj3sjt126com
c
\0 为字符串结束符,比如说:
abcd (空格)cdefg;
存入数组时,空格作为一个字符占有一个字节的空间,我们
- 解决Composer国内速度慢的办法
dcj3sjt126com
Composer
用法:
有两种方式启用本镜像服务:
1 将以下配置信息添加到 Composer 的配置文件 config.json 中(系统全局配置)。见“例1”
2 将以下配置信息添加到你的项目的 composer.json 文件中(针对单个项目配置)。见“例2”
为了避免安装包的时候都要执行两次查询,切记要添加禁用 packagist 的设置,如下 1 2 3 4 5
- 高效可伸缩的结果缓存
shuizhaosi888
高效可伸缩的结果缓存
/**
* 要执行的算法,返回结果v
*/
public interface Computable<A, V> {
public V comput(final A arg);
}
/**
* 用于缓存数据
*/
public class Memoizer<A, V> implements Computable<A,
- 三点定位的算法
haoningabc
c算法
三点定位,
已知a,b,c三个顶点的x,y坐标
和三个点都z坐标的距离,la,lb,lc
求z点的坐标
原理就是围绕a,b,c 三个点画圆,三个圆焦点的部分就是所求
但是,由于三个点的距离可能不准,不一定会有结果,
所以是三个圆环的焦点,环的宽度开始为0,没有取到则加1
运行
gcc -lm test.c
test.c代码如下
#include "stdi
- epoll使用详解
jimmee
clinux服务端编程epoll
epoll - I/O event notification facility在linux的网络编程中,很长的时间都在使用select来做事件触发。在linux新的内核中,有了一种替换它的机制,就是epoll。相比于select,epoll最大的好处在于它不会随着监听fd数目的增长而降低效率。因为在内核中的select实现中,它是采用轮询来处理的,轮询的fd数目越多,自然耗时越多。并且,在linu
- Hibernate对Enum的映射的基本使用方法
linzx0212
enumHibernate
枚举
/**
* 性别枚举
*/
public enum Gender {
MALE(0), FEMALE(1), OTHER(2);
private Gender(int i) {
this.i = i;
}
private int i;
public int getI
- 第10章 高级事件(下)
onestopweb
事件
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- 孙子兵法
roadrunners
孙子兵法
始计第一
孙子曰:
兵者,国之大事,死生之地,存亡之道,不可不察也。
故经之以五事,校之以计,而索其情:一曰道,二曰天,三曰地,四曰将,五
曰法。道者,令民于上同意,可与之死,可与之生,而不危也;天者,阴阳、寒暑
、时制也;地者,远近、险易、广狭、死生也;将者,智、信、仁、勇、严也;法
者,曲制、官道、主用也。凡此五者,将莫不闻,知之者胜,不知之者不胜。故校
之以计,而索其情,曰
- MySQL双向复制
tomcat_oracle
mysql
本文包括:
主机配置
从机配置
建立主-从复制
建立双向复制
背景
按照以下简单的步骤:
参考一下:
在机器A配置主机(192.168.1.30)
在机器B配置从机(192.168.1.29)
我们可以使用下面的步骤来实现这一点
步骤1:机器A设置主机
在主机中打开配置文件 ,
- zoj 3822 Domination(dp)
阿尔萨斯
Mina
题目链接:zoj 3822 Domination
题目大意:给定一个N∗M的棋盘,每次任选一个位置放置一枚棋子,直到每行每列上都至少有一枚棋子,问放置棋子个数的期望。
解题思路:大白书上概率那一张有一道类似的题目,但是因为时间比较久了,还是稍微想了一下。dp[i][j][k]表示i行j列上均有至少一枚棋子,并且消耗k步的概率(k≤i∗j),因为放置在i+1~n上等价与放在i+1行上,同理
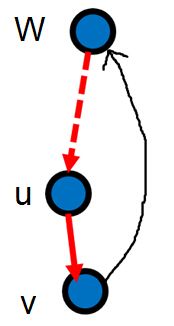 若low[v]>dfn[u],则v被封死在u的子树内,删除点u,或者删除边(u,v),都将使v与u的祖先w不连通。
若low[v]>dfn[u],则v被封死在u的子树内,删除点u,或者删除边(u,v),都将使v与u的祖先w不连通。