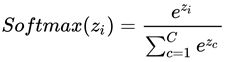MindSpore图片分类之LeNet网络池化和全连接
1. 摘要
在上一篇分享中,主要介绍了卷积操作,我们可以通过构造卷积核作用到图像中,对比输入和输出数组就可以精确的找到像素变化的位置。这便是图像物体边缘检测功能。设任意的二维数组X的i行j列的元素为X[i,j]。如果我们构造的卷积核输出Y[i,j]=1,那么说明输入中X[i,j]和X[i,j+1]数值不一样。这可能意味着物体的边缘通过这两个元素之间。
在实际图像中,我们要检测的物体不会出现在固定的位置,即使我们连续拍摄同一个物体也会出现偏移。这会导致同一个边缘对应的输出可能出现在卷积输出Y中的不同位置,从而对后面的模式识别造成困难。本片分享我们介绍池化(pooling)层,它的主要作用便是为了缓解卷积层对位置上的过度敏感性。
2. 二维最大池化层和平均池化层
和卷积计算类似,池化层每一次对输入数组的一个固定形窗口中的元素计算输出。该窗口也称池化窗口。与卷积层的运算法则不同,池化层的法则是直接计算池化窗口元素中的最大值或者平均值。所以也分别叫做最大池化和平均池化。在二维最大池化层中,池化窗口从输入数组的左上角开始,按照从左到右,从上到下的顺序,在输入数组中滑动。当池化窗口滑动到某一个位置时,窗口中的输入子数组的最大值就是输出数组中相应位置的元素。
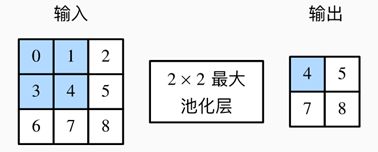
如下图1中所示,池化的窗口形状是2×2的最大池化,默认步幅都为1。阴影部分为第一个输出元素和计算所使用的输入元素。输出数组的高和宽分别为2,其中的4个元素由取最大值运算max得出:
max(0,1,3,4)=4,
max(1,2,4,5)=5,
max(3,4,6,7)=7,
max(4,5,7,8)=8.
图1:2×2最大池化层图
平均池化层的计算方法与最大池化层类似,只是将每次求池化窗口中的元素最大值改为求平均值。池化窗口形状为p×q的池化层称为p×q池化层,其中的池化运算叫作p×q池化。
在最开始我们提到的物体边缘检测的例子。现在我们将卷积层的输出作为2×2最大池化的输入。设该卷积层输入是X、池化层输出为Y。无论是X[i,j]和X[i,j+1]值不同,还是X[i,j+1]和X[i,j+2]不同,池化层输出均有Y[i,j]=1。也就是说,使用2×2最大池化层时,只要卷积层识别的模式在高和宽上移动不超过一个元素,我们依然可以将它检测出来。
3. 填充、步幅和多通道
和卷积层一样,池化层也可以在输入数组的高和宽两侧填充0元素。并可以设置窗口的移动步幅来改变输出数组形状。池化层填充和步幅与卷积层填充和步幅的工作机制一样。
池化层在处理多通道输入数组的时候,与卷积层的工作机制是不同的,卷积层中是将每个通道中的输入数组卷积运算后再相加,会导致输出通道变为1个。而池化层则是在每个出入通道中池化计算,但不将池化结果相加,可以保证输入通道数与输出通道数相同。
4. LeNet卷积网络
图2:LeNet卷积网络
如上图中所示,是LeNet卷积网络的整体流程图,整体包含8个网络层,下面我们将了解每一层的计算。
输入层:我们使用的数据集是MNIST数据集,该数据集中的样本数据都是规格为32×32的灰度图,我们以1个样本图片为例。那么我们输入的图片规格就是1×1×32×32,表示一个通道输入1个32×32的数组。
C1层:C1层中数组规格为6×1×28×28,从1×1×32×32卷积得到。首先需要6个批次的卷积数组,每一个批次中都有1个规格为5×5的卷积数组,卷积步幅默认为1。即卷积数组规格为6×1×5×5。
该卷积层共有6+1×5×5×6=156个参数,其中6个偏置参数。这一层网络**有6×1×28×28=4704个节点,每个节点和当前层5×5=25个节点相连,所以本层卷积层共有6×(1×28×28)×(1×5×5+1)=122304个全连接。
S2层:S2层的数组规格为6×1×14×14,从1×1×28×28卷积得到。使用的是2×2,步幅为1的最大池化操作,所以并不改变批次数,只是将每一个输入数组从28×28降到14×14的输出数组。
该池化层共有6×2=12个可训练参数,以及6×(1×14×14)×(2×2+1)=5880个全连接。
C3层:C3层的数组规格为16×1×10×10,从6×1×14×14卷积得到。输出通道数数改变,所以卷积数组需要16批卷积数组,每一批中有6个卷积核与输入通道对应,每一个卷积数组规格都是5×5,步幅为1。即卷积数组规格为16×6×5×5。
该卷积层共有16+1×5×5×16=2416个参数,其中16个偏置参数。这一层网络**有16×1×10×10=1600个节点,每个节点和当前层5×5=25个节点相连,所以本层卷积层共有16×(1×10×10)×(1×5×5+1)=41600个全连接。
S4层:S4层的数组规格为16×1×5×5,这一层池化与S2层池化设置相同。所以输出数组只改变每一个数组的规格,不改变数量。
该池化层共有16×2=32个可训练参数,以及16×(1×5×5)×(2×2+1)=2000个全连接。
C5层:C5层是规格为120×1的一维向量,那么需要将S4层数组转换成一维向量,输入的数组规格是1×(16×1×5×)=1×400。使用全连接层将1×400转为1×120的向量。在全连接层中,每一个节点计算处结果后,都需要再经过激活函数计算,得出的值为输出的值。
该连接层共有5×5×16=400个输入节点,参数个数为5×5×16×120+120=48120个,输出节点120个。
F6层:F6层是规格为84×1的一维向量,与C5层计算相同,也是通过全连接层计算得到。为什么要转成84个神经元向量呢,如下图中所示,是所有字符标准格式,规格为12×7.所以有84个像素点,然后使用F6层的向量与这些标准图计算相似度。
该连接层共有120个输入节点,参数个数为120×84+84=10164个,输出节点84个。
图3:字符标准图
输出层:该连接层共有84个输入节点,参数个数为84×10+10=850个,输出节点10个。
输出层使用Softmax函数做多分类,在Softmax用于多分类过程中,它将多个神经元的输出,映射到(0,1)区间中,可以看作是每一个类别的概率值,从而实现多分类。Softmax从字面上来看,可以分成Soft和max两部分。Softmax的核心是Soft,对于图片分类来说,一张图片或多或少都会包含其它类别的信息,我们更期待得到图片对于每个类别的概率值,可以简单理解为每一个类别的可信度;max就是最大值的意思,选择概率值最大的当作分类的类别。
下面给出Softmax函数的定义
图4:Softmax表达式
其中zi是第i个节点的输出值,C是输出节点的个数,即分类类别的个数。通过Softmax函数可以将多分类的输出值转换为范围在[0,1],并且总和为1的概率分布。当使用Softmax函数作为输出节点的激活函数的时候,一般使用交叉熵作为损失函数。模型有了损失函数后,就可以使用梯度下降的方法求解最优参数值。
5. 总结
本篇我们主要承接上一次的卷积内容,首先分析了池化操作的运行原理。然后使用LeNet卷积神经网络将一个32×32的灰度图的分类过程,分析了LeNet卷积神经网络网络中每一层之间卷积核信息、池化信息、参数个数、全连接个数,以及最后输出时使用的Softmax函数性质。
以上是个人的一些总结,有不足和错误之处,还请多多留言指导。