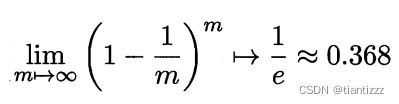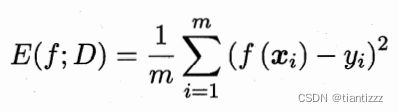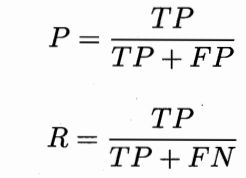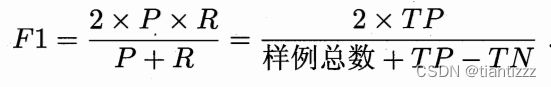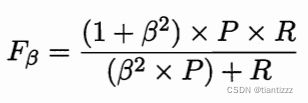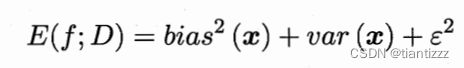机器学习（周志华）读书笔记 1

目录

1. 绪论

1.1 机器学习的基本概念

1.2 基本术语

2. 模型评估与选择

2.1 经验误差与过拟合

 2.2 评估方法

2.2.1 留出法

2.2.2 交叉验证法

2.2.3 自助法

2.2.4 调参与最终模型

2.3 性能度量

2.3.1 精度与错误率

 2.3.2 查准率与查全率

2.4比较检验

2.5 偏差与方差

---

ps.写在前面，本文是在参加datawhale组队学习，学习周志华老师的《机器学习》过程的学习笔记。文中出现的图片均引自《机器学习》，《机器学习》是初学者入门机器学习领域的很好的教材。推荐给想要入门学习机器学习领域的同路者。

1. 绪论

        在这一章中，主要分为如下几个部分：1.介绍了机器学习的基本概念，让初学者对“什么是机器学习”这一问题有了答案。2.对机器学习领域的一些相关专业术语做出解释，为后续学习做出铺垫。3.机器学习的发展历程，历史上机器学习的产生与发展。4.机器学习的主要应用现状。

1.1 机器学习的基本概念

人在日常生活中，许多时候通过看天气就可以大致判断是否会下雨，看西瓜的色泽以及听敲击西瓜的声音等判断西瓜的成熟度以及甜度。因为我们积累了大量的经验，通过经验来判断新情况的发展或是对新情况的预测。

而机器学习正是一门致力于研究如何通过计算的手段，利用经验来改善系统性能的学科。在计算机系统中，“经验”以“数据”的形式存在。因此机器学习研究的主要内容，即在计算机中，通过数据来产生模型的算法。有了数据，就可以产生出模型，模型可以给我们提供新情况的发展或预测。

1.2 基本术语

数据记录的合集称为“数据集”。每条记录称为一个“样本”或“示例”。反应对象某方面的表现或性质称为“属性”或“特征”。由属性组成的维度空间称为“属性空间”或“样本空间”。把属性作为坐标轴，空间中的每一个点都对应一个坐标向量，这样的每一个样本也称为一个“特征向量”。

从数据中学得模型的过程称为“学习”或“训练”。训练过程中使用的数据称为“训练数据”，训练数据的集合称为“训练集”。

想要进行预测，除了样本数据之外还需要另外的结果信息，这种关于样本结果的信息称为“标记”，有标记的样本则称为“样例”。所有标记的集合则称为“标记空间”。

预测任务可以分为“分类”和“回归”两类。如果预测的是离散的值，此类学习任务称为“分类”。如果预测的是连续的值，此类任务称为“回归”。对学习的模型进行预测的过程称为“测试”，被预测的样本称为“测试样本”。

根据是否有标记信息将学习任务分为“监督学习”和“无监督学习”两类，分类和回归是前者的主要代表，聚类则是后者的代表。而学习新样本的能力，则称为“泛化”。

归纳偏好：是学习算法所做出的关于什么是好的模型的假设。即在同样的训练样本下，某几种生成相同的结果。但在未知的，新的样本下，这几种模型产生的结果不同，而我们又需要选择出一种比较好的模型。归纳偏好则是用来解决这种问题。

没有免费的午餐定理：通俗讲就是，在面对不同的具体任务时，模型会有非常大的差异，大到甚至不如胡乱猜的结果。所以要具体问题具体分析，不能随便认为A模型在A1任务上表现好则在A2任务上也会表现好。

2. 模型评估与选择

在这一章中，仍然涉及了一些基本概念和术语，此外，还包括我们对模型泛化性能的评估方法、性能度量。当然，除了实验评估方法和性能度量结果之外，我们如何对结果进行比较呢？是直接的比大小吗？ 显然，对结果的比较也十分复杂，因此本章还涉及一些比较检验方法。在人们能够通过实验估计出模型的泛化能力后，又想进一步的了解“它为什么会有这样的性能呢？” 。偏差-方差分解则是解释模型泛化性能的一种重要工具。

2.1 经验误差与过拟合

• 我们把分类错误的样本数占样本总数的比例称为“错误率”。把“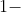错误率”称为精度。
• 把模型上实际的预测和样本的真实值之间的差异称为“误差”。
• 模型学习能力太强，导致把样本本身的特点也当作潜在规律学习，进而导致泛化能力下降，这种情况称为“过拟合”，即过于拟合训练样本，表现结果为在训练样本上表现很好，但在测试样本上可能表现不佳。同时，应注意到，过拟合是无法消除的，只能相应的“缓解”。
• 反之，学习能力太弱，没有学习到样本的潜在规律导致的在训练集和测试集上表现都不好的情况称为“欠拟合”

 2.2 评估方法

在解决实际问题的过程中，我们可能会遇到有多个模型可供选择的情况，那哪种模型的表现更好呢？这时候就需要我们使用“测试集”来测试，学习模型对新样本的预测能力，以测试集上的“测试误差”来近似泛化误差，进而判断模型的泛化能力的好坏。

这里需要注意的是，测试集作为测试使用，其中的样本尽量不要再训练集中出现，不然岂不是相当于划定范围的开卷考试了。

下面介绍几种评估方法：

2.2.1 留出法

留出法将数据集直接划分为两个互斥的集合，一部分用来做训练集，另一部分用来做测试集，在训练集上训练好的模型，拿到测试集上去看结果。这种方法要避免人为划分数据集产生的影响。要尽量将两个集合的分布做到相似。常用2/3至4/5的样本做训练集，剩余的作为测试集。

2.2.2 交叉验证法

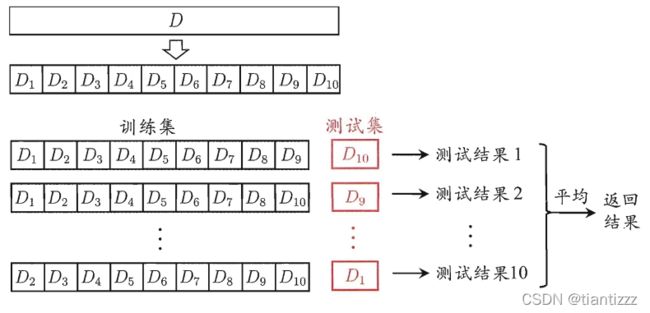
将数据集划分为K个大小相似的互斥子集，尽量保证其数据分布的一致性，然后每次用其中一个子集作为测试集，其余的都作为训练集，这样就会产生K个（训练/测试集）。再将这K次训练测试的结果取平均得到的均值作为最后结果。我们称这种方法叫“K折交叉验证”。

2.2.3 自助法

在上述两种方法（留出法、交叉验证法）中，总是会有一部分数据由于做了测试集的原因，没有训练到，有可能会和完整训练集训练的效果有差别，自助法则不会有这方面的担心，既可以减少训练样本数不同带来的影响，又可以比较高效的进行评估。

自助法的主要原理是，每次从包含m个数据的数据集D中随机采样放到D1中，重复m次后，D和D1中的数据个数相同。但显然，D中的数据有一部分没有在D1中出现，而有一部分则会重复出现。在m次采样中始终不被采到的概率为：

 也就是说，在数据集D中约有36.8%的数据是不会被采集到的，所以我们可以用D1来做训练集，D和D1的差集作为测试集。

但也要注意，自助法改变了数据的分布，会引入估计误差，所以在使用时要留意。

2.2.4 调参与最终模型

大部分模型的参数需要设定，不同的参数设定则甚至导致模型的结果有较大差异性。因此调参也是十分重要的手段。

那么如何调参呢？我们把样本分为“训练集”和“验证集”，在实际应用过程中遇到的数据称为“测试集”。“验证集”则是我们用来评估和选择模型的主要阵地。我们把在训练集上训练好的模型，通过验证集上验证，根据结果进行调参。

【注意】这里的测试集往往是我们参加比赛的模型性能评估指标。只能用一次！千万不要将模型在测试集上跑过之后再按照结果返回去修改模型来提高测试集上的分数。

2.3 性能度量

对模型的泛化能力进行评估，不仅需要有效的实验评估方法，还需要有衡量模型泛化能力的评价标准，即性能度量。在预测任务中，要评估模型f的性能，就是要把结果f（x）与真实标记y进行比较

回归任务最常用的性能度量是“均方误差”：

2.3.1 精度与错误率

• 错误率就是分类错误的样本数占样本总数的比例。
• 精度则是分类正确的样本数占样本总数的比例。

 2.3.2 查准率与查全率

有时候我们可能不想关注错误的部分，我们更想知道对于一个结果，其中正面的信息有多少被预测准确。例如一车西瓜，我们来预测是否是好瓜，我们更想知道“挑出的西瓜中有多少比例是好瓜”或是“所有好瓜中有多少比例被挑了出来”。这时候错误率就不太够用了。

查准率和查全率更适合在如下场景：在信息检索中，检索出的信息中有多少是用户感兴趣的，用户感兴趣的信息被检测出来多少。

对于分类问题，查准率和查全率分别定义为：

表 2.1 分类矩阵

真实情况 预测情况 正例 反例 正例 TP（预测为真，实际为真） FN（预测为假，实际为真） 反例 FP（预测为真，实际为假） TN（预测为假，实际为假）

查准率P和查全率R定义如下：

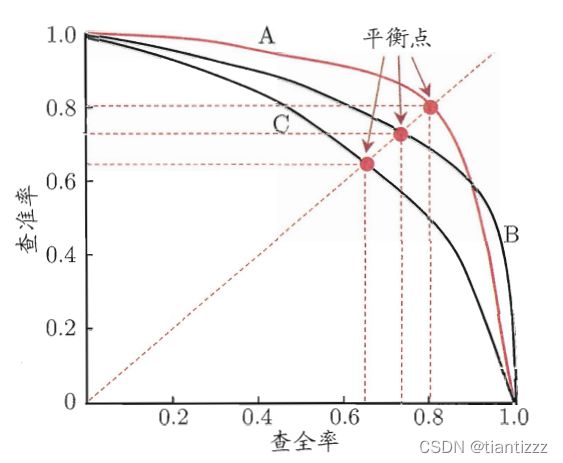
以查全率为横轴，以查准率为纵轴，绘图，则得到查准率-查全率曲线，简称“P-R曲线”。直观的显示模型在样本总体上的查全率、查准率。如果一个曲线被另一个完全“包住”，则可断言后者的性能优于前者。

“平衡点”（简称BEP）是查准率=查全率时的取值，当两条曲线相互交叉时，可以通过平衡点来判断性能。

此外，还有F1度量：

 在一些应用过程中，我们发现，对于查准率和查全率我们的重视程度是不相等的。例如在商品推荐系统中，我们会尽量推荐用户感兴趣的商品，则查准率更重要。另一方面，在追捕逃犯的筛查中，我们则更重视查全率。因此为了满足不同偏好，则出现了F1度量的一般形式：

其中度量了查全率对查准率的相对重要性，时退化为F1度量， 时查全率有更大影响，时查准率有更大影响。 

2.4比较检验

有了实验评估方法和性能度量是否就能对模型的性能进行比较了呢？实际上，机器学习中性能的比较要复杂的多，主要在如下几方面：

• 我们希望比较的是泛化性能，然而通过实验评估方法我们得到的是测试集上的性能，两者的对比结果不一定相同。
• 测试集的结果与测试集本身的选取有很大关系。不同大小，不同测试样例的结果可能不同。
• 机器学习算法本身也有一定的随机性，相同的参数同一个测试集跑多次的结果也不一定相同

因此我们要进行性能的比较不能通过直觉上的比较，可以通过统计假设检验的方法。

2.5 偏差与方差

 对学习算法除了通过实验估计其泛化性能，还想搞清楚它为什么具有这样的性能。这时候就要用到“偏差-方差分解”。

“偏差-方差分解”将分解。并得到：

可以看到，泛化误差可以分解为偏差、方差和噪声之和。

• 偏差刻画了算法本身的拟合能力，度量期望预测和真实结果的偏离程度
• 方差刻画了数据扰动所造成的影响。
• 噪声刻画了学习问题本身的难度。表明了当前任务上任何算法所能达到的期望泛化误差的下界