小白学机器学习西瓜书-第六章支持向量机(1)
小白学机器学习西瓜书-第六章支持向量机
- 6.1 间隔与支持向量
- 6.2 几何间隔
- 6.3 支持向量机
这一部分我们继续总结分类算法,支持向量机
上一部分的link:小白学机器学习西瓜书-第三章对数几率回归
6.1 间隔与支持向量
假如我们有一些样本点,他们被划分后的类别已经给出(如下图中的圆和方块是不同的样本点),那么如哦来了一个新的样本点,如图中的三角形,我们会将他划分为圆圈阵营还是方块阵营呢?
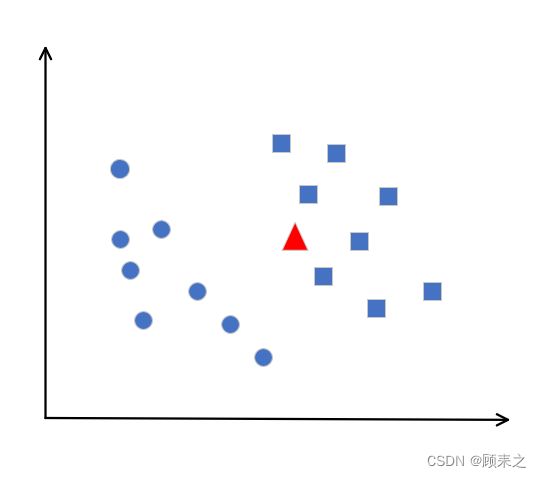
很自然的,我们会将其划分为方块那一类,因为我们在直观上已经给这些点通过一条界限划分了阵营,如下面的这些直线。只要你想要,就可以画出非常多条这样的直线。最优的直线看起来是样本正中间的那条,那是因为这条直线的抗扰动能力最强。
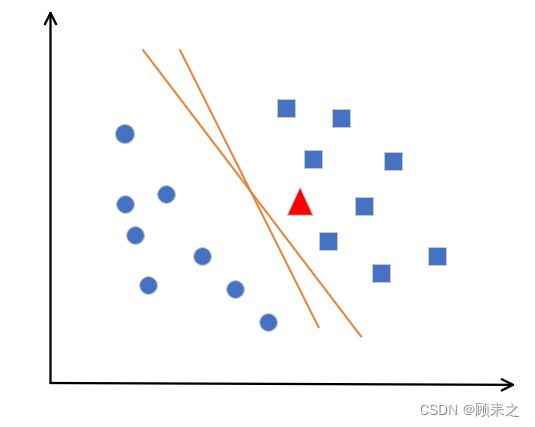
上面的例子都是两个属性样本下的分类问题,我们可以用一条直线在进行分类,如果是n个属性样本的分类问题,我们则使用超平面。
在样本空间内,这个超平面可以用线性方程来描述:
w T x + b = 0 (1) w^Tx+b=0 \tag{1} wTx+b=0(1)
其中 w = ( w 1 ; w 2 ; . . . ; w d ) w=(w_1;w_2;...;w_d) w=(w1;w2;...;wd)为法向量,即垂直于直线的一个向量,决定了超平面的方向;b为位移项,决定了超平面与原点之间的距离
w和b就可以确定确定一个超平面,我们就将由w和b确定的该超平面记为(w,b),任意点x到超平面(w,b)的距离为
r = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ (2) r=\frac{\lvert w^Tx+b \rvert}{\mid \mid w\mid\mid} \tag{2} r=∣∣w∣∣∣wTx+b∣(2)
式(2)的证明可见link:点到超平面距离
假设超平面(w,b)能将训练样本正确分类,即对于 ( x i , y i ) ∈ D (x_i,y_i) \in D (xi,yi)∈D,若 y i = + 1 y_i=+1 yi=+1,则有 w T x i + b > 0 w^Tx_i+b>0 wTxi+b>0;若 y i = − 1 y_i=-1 yi=−1,则有 w T x i + b < 0 w^Tx_i+b<0 wTxi+b<0,即
{ w T x i + b > 0 y i = + 1 w T x i + b < 0 y i = − 1 (3) \begin{cases} w^Tx_i+b> 0 & y_i=+1\\ w^Tx_i+b< 0 &y_i=-1 \tag{3} \end{cases} {wTxi+b>0wTxi+b<0yi=+1yi=−1(3)
而由于超平面 w T x + b = 0 w^Tx+b=0 wTx+b=0中的w和b可以任意进行伸缩变化(即同乘一个相同的系数)保持性质不变,我们可以将b进行拆分,将式(3)改写为
{ w T x i + b ≥ 1 y i = + 1 w T x i + b ≤ − 1 y i = − 1 (4) \begin{cases} w^Tx_i+b\geq 1 & y_i=+1\\ w^Tx_i+b\leq -1 &y_i=-1 \tag{4} \end{cases} {wTxi+b≥1wTxi+b≤−1yi=+1yi=−1(4)
而使得式(4)中的等号成立的点即为支持向量
6.2 几何间隔
接下来我们进行推导之前先插入一个叫做几何间隔的概念
对于给定的含有m个样本的集合X和超平面 w T x + b = 0 w^Tx+b=0 wTx+b=0,定义数据集中的任意一个样本点 ( x i , y i ) , y i ∈ { − 1 , 1 } (x_i,y_i),y_i \in \{-1,1\} (xi,yi),yi∈{−1,1}到超平面的几何间隔为
γ i = y i ( w T x i + b ) ∣ ∣ w ∣ ∣ (5) \gamma_i =\frac{y_i(w^Tx_i+b)}{\mid \mid w\mid\mid} \tag{5} γi=∣∣w∣∣yi(wTxi+b)(5)
从式(5)可以看出,当正确分类时,有两种情况, y i = 1 , w T x i + b > 0 y_i=1,w^Tx_i+b>0 yi=1,wTxi+b>0或者 y i = − 1 , w T x i + b < 0 y_i=-1,w^Tx_i+b<0 yi=−1,wTxi+b<0,此时 y i ( w T x i + b ) y_i(w^Tx_i+b) yi(wTxi+b) 总为正,而当错误分类时, y i ( w T x i + b ) y_i(w^Tx_i+b) yi(wTxi+b) 总为负
同时,数据集X关于超平面的几何间隔为
γ = min i = 1 , 2 , . . . , m γ i (6) \gamma= \min_{i=1,2,...,m}\gamma_i \tag{6} γ=i=1,2,...,mminγi(6)
总的来说,样本点的几何间隔的概念就是指该点到超平面的距离,但其符号如果为正代表着正确分类,其符号为负,则代表错误分类。而总的数据集到几何间隔这是所有样本点中几何间隔最小的,可想而知,如果样本点有分类错误的,那么该数据集对于该超平面的几何间隔必为负。
那么我们需要寻找的超平面是怎样的一个超平面呢?
6.3 支持向量机
对于线性可分数据集X,我们希望的超平面其实是几何间隔最大的那个超平面。
因为:
- 当没有正确分类时,数据集到超平面的几何间隔的那个为错分的点的距离的负数,此时 γ < 0 \gamma <0 γ<0
- 当正确分类时, γ ≥ 0 \gamma \geq 0 γ≥0,且数据集到超平面的几何间隔为所有样本点中到超平面距离最小的那个,所有超平面几何间隔最大的那个就是抗扰动最好的那个超平面。
得到了我们想要的超平面之后,我们将其套上sign函数实现分类(和对数几率函数一致)
y = s i g n ( w T x + b ) = { 1 w T x + b > 0 − 1 w T x + b < 0 (7) y=sign(w^Tx+b)= \begin{cases} 1 & w^Tx+b>0\\ -1 & w^Tx+b<0 \tag{7} \end{cases} y=sign(wTx+b)={1−1wTx+b>0wTx+b<0(7)
我们将要求的超平面用数学式子进行表达
max w , b y m i n ( w T x m i n + b ) ∣ ∣ w ∣ ∣ (8) \max_{w,b}\frac{y_{min}(w^Tx_{min}+b)}{\mid\mid w\mid\mid} \tag{8} w,bmax∣∣w∣∣ymin(wTxmin+b)(8)
s.t. y i ( w T x i + b ) ≥ y m i n ( w T x m i n + b ) y_i(w^Tx_i+b)\geq y_{min}(w^Tx_{min}+b) yi(wTxi+b)≥ymin(wTxmin+b)