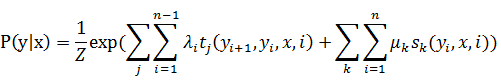机器学习笔记（七）：概率图模型

机器学习最重要的任务，是根据一些已观察到的证据（例如训练样本）来对感兴趣的未知变量（例如类别标记）进行估计和推测。概率模型提供了一种描述框架，将学习任务归结为计算变量的概率分布。概率图模型（probabilistic graphical model,简称PGM）是一类用图来表达变量相关关系的概率模型，它以图为表示工具，最常见的是用一个结点表示一个或一组随机变量，结点之间的边表示变量间的概率相关关系，即“变量关系图”。

根据边的性质不同，概率图模型可大致分为两类：第一类是使用有向无环图表示变量间的依赖关系，称为有向图模型或贝叶斯网；第二类是使用无向图表示变量间的相关关系，称为无向图模型或马尔科夫网（Markov network）.

关于贝叶斯网在上一篇文章中已有介绍，本文主要介绍马尔科夫网。

目录

• 隐马尔科夫模型
• 马尔科夫随机场
• 条件随机场

 

 

一、隐马尔科夫模型(Hidden Markov Model,简称HMM)

隐马尔科夫模型是结构最简单的动态贝叶斯网，其基本思想来源于马尔可夫过程，可看作是一个含有隐含未知参数的马尔可夫过程。（对马尔可夫过程不了解的同学可参考百度百科中的介绍

https://baike.baidu.com/item/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E8%BF%87%E7%A8%8B/2952385）

一个对马尔科夫模型直观的描述如下图所示

上图中的变量可分为两组，一组是状态变量{y1,y2,…,yn}，yi∈У表示系统在第i时刻的状态，通常假定状态变量是隐藏的、不可被观测的，因此状态变量亦称隐变量。第二组是观测变量即可以被观测到的变量{x1,x2,…,xn}，其中xi∈Х表示第i时刻的观测值。观测变量的取值仅依赖于状态变量，即xt由yt确定；而yt仅依赖于上一个时刻的状态y（t-1），即系统下一时刻的状态仅由当前状态决定，不依赖于以往的任何状态。基于这种依赖关系，所有变量的联合概率分布为

从上图与上式可以看出，想要确定一个隐马尔科夫模型主要需要知道模型的结构和三组与模型相关的参数。这三组参数分别为

1、状态转移概率：模型在各个状态间转换的概率，通常记为矩阵

 

2、输出观测概率：模型根据当前状态获得各个观测值的概率，通常记为矩阵

其中

表示在任意时刻t，若状态为si，则观测值oj被获取的概率。

 

3、初始状态概率：模型在初始时刻各状态出现的概率，通常记为

其中

表示模型的初始状态为si的概率。

  通过制定状态空间y、观测空间x和上述三组参数，就能确定一个隐马尔科夫模型，通常用其参数λ=[A,B,π]来指代。给定隐马尔科夫模型λ，它按如下过程产生观测序列：

1. 设置t=1，并根据初始状态概率π选择初始状态y1；
2. 根据状态yt和输出观测概率B选择观测变量取值xt；
3. 根据状态yt和状态转移矩阵A转移模型状态，即确定y（t+1）；
4. 若t

 

其中分别为第t时刻的状态和观测值。

 

二、马尔科夫随机场（Markov Random Field，简称MRF）

在开始介绍马尔科夫随机场前，我们先来看一看随机场的概念。简单来说，随机场可以看作是一组对应于同一样本空间的随机变量的集合。一般来说，这些随机变量之间存在依赖关系，也只有当它们之间存在依赖关系的时候，我们才会将其单独拿出来看成一个随机场才有实际意义。

   马尔科夫随机场（Markov Random Field，简称MRF），即满足马尔可夫性的随机场，是一种无向图模型，这个无向图上的每一个节点对应一个随机变量，节点之间的边对应随机变量之间有概率依赖关系。因此，马尔科夫随机场的结构本质上反应了其先验关系，也就是哪些变量之间有依赖关系是要考虑的，哪些是可以忽略的。因此，马尔科夫随机场中还定义了一组势函数，用于定义概率分布函数。

下图所示是一个简单的马尔科夫随机场的模型

对于上图中结点的一个子集，若其中任意两结点间都有边链接，则称该结点子集为一个“团”。若在一个团中加入任何一个结点都不能再形成团，则称该团为“极大团”。例如上图中{x1，x2}为一个团，{x2，x5，x6}为一个极大团。

    在马尔科夫随机场中，多个变量之间的联合概率分布能基于团分解为多个因子的乘积，每个因子仅与一个团相关。具体来说，对于n个变量x={x1，x2，….，xn}，所有团构成的集合为C，与团Q∈C对应的变量记为，则联合概率P（x）定义为

其中为与团Q对应的势函数，用于对团Q中的变量关系进行建模，Z为规范化因子，以确保P（x）是被正确定义的概率。在实际应用中，精确计算Z通常很困难，但许多任务往往并不需获得Z的精确值。

  为了在马尔可夫随机场中得到“条件独立性”，我们可以借助“分离”的策略。对马尔可夫随机场，有

• 全局马尔可夫性：给定两个变量子集的分离集，则这两个变量子集条件独立。
• 局部马尔可夫性：给定某变量的邻接变量，则该变量条件独立于其他变量。
• 成对马尔可夫性：给定所有其他变量，两个非邻接变量条件独立。

 

三、条件随机场（Conditional Random Field,简称CRF）

  条件随机场（Conditional Random Field,简称CRF）是一种判别式无向图模型。因为其强大的表达能力和出色的性能，得到了广泛的应用。条件随机场试图对多个变量在给定观测值后的条件概率进行建模，具体来说，若令x={x1,x2,…,xn}为观测序列，y={y1,y2,…,yn}为与之相应的标记序列，则条件随机场的目标是构建条件概率模型P（y|x）。

从最通用的角度来看，条件随机场本质上是给定了观察值集合的马尔可夫随机场。如果给定的马尔可夫随机场中每个随机变量下面还有观察值，我们要确定的是给定观察集合下，这个马尔可夫随机场的分布，就是条件分布，则这个马尔科夫随机场就是条件随机场。条件随机场的条件分布形式完全类似于马尔可夫随机场的分布形式，只不过多了一个观察集x。

一个典型的链式条件随机场如下图右边所示

在条件随机场中，条件概率被定义为：

其中

1. tj是定义在边上的特征函数，称为转移特征，依赖于当前和前一位置。
2. sk是定义在标记变量及结点上的特征函数，称为状态特征，依赖于当前位置。
3. λi、μk是tj、sk对应的权值。
4. 特征函数tj、sk取值为1或0，当满足特征条件时取值为1，否则为0.

 

参考文献

1. 周志华，《机器学习》
2. Daisy_HJL，《Markov随机场（MRF）和条件随机场（CRF）》，

https://blog.csdn.net/qq_28618765/article/details/78219086