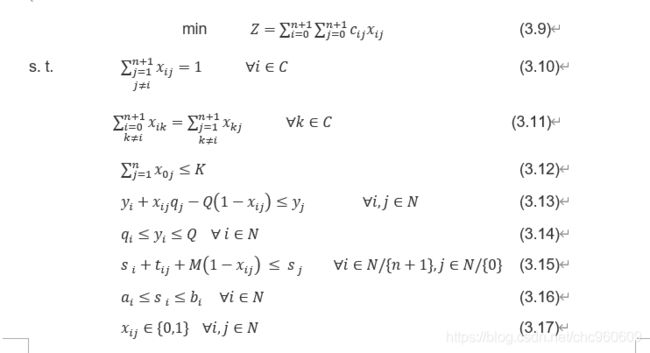旅行商问题(TSP)、车辆路径问题(VRP,MDVRP,VRPTW)模型介绍

----------------------------------------------------------------------

记20221008：私信我要模型的小伙伴很多，以加我企鹅哦（四四九零七二一二四），看到会发的

-----------------------------------------------------------------------

即将面临毕业之际，把研究生期间的研究工作的基础好好整理了一下，方便以后能快速地捡起来。写了一部分，剩下的之后继续更新。

1.旅行商问题

旅行商问题 (Traveling Salesman Problem，TSP)，又叫货郎担问题，它是图论中一个经典的组合优化问题。经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市一次并且仅一次之后，回到出发城市。问他应如何选择在城市之间的行程路线，以使他走过的总路程最短。

从图论的角度来看，该问题其实就是在一个赋权的无向图中，去找一个哈密尔顿回路，并且使得该回路的总权值最小。

容易看出，旅行商问题的可行解是N个顶点的全排列(把[1,2,3,4，...,N]打乱顺序随机排列)，其可行解的个数有(N-1)!个，也就是路线有(N-1)!个。

这里给出建模方法(参考2014 基于ＬＩＮＧＯ的旅行商问题的建模方法)：

模型1：

记为赋权图G=(V,E)，V为顶点集 ，E为边集，各顶点间的距离dij已知，N为城市数量。

模型变量：

  表示从i访问到j的弧是否被选择

                                    min                (1.1)

s. t.                                       (1.2)

                                             (1.3)

                                                  (1.4)

                                               (1.5)

Note：⊇是包含符号,前后两个集合可以相等，真包含符号就是⊂, 约束1.4即将ｎ个城市任意分成非空的两组S和 后，可行的旅行线路中应至少存在一个以S中某市ｉ为起点、  中某城市ｊ为终点的的行程.

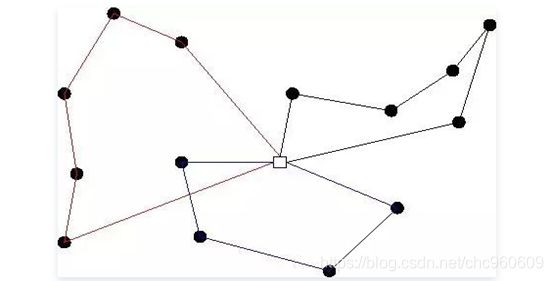
(1.1)表示最小化路径成本； (1.2) 表示每个城市点必须要出一次；(1.3) 表示每个城市点必须进一次；(1.4)表示消除子回路的约束，S是V集合除空集外的真子集，对于任意真子集要满足该约束就不会产生子回路；

上图为如果不添加子回路消除约束可能出现的情况，消除子回路的表示还有两种。

模型2：

（1.1）~（1.3）

            (2.6)

意思是对于任意数量1到V-1的点不构成回路

模型3(MTZ约束消除子环路)：

（1.1）~（1.3）

    (2.7)

                                                                    (2.8)

该约束要把起点除外， 为辅助变量没有实际意义，这种形式在模型求解时效率最高。

2.车辆路径问题（VRP）

车辆路径问题（VRP）最早是由 Dantzig 和 Ramser 于1959年首次提出，它是指一定数量的客户，各自有不同数量的货物需求，配送中心向客户提供货物，由一个车队负责分送货物，组织适当的行车路线，目标是使得客户的需求得到满足，并能在一定的约束下，达到诸如路程最短、成本最小、耗费时间最少等目的。

2.1 带有容量约束的车辆路径问题(CVRP)

该模型很难拓展到VRP的其他场景,并且不知道具体车辆的执行路径，因此对其模型继续改进。

2.2 带有多车场的车辆路径问题(MDVRP)

参考(2005 lim，多车场车辆路径问题的遗传算法_邹彤, 1996 renaud)

定义：

由于车辆是同质的，这里的建模在变量中没有加入车辆的维度。

2.3 带时间窗的车辆路径问题(VRPTW)

由于VRP问题的持续发展，考虑需求点对于车辆到达的时间有所要求之下，在车辆途程问题之中加入时窗的限制，便成为带时间窗车辆路径问题（VRP with Time Windows, VRPTW）。带时间窗车辆路径问题（VRPTW）是在VRP上加上了客户的被访问的时间窗约束。在VRPTW问题中，除了行驶成本之外, 成本函数还要包括由于早到某个客户而引起的等待时间和客户需要的服务时间。在VRPTW中，车辆除了要满足VRP问题的限制之外，还必须要满足需求点的时窗限制，而需求点的时窗限制可以分为两种，一种是硬时窗（Hard Time Window），硬时窗要求车辆必须要在时窗内到达，早到必须等待，而迟到则拒收；另一种是软时窗（Soft Time Window），不一定要在时窗内到达，但是在时窗之外到达必须要处罚，以处罚替代等待与拒收是软时窗与硬时窗最大的不同。

模型1问题定义：

The VRPTW is defined by a fleet of vehicles K={1,…,k} , a set of customers C={1,…,n} , and a directed graph G, Typically the fleet is considered to be homogeneous, that is, all vehicles are identical. The graph consists of |C| + 2 vertices, where the customers are denoted 1, 2,...,n and the depot is represented by the vertices 0 ("the starting depot") and n + 1 ("the returning depot"). The set of all vertices, that is, 0,1,... , n+1 is denoted N. The set of arcs, A, represents direct connections between the depot and the customers and among the customers. There are no arcs ending at vertex 0 or originating from vertex n + 1. With each arc (i,j), where i≠j , we associate a cost cij  and a time tij  , which may include service time at customer i.

Each vehicle has a capacity Q and each customer i a demand qi . Each customer i has a time window [ai,bi]  and a vehicle must arrive at the customer before bi . If it arrives before the time window opens, it has to wait until ai  to service the customer. The time windows for both depots are assumed to be identical to  [a0,b0]  which represents the scheduling horizon. The vehicles may not leave the depot before a0  and must return at the latest at time bn+1 .

It is assumed that Q, ai , bi , qi , cij  are non-negative integers and tij are positive integers. Note that this assumption is necessary to develop an algorithm for the shortest path with resource constraints used in the column generation approach presented later. Furthermore it is assumed that the triangle inequality is satisfied for both cij  and tij .

The decision variable s ik is defined for each vertex i and each vehicle k and denotes the time vehicle k starts to service customer i. In case vehicle k does not service customer i, s ik has no meaning and consequently it's value is considered irrelevant. We assume a0 = 0 and therefore s 0k  = 0, for all k. 

模型2(参考2017 A generalized formulation for vehicle routing problems)：

该模型为2维决策变量

2.4 VRP with Backhauls

The Vehicle Routing Problem with Backhauls (VRPB) is a VRP in which customers can demand or return some commodities. So in VRPPD it’s needed to take into account that the goods that customers return to the deliver vehicle must fit into it. The critical assumption in that all deliveries must be made on each route before any pickups can be made. This arises from the fact that the vehicles are rear-loaded, and rearrangement of the loads on the tracks at the delivery points is not deemed economical or feasible. The quantities to be delivered and picked-up are fixed and known in advance. VRPB is similar to VRPPD with the restriction that in the case of VRPB all deliveries for each route must be completed before any pickups are made.

在VRPB问题中，车辆从起点出发访问一系列客户进行送货，然后接着访问一系列客户装载货物，之后回到起点。该问题的一个关键假设是车辆必须完成送货过程然后再访问顾客进行装货。