八数码问题【人工智能实验】

一、实验题目

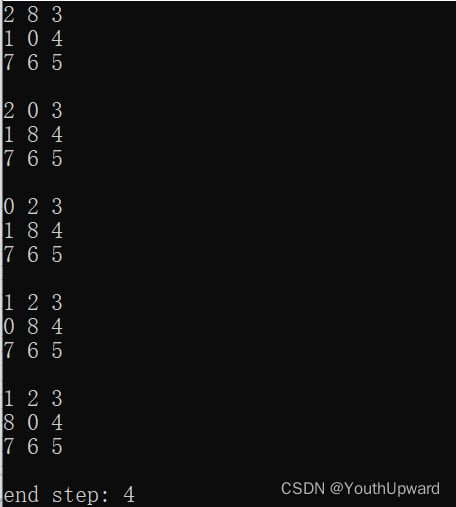
       八数码问题，也称九宫格问题，是经典的状态空间搜索问题。

二、实验分析

       因为在生成状态时，可能重复，所以该问题应当用图模型解决，即搜索建立在图上。本实验采用两种实验方法：盲目搜索算法(队列 + BFS)、启发式算法(优先队列 + BFS + 评价函数)即A*算法。
       该问题的规模为 9 ! = 362880，即有362880种可能的状态。采用盲目搜索法有的求解过程耗费时间、空间都很多，启发式算法效果比盲目搜索算法效率更高更优。

三、实验内容

1、解决方案一：盲目搜索算法

【思路】
       采用BFS搜索，一边搜索结点一边生成新的子结点。将新生成的结点放入队列queue中，将访问过的结点放入集合set中。当某结点与目标状态相同时，那么最短路径长度就是该结点的长度。而最短路径可以通过存储父节点信息已经当前的操作算子得出。
       有两个关键点：如何计算bfs中结点的层数（进而得出最短路径长度），如何记录最短路径。

2、解决方案二：启发式搜索算法

【思路】
       启发式算法是在盲目搜索算法的改进，通过评价函数f(n) = g(n) + h(n)为每个状态打分，通过放入优先队列priority_queue中，即得分低的状态结点优先访问。其他地方处理相同。其中g(n)是指到达这一状态的代价(即层数)，h(n)是指棋盘上与目标状态不同的棋子数目。
       但是有一个难点是如何证明或理解A算法的可行性。只要满足A条件，就能保证得到最优解。【A算法不能保证】

四、实验环境

Win10，vs 2019，编程语言：C++

五、实验总结

【盲目搜索算法】

1、在处理状态结点数据结构时，本来只打算简简单单地用一个二维数组来表示棋盘状态，但是在二维数组嵌套队列时，出现了问题，结构体或者类都可以替代二维数组，最终选择了类。
2、集合set嵌套结构体或者类需要重载运算符 < ，因为集合内部是需要排序，正是排序才保证set的去重功能。重载这部分比较生疏，应该多加练习。
3、在代码中，需要多次用到二维数组的比较和拷贝，本来想直接调用cstring 库中的memcpy( )和memcpy( )函数来简化代码。
4、通过代码实现，真正理解了BFS是通过队列queue实现的，而DFS是通过栈stack实现的。之前用DFS来实现回溯树，并没有通过栈来实现，而是类似于先序遍历。不过有一点可以肯定的是都不需要先全部生成树或者图，而是边生成边搜索。

【启发式搜索算法】

       A*算法也有很多改进办法和其他应用。

六、完整代码

【运行截图】

1、盲目式搜索算法

#define _CRT_SECURE_NO_WARNINGS
#include 
using namespace std;
#include 
#include 
const int N = 20;

//要将其看作图，边生成边搜索，一旦达到最终状态，那么就是结果
//现在有两个关键点：如何计算bfs的层数；如何记录路径
//结点 每个结点都是一个状态
class State
{
//由于无需涉及权限问题，故将所有成员都设为public
public:

	int Board[3][3];		//记录每个状态各个位置上的数
	int x;					//x,y标记空格的位置
	int y;
	int step;				//存储该状态的层数
	int op[N][2];			//操作数组

	//用二维数组设置棋盘上的数
	void setBoard(int board[3][3])
	{
		for (int i = 0; i < 3; i++)
		{
			for (int j = 0; j < 3; j++)
			{
				Board[i][j] = board[i][j];
			}
		}
	}

	//set函数，设置Op数组,复制父结点的Op数组，再加上自己这一步的操作
	//(i,j)表示新增的一对操作数，n表示第几层
	void setOp(int i, int j,int ParentOp[][2],int n)
	{
		for (int i = 0; i < n; i++)
		{
			op[i][0] = ParentOp[i][0];
			op[i][1] = ParentOp[i][1];
		}
		op[n][0] = i;
		op[n][1] = j;
	}

	//打印函数
	void print_board()
	{
		for (int i = 0; i < 3; i++)
		{
			for (int j = 0; j < 3; j++)
			{
				printf("%d ", Board[i][j]);
			}
			printf("\n");
		}
		printf("\n");
	}

	//因为set是要排序的，那么就要重载运算符
	bool operator < (const State b) const {
		if (memcmp(Board, b.Board, sizeof(Board)) == -1)
			return true;
		else
			return false;
	}
};

State start;	//初始状态，全局变量
State over;		//最终状态，全局变量

//四个方向向量：上下左右
int dx[4] = { -1,1,0, 0 };
int dy[4] = { 0,0,-1,1 };

queue<State> Q;	//用队列存储遍历顺序
set<State> visited;	//用集合标记访问过的结点
int stmp[3][3];

//比较两个棋盘是否相同
bool cmp(int board1[3][3], int board2[3][3]);

//State表示当前结点  (x,y)表示空格的位置
void bfs(State s)
{
	//将该结点设置为已访问过
	visited.insert(s);
	Q.pop();		//出队

	//递归调用 向四个方向生成子结点
	for (int i = 0; i < 4; i++)
	{
		int nx = s.x + dx[i];
		int ny = s.y + dy[i];

		//如果结点合法且未被访问过
		if (nx >= 0 && nx <= 2 && ny >= 0 && ny <= 2)
		{
			State tmp;
			tmp.setBoard(s.Board);		//将当前结点赋给tmp

			//生成新的结点
			swap(tmp.Board[s.x][s.y], tmp.Board[nx][ny]);
			tmp.x = nx;					//将空格信息也传递下去
			tmp.y = ny;

			tmp.step = s.step + 1;		//层数加1
			tmp.setOp(dx[i],dy[i],s.op,tmp.step);

			if (visited.count(tmp) == 0)
			{
				//将新结点加入队列中
				Q.push(tmp);

//				tmp.print_board();			//打印出来看看

				//到达最终状态
				if (cmp(tmp.Board, over.Board) == true)
				{

					//打印操作数组
				//	for (int j = 0; j < tmp.step; j++)
				//		printf("%d %d\n",tmp.op[j][0],tmp.op[j][1]);
					
					int tx = start.x;
					int ty = start.y;

					start.print_board();

					//通过操作数组逆推
					for (int j = 1; j < tmp.step; j++)
					{
						swap(stmp[tx][ty],stmp[tx + tmp.op[j][0]][ty + tmp.op[j][1]]);
						tx = tx + tmp.op[j][0];
						ty = ty + tmp.op[j][1];
						
						for (int ii = 0; ii < 3; ii++)
						{
							for (int jj = 0; jj < 3; jj++)
							{
								printf("%d ", stmp[ii][jj]);
							}
							printf("\n");
						}
						printf("\n");

					}

					over.print_board();
					printf("end step: %d\n", tmp.step);
					return;		//这个return的意义
				}
			}
		}
	}

	//开始访问下一层，访问的结点是队列的队首
	bfs(Q.front());

}

int main()
{
	//初始状态
	int s0[3][3] = {
		{2,8,3},
		{1,0,4},
		{7,6,5}
	};


	//最终状态
	int sd[3][3] = {
		{1,2,3},
		{8,0,4},
		{7,6,5}
	};

	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			stmp[i][j] = s0[i][j];
		}
	}

	int spacex = 0, spacey = 0;

	//查找并记录初始状态的空格位置
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			if (s0[i][j] == 0)
			{
				spacex = i;
				spacey = j;
				break;
			}
		}
	}

	//start
	start.setBoard(s0);   //将s0赋值给初始状态
	start.x = spacex;
	start.y = spacey;
	start.step = 0;

	Q.push(start);		 //将初始结点加入队列中
	over.setBoard(sd);	  //将sd赋值给最终状态

	bfs(start);

	return 0;
}

bool cmp(int board1[3][3], int board2[3][3])
{
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			if (board1[i][j] != board2[i][j])
			{
				return false;
			}
		}
	}

	return true;
}

2、启发式搜索算法

#define _CRT_SECURE_NO_WARNINGS
#include 
using namespace std;
#include 
#include 
const int N = 20;

//启发式算法
class State
{
public:

	int Board[3][3];		//记录每个状态各个位置上的数
	int x;					//x,y标记空格的位置
	int y;
	int step;				//存储该状态的层数,即g(n)
	int h;					//即使h(n)
	int op[N][2];			//操作数组


	//用二维数组设置棋盘上的数
	void setBoard(int board[3][3])
	{
		for (int i = 0; i < 3; i++)
		{
			for (int j = 0; j < 3; j++)
			{
				Board[i][j] = board[i][j];
			}
		}
	}

	//set函数，设置Op数组,复制父结点的Op数组，再加上自己这一步的操作
	//(i,j)表示新增的一对操作数，n表示第几层
	void setOp(int i, int j,int ParentOp[][2],int n)
	{
		for (int i = 0; i < n; i++)
		{
			op[i][0] = ParentOp[i][0];
			op[i][1] = ParentOp[i][1];
		}
		op[n][0] = i;
		op[n][1] = j;
	}

	//打印函数
	void print_board()
	{
		for (int i = 0; i < 3; i++)
		{
			for (int j = 0; j < 3; j++)
			{
				printf("%d ", Board[i][j]);
			}
			printf("\n");
		}
		printf("\n");
	}

	//因为set是要排序的，那么就要重载运算符
	bool operator < (const State b) const {
		if (memcmp(Board, b.Board, sizeof(Board)) == -1)
			return true;
		else
			return false;
	}
	
};

State start;	//初始状态，全局变量
State over;		//最终状态，全局变量

//四个方向向量：上下左右
int dx[4] = { -1,1,0, 0 };
int dy[4] = { 0,0,-1,1 };

int cost(State S);

struct cmp_cost
{
	bool operator() (State s1, State s2)
	{
		return cost(s1) > cost(s2);
	}
};

priority_queue<State,vector<State>,cmp_cost> Q;	//用优先队列存储遍历顺序
set<State> visited;	//用集合标记访问过的结点
int stmp[3][3];

//比较两个棋盘是否相同
bool cmp(int board1[3][3], int board2[3][3]);

//State表示当前结点  (x,y)表示空格的位置
void bfs(State s)
{
	//将该结点设置为已访问过
	visited.insert(s);
	Q.pop();		//出队

	//递归调用 向四个方向生成子结点
	for (int i = 0; i < 4; i++)
	{
		int nx = s.x + dx[i];
		int ny = s.y + dy[i];

		//如果结点合法且未被访问过
		if (nx >= 0 && nx <= 2 && ny >= 0 && ny <= 2)
		{
			State tmp;
			tmp.setBoard(s.Board);		//将当前结点赋给tmp

			//生成新的结点
			swap(tmp.Board[s.x][s.y], tmp.Board[nx][ny]);
			tmp.x = nx;					//将空格信息也传递下去
			tmp.y = ny;

			tmp.step = s.step + 1;		//层数加1
			tmp.setOp(dx[i],dy[i],s.op,tmp.step);

			if (visited.count(tmp) == 0)
			{
				//将新结点加入队列中
				Q.push(tmp);

//				tmp.print_board();			//打印出来看看

				//到达最终状态
				if (cmp(tmp.Board, over.Board) == true)
				{

					//打印操作数组
				//	for (int j = 0; j < tmp.step; j++)
				//		printf("%d %d\n",tmp.op[j][0],tmp.op[j][1]);
					
					int tx = start.x;
					int ty = start.y;

					start.print_board();

					//通过操作数组逆推
					for (int j = 1; j < tmp.step; j++)
					{
						swap(stmp[tx][ty],stmp[tx + tmp.op[j][0]][ty + tmp.op[j][1]]);
						tx = tx + tmp.op[j][0];
						ty = ty + tmp.op[j][1];
						
						for (int ii = 0; ii < 3; ii++)
						{
							for (int jj = 0; jj < 3; jj++)
							{
								printf("%d ", stmp[ii][jj]);
							}
							printf("\n");
						}
						printf("\n");

					}

					over.print_board();
					printf("end step: %d\n", tmp.step);
					return;		//这个return的意义
				}
			}
		}
	}

	//开始访问下一层，访问的结点是队列的队首
	bfs(Q.top());

}

int main()
{
	//初始状态
	int s0[3][3] = {
		{2,8,3},
		{1,0,4},
		{7,6,5}
	};


	//最终状态
	int sd[3][3] = {
		{1,2,3},
		{8,0,4},
		{7,6,5}
	};

	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			stmp[i][j] = s0[i][j];
		}
	}

	int spacex = 0, spacey = 0;

	//查找并记录初始状态的空格位置
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			if (s0[i][j] == 0)
			{
				spacex = i;
				spacey = j;
				break;
			}
		}
	}

	//start
	start.setBoard(s0);   //将s0赋值给初始状态
	start.x = spacex;
	start.y = spacey;
	start.step = 0;

	Q.push(start);		 //将初始结点加入队列中
	over.setBoard(sd);	  //将sd赋值给最终状态

	bfs(start);

	return 0;
}

bool cmp(int board1[3][3], int board2[3][3])
{
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			if (board1[i][j] != board2[i][j])
			{
				return false;
			}
		}
	}

	return true;
}

//传进来一个状态，将其与目的状态比较
int cost(State S)				//评价函数，f(n) = g(n) + h(n) 
{
	int h = 0;
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			if (S.Board[i][j] != over.Board[i][j])
				h++;
		}
	}

	//h的计算，值是与目的状态不同的棋子个数
	return S.step + S.h;
}