Python计算机视觉--全景图像拼接
目录
一、RANSAC算法
1.1RANSAC算法简介
1.2RANSAC算法基本思想和流程
1.3RANSAC求解单应性矩阵
二、图像映射与全景拼接
2.1简介
2.2计算第一张图像与第二章图像之间的关系
2.3将第二章图片叠加到第一张图片的坐标里
2.4图像映射的流程
2.5图像拼接流程
三、全景拼接
3.1代码
3.2拼接效果
一、RANSAC算法
1.1RANSAC算法简介
RANSAC算法的基本假设是样本中包含正确数据(inliers,可以被模型描述的数据),也包含异常数据(outliers,偏离正常范围很远、无法适应数学模型的数据),即数据集中含有噪声。这些异常数据可能是由于错误的测量、错误的假设、错误的计算等产生的。同时RANSAC也假设,给定一组正确的数据,存在可以计算出符合这些数据的模型参数的方法
1.2RANSAC算法基本思想和流程
RANSAC是通过反复选择数据集去估计出模型,一直迭代到估计出认为比较好的模型。具体的实现步骤可以分为以下几步:
(1)随机采样K个点,K是求解模型参数的最少点个数(对于直线拟合来说就是两个点(两点确定一条直线),对于拟合圆就是3个点)
(2)使用采样出的k个点估计模型参数,得到数据模型;
(3)将所有数据带入这个模型,计算出“内点”的数目;(累加在一定误差范围内的适合当前迭代得出的模型的数据);
(4)比较当前模型和之前推出的最好的模型的“内点“的数量,记录最大“内点”数的模型参数和“内点”数;
(5)重复1-4步,直到迭代结束或者当前模型已经足够好了(“内点数目大于一定数量”)。
1.3RANSAC求解单应性矩阵
单应性变换:是将一个平面内的点映射到另一个平面内的二维投影变换。
RANSAC 循环:
(1)随机选择四对匹配特征
(2)根据DLT计算单应矩阵 H (唯一解)
(3)对所有匹配点,计算映射误差ε= ||p i ’, H p i ||
(4)根据误差阈值,确定inliers(例如3-5像素)
(5)针对最大inliers集合,重新计算单应矩阵 H。
二、图像映射与全景拼接
2.1简介
首先是在连续图像对间使用SIFT特征寻找匹配对应点对,SIFT是具有较强稳健性的描述子,能够比其他描述子产生更少的错误点,但是该方法仍不是很完美;使用RANSAC算法估计出图像间的单应性矩阵,判定哪些点对是正确的,哪些点对是错误的,即使用一个阈值来决定哪些单应性矩阵是合理的;然后将所有的图像扭曲到一个公共的图像平面上。
通常,这里的公共平面为中心图像平面。一种方法是创建一个很大的图像,比如将图像中全部填充0,使其和中心图像平行,然后将所有的图像扭曲到上面。由于我们所有的图像是由照相机水平旋转拍摄的,因此我们可以使用一个较简单的步骤:将中心图像左边或者右边的区域填充为0,以便为扭曲的图像腾出空间。
图像拼接的几何原理:全景融合的 3D 几何解释,图像被投影到共同的拼接平面上(同一坐标系), 在拼接平面上实现全景融合。在拼接的应用中,其实可以简化理解为 2D图像的变换,叠加过程。
基础流程:
① 针对某个场景拍摄多张 / 序列图像
② 计算第二张图像与第一张图像之间的变换关系
③ 将第二张图像叠加到第一张图像的坐标系中
④ 变换后的融合 / 合成
⑤ 在多图场景中,重复上述过程
2.2计算第一张图像与第二章图像之间的关系
(1)变换类型选择
将两幅图像叠加在一起,选择需要采用模型,如位移、旋转、尺度大小、仿射和透视等。
(2)2D 图像变换原理:
图像滤波: 改变图像的像素点取值范围![]()
图像变换: 改变图像的坐标取值范围![]()
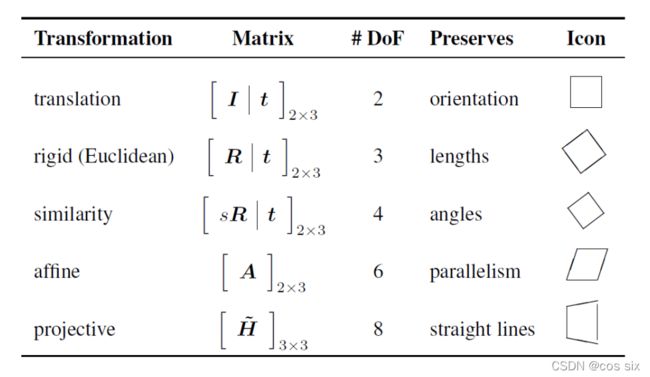
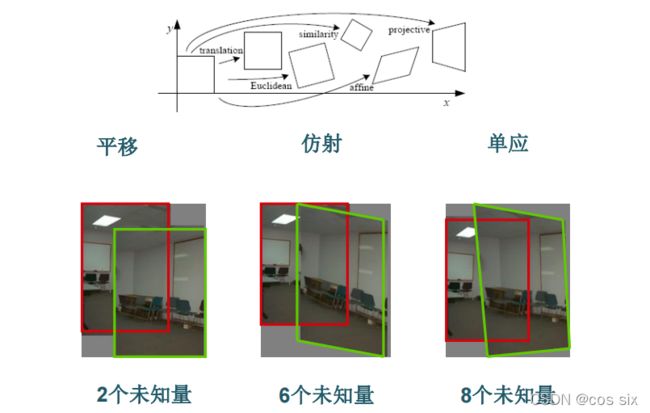
(3)2D 图像变换类型
(4)参数求解
针对不同问题,需要多少对匹配特征才能计算出模型参数。
2.3将第二章图片叠加到第一张图片的坐标里
给定变换模型 x'= h(x) ,以及输入图像f(x), 根据f(x)计算变换后的图像 g(x')= f(h(x))。前向映
射:对于 f(x) 中的每个像素 x,根据变换模型计算相应的映射坐标x' = h(x),并将x的像素值赋给
g(x')。逆向映射:对于 g(x')中的每个像素 x',根据变换模型计算相应的映射坐标 x = h -1 (x'),并
将x的像素值赋给g(x')。
2.4图像映射的流程
1)针对两张/多张图像提取特征
(2)特征匹配
(3)根据图像变换特点,选取合适的变换结构
(4)根据DLT等方法计算变换结构
(5)采用正向/逆向映射,利用插值方式实现图像映射变换
2.5图像拼接流程
(1)根据给定图像/集, 实现特征匹配
(2)通过匹配特征计算图像之间的变换结构
(3)利用图像变换结构, 实现图像映射
(4)针对叠加后的图像, 采用APAP算法对齐特征点
(5)通过图割方法, 自动选取拼接缝
(6)根据multi-band bleing策略实现融合
三、全景拼接
3.1代码
任何模型中都可以使用 RANSAC 模块,在使用 RANSAC 模块时,我们只需要在相应 Python 类中实现 fit() 和 get_error() 方法,剩下就是正确地使用 ransac.py。我们这里使用可能的对应点集来自动找到用于全景图像的单应性矩阵。
可以使用 SIFT 特征自动找到匹配对应
代码如下:
featname = ['D:/SHIJUE/SY5/jmu/p' + str(i + 1) + '.sift' for i in range(5)] # 图片路径记得修改
imname = ['D:/SHIJUE/SY5/jmu/p' + str(i + 1) + '.jpg' for i in range(5)]
# extract features and match
l = {}
d = {}
for i in range(5):
sift.process_image(imname[i], featname[i])
l[i], d[i] = sift.read_features_from_file(featname[i])
matches = {}
for i in range(4):
matches[i] = sift.match(d[i + 1], d[i])
得到效果图:
显然,并不是所有图像中的对应点对都是正确的。实际上,SIFT 是具有很强稳健性的描述子,能够比其他描述子,例如图像块相关的 Harris 角点,产生更少的错误的匹配。但是该方法仍然远非完美
可以将 RANSAC 算法应用于对应点对上:
def convert_points(j):
ndx = matches[j].nonzero()[0]
fp = homography.make_homog(l[j+1][ndx,:2].T)
ndx2 = [int(matches[j][i]) for i in ndx]
tp = homography.make_homog(l[j][ndx2,:2].T)
return fp,tp
# 估计单应性矩阵
model = homography.RansacModel()
fp,tp = convert_points(1)
H_12 = homography.H_from_ransac(fp,tp,model)[0] # im1 到 im2 的单应性矩阵
fp,tp = convert_points(0)
H_01 = homography.H_from_ransac(fp,tp,model)[0] # im0 到 im1 的单应性矩阵
tp,fp = convert_points(2) # 注意:点是反序的
H_32 = homography.H_from_ransac(fp,tp,model)[0] # im3 到 im2 的单应性矩阵
tp,fp = convert_points(3) # 注意:点是反序的
H_43 = homography.H_from_ransac(fp,tp,model)[0] # im4 到 im3 的单应性矩阵
源代码:
# -*- coding: utf-8 -*-
from pylab import *
from numpy import *
from PIL import Image
# If you have PCV installed, these imports should work
from PCV.geometry import homography, warp
from PCV.localdescriptors import sift
np.seterr(invalid='ignore')
"""
This is the panorama example from section 3.3.
"""
# set paths to data folder
featname = ['D:/SHIJUE/SY5/jmu/p' + str(i + 1) + '.sift' for i in range(5)] # 图片路径记得修改
imname = ['D:/SHIJUE/SY5/jmu/p' + str(i + 1) + '.jpg' for i in range(5)]
# extract features and match
l = {}
d = {}
for i in range(5):
sift.process_image(imname[i], featname[i])
l[i], d[i] = sift.read_features_from_file(featname[i])
matches = {}
for i in range(4):
matches[i] = sift.match(d[i + 1], d[i])
# visualize the matches (Figure 3-11 in the book)
for i in range(4):
im1 = array(Image.open(imname[i]))
im2 = array(Image.open(imname[i + 1]))
figure()
sift.plot_matches(im2, im1, l[i + 1], l[i], matches[i], show_below=True)
# function to convert the matches to hom. points
def convert_points(j):
ndx = matches[j].nonzero()[0]
fp = homography.make_homog(l[j + 1][ndx, :2].T)
ndx2 = [int(matches[j][i]) for i in ndx]
tp = homography.make_homog(l[j][ndx2, :2].T)
# switch x and y - TODO this should move elsewhere
fp = vstack([fp[1], fp[0], fp[2]])
tp = vstack([tp[1], tp[0], tp[2]])
return fp, tp
# estimate the homographies
model = homography.RansacModel()
fp, tp = convert_points(1)
H_12 = homography.H_from_ransac(fp, tp, model)[0] # im 1 to 2
fp, tp = convert_points(0)
H_01 = homography.H_from_ransac(fp, tp, model)[0] # im 0 to 1
tp, fp = convert_points(2) # NB: reverse order
H_32 = homography.H_from_ransac(fp, tp, model)[0] # im 3 to 2
tp, fp = convert_points(3) # NB: reverse order
H_43 = homography.H_from_ransac(fp, tp, model)[0] # im 4 to 3
# warp the images
delta = 1600 # for padding and translation
im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12, im1, im2, delta, delta)
im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12, H_01), im1, im_12, delta, delta)
im1 = array(Image.open(imname[3]), "f")
im_32 = warp.panorama(H_32, im1, im_02, delta, delta)
im1 = array(Image.open(imname[4]), "f")
im_42 = warp.panorama(dot(H_32, H_43), im1, im_32, delta, 2 * delta)
figure()
imshow(array(im_02, "uint8"))
axis('off')
savefig("example1.png", dpi=300)
show()
3.2拼接效果