pytorch 建立LSTM模型实现股价预测

本文参考了这篇知乎文章：https://zhuanlan.zhihu.com/p/128927771，并对其中部分代码进行修改，使其更有可读性。
原版代码和数据见此链接：https://link.zhihu.com/?target=https%3A//github.com/yhannahwang/stock_prediction

本文通过jupyter notebook转化成markdown文件，再放到这里，代码和文字可能会有部分有背景色
阅读本文之前，需要知道LSTM的原理，还有pytorch中LSTM的接口定义，否则读起来很吃力。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

导入数据，并进行处理

dates = pd.date_range('2010-10-11','2017-10-11',freq = 'B')   # 生成时间序列，频率为工作日

# 生成一个只含索引的DataFrame
df_main   = pd.DataFrame(index = dates)                           
df_main

2010-10-11
2010-10-12
2010-10-13
2010-10-14
2010-10-15
...
2017-10-05
2017-10-06
2017-10-09
2017-10-10
2017-10-11

1828 rows × 0 columns

df_aaxj   = pd.read_csv("data/ETFs/aaxj.us.txt", index_col=0)
df_aaxj

	Open	High	Low	Close	Volume	OpenInt
Date
2008-08-15	44.886	44.886	44.886	44.886	112	0
2008-08-18	44.564	44.564	43.875	43.875	28497	0
2008-08-19	43.283	43.283	43.283	43.283	112	0
2008-08-20	43.918	43.918	43.892	43.892	4468	0
2008-08-22	44.097	44.097	44.017	44.071	4006	0
...	...	...	...	...	...	...
2017-11-06	75.900	76.530	75.890	76.530	1313730	0
2017-11-07	76.490	76.580	76.090	76.185	1627277	0
2017-11-08	76.370	76.590	76.290	76.570	681128	0
2017-11-09	76.040	76.200	75.580	76.110	1261567	0
2017-11-10	76.110	76.150	75.870	76.080	619687	0

2325 rows × 6 columns

# 数据拼接
df_main   = df_main.join(df_aaxj)
df_main

	Open	High	Low	Close	Volume	OpenInt
2010-10-11	55.971	56.052	55.863	56.052	268544.0	0.0
2010-10-12	55.676	55.792	55.362	55.667	817951.0	0.0
2010-10-13	56.472	56.867	56.401	56.569	999413.0	0.0
2010-10-14	56.733	56.742	56.293	56.579	661897.0	0.0
2010-10-15	56.893	56.893	56.194	56.552	245001.0	0.0
...	...	...	...	...	...	...
2017-10-05	73.500	74.030	73.500	73.970	2134323.0	0.0
2017-10-06	73.470	73.650	73.220	73.579	2092100.0	0.0
2017-10-09	73.500	73.795	73.480	73.770	879600.0	0.0
2017-10-10	74.150	74.490	74.150	74.480	1878845.0	0.0
2017-10-11	74.290	74.645	74.210	74.610	1168511.0	0.0

1828 rows × 6 columns

# 绘制收盘价格走势图
df_main[['Close']].plot()
plt.ylabel("stock_price")
plt.title("aaxj ETFs")
plt.show()

# 筛选四个变量，作为数据的输入特征
sel_col = ['Open', 'High', 'Low', 'Close']   
df_main = df_main[sel_col]
df_main.head()

	Open	High	Low	Close
2010-10-11	55.971	56.052	55.863	56.052
2010-10-12	55.676	55.792	55.362	55.667
2010-10-13	56.472	56.867	56.401	56.569
2010-10-14	56.733	56.742	56.293	56.579
2010-10-15	56.893	56.893	56.194	56.552

# 查看是否有缺失值
np.sum(df_main.isnull())

Open     65
High     65
Low      65
Close    65
dtype: int64

# 缺失值填充
df_main = df_main.fillna(method='ffill')      # 缺失值填充，使用上一个有效值
np.sum(df_main.isnull())

Open     0
High     0
Low      0
Close    0
dtype: int64

# 数据缩放
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(-1, 1))  
for col in sel_col:                           # 这里不能进行统一进行缩放，因为fit_transform返回值是numpy类型
    df_main[col] = scaler.fit_transform(df_main[col].values.reshape(-1,1))

# 将下一日的收盘价作为本日的标签
df_main['target'] = df_main['Close'].shift(-1)   
df_main.head()

	Open	High	Low	Close	target
2010-10-11	-0.089800	-0.135104	-0.074936	-0.106322	-0.129274
2010-10-12	-0.107350	-0.150977	-0.104289	-0.129274	-0.075502
2010-10-13	-0.059996	-0.085348	-0.043415	-0.075502	-0.074905
2010-10-14	-0.044469	-0.092979	-0.049742	-0.074905	-0.076515
2010-10-15	-0.034950	-0.083761	-0.055543	-0.076515	-0.068407

df_main.dropna()                      # 使用了shift函数，在最后必然是有缺失值的，这里去掉缺失值所在行
df_main = df_main.astype(np.float32)  # 修改数据类型

建立LSTM模型

import torch.nn as nn

input_dim = 4      # 数据的特征数
hidden_dim = 32    # 隐藏层的神经元个数
num_layers = 2     # LSTM的层数
output_dim = 1     # 预测值的特征数
                   #（这是预测股票价格，所以这里特征数是1，如果预测一个单词，那么这里是one-hot向量的编码长度）
class LSTM(nn.Module):
    def __init__(self, input_dim, hidden_dim, num_layers, output_dim):
        super(LSTM, self).__init__()
        # Hidden dimensions
        self.hidden_dim = hidden_dim

        # Number of hidden layers
        self.num_layers = num_layers

        # Building your LSTM
        # batch_first=True causes input/output tensors to be of shape (batch_dim, seq_dim, feature_dim)
        self.lstm = nn.LSTM(input_dim, hidden_dim, num_layers, batch_first=True)

        # Readout layer 在LSTM后再加一个全连接层，因为是回归问题，所以不能在线性层后加激活函数
        self.fc = nn.Linear(hidden_dim, output_dim) 

    def forward(self, x):
        # Initialize hidden state with zeros   
        h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_dim).requires_grad_() 
        # 这里x.size(0)就是batch_size

        # Initialize cell state
        c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_dim).requires_grad_()

        # One time step
        # We need to detach as we are doing truncated backpropagation through time (BPTT)
        # If we don't, we'll backprop all the way to the start even after going through another batch
        out, (hn, cn) = self.lstm(x, (h0.detach(), c0.detach()))

        out = self.fc(out) 

        return out

按照模型的接口组织数据

# 创建两个列表，用来存储数据的特征和标签
data_feat, data_target = [],[]

# 设每条数据序列有20组数据
seq = 20

for index in range(len(df_main) - seq):
    # 构建特征集
    data_feat.append(df_main[['Open', 'High', 'Low', 'Close']][index: index + seq].values)
    # 构建target集
    data_target.append(df_main['target'][index:index + seq])

# 将特征集和标签集整理成numpy数组
data_feat = np.array(data_feat)
data_target = np.array(data_target)

训练集与测试集的划分

# 这里按照8:2的比例划分训练集和测试集
test_set_size = int(np.round(0.2*df_main.shape[0]))  # np.round(1)是四舍五入，
train_size = data_feat.shape[0] - (test_set_size) 
print(test_set_size)  # 输出测试集大小
print(train_size)     # 输出训练集大小

366
1442

trainX = torch.from_numpy(data_feat[:train_size].reshape(-1,seq,4)).type(torch.Tensor)   
# 这里第一个维度自动确定，我们认为其为batch_size，因为在LSTM类的定义中，设置了batch_first=True
testX  = torch.from_numpy(data_feat[train_size:].reshape(-1,seq,4)).type(torch.Tensor)
trainY = torch.from_numpy(data_target[:train_size].reshape(-1,seq,1)).type(torch.Tensor)
testY  = torch.from_numpy(data_target[train_size:].reshape(-1,seq,1)).type(torch.Tensor)

print('x_train.shape = ',trainX.shape)
print('y_train.shape = ',trainY.shape)
print('x_test.shape = ',testX.shape)
print('y_test.shape = ',testY.shape)

x_train.shape =  torch.Size([1442, 20, 4])
y_train.shape =  torch.Size([1442, 20, 1])
x_test.shape =  torch.Size([366, 20, 4])
y_test.shape =  torch.Size([366, 20, 1])

建立数据导入器（略）

# 因为数据量不大，所以这里就不再划分batch，即认为batch_size=1442，
# 这里只是演示一下数据导入器，我们并不使用

batch_size=1442
train = torch.utils.data.TensorDataset(trainX,trainY)
test = torch.utils.data.TensorDataset(testX,testY)
train_loader = torch.utils.data.DataLoader(dataset=train, 
                                           batch_size=batch_size, 
                                           shuffle=False)

test_loader = torch.utils.data.DataLoader(dataset=test, 
                                          batch_size=batch_size, 
                                          shuffle=False)

训练模型

# 实例化模型
model = LSTM(input_dim=input_dim, hidden_dim=hidden_dim, output_dim=output_dim, num_layers=num_layers)

# 定义优化器和损失函数
optimiser = torch.optim.Adam(model.parameters(), lr=0.01) # 使用Adam优化算法
loss_fn = torch.nn.MSELoss(size_average=True)             # 使用均方差作为损失函数

# 设定数据遍历次数
num_epochs = 100

# 打印模型结构
print(model)

LSTM(
  (lstm): LSTM(4, 32, num_layers=2, batch_first=True)
  (fc): Linear(in_features=32, out_features=1, bias=True)
)

# 打印模型各层的参数尺寸
for i in range(len(list(model.parameters()))):
    print(list(model.parameters())[i].size())

torch.Size([128, 4])
torch.Size([128, 32])
torch.Size([128])
torch.Size([128])
torch.Size([128, 32])
torch.Size([128, 32])
torch.Size([128])
torch.Size([128])
torch.Size([1, 32])
torch.Size([1])

# train model
hist = np.zeros(num_epochs)
for t in range(num_epochs):
    # Initialise hidden state
    # Don't do this if you want your LSTM to be stateful
    # model.hidden = model.init_hidden()
    
    # Forward pass
    y_train_pred = model(trainX)

    loss = loss_fn(y_train_pred, trainY)
    if t % 10 == 0 and t !=0:                  # 每训练十次，打印一次均方差
        print("Epoch ", t, "MSE: ", loss.item())
    hist[t] = loss.item()

    # Zero out gradient, else they will accumulate between epochs 将梯度归零
    optimiser.zero_grad()

    # Backward pass
    loss.backward()
    
    # Update parameters
    optimiser.step()

Epoch  10 MSE:  0.01842750422656536
Epoch  20 MSE:  0.008485360071063042
Epoch  30 MSE:  0.004656758159399033
Epoch  40 MSE:  0.0032537723891437054
Epoch  50 MSE:  0.002434148220345378
Epoch  60 MSE:  0.0020096886437386274
Epoch  70 MSE:  0.0018414082005620003
Epoch  80 MSE:  0.0017679394222795963
Epoch  90 MSE:  0.0017151187639683485

# 计算训练得到的模型在训练集上的均方差
y_train_pred = model(trainX)
loss_fn(y_train_pred, trainY).item()

0.0016758530400693417

测试模型

# make predictions
y_test_pred = model(testX)
loss_fn(y_test_pred, testY).item()

0.004057767800986767

# 从结果来看，有些过拟合

绘制效果图

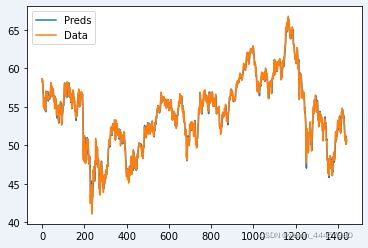
"训练集效果图"
# 无论是真实值，还是模型的输出值，它们的维度均为（batch_size, seq, 1），seq=20
# 我们的目的是用前20天的数据预测今天的股价，所以我们只需要每个数据序列中第20天的标签即可
# 因为前面用了使用DataFrame中shift方法，所以第20天的标签，实际上就是第21天的股价
pred_value = y_train_pred.detach().numpy()[:,-1,0]       
true_value = trainY.detach().numpy()[:,-1,0] 

plt.plot(pred_value, label="Preds")    # 预测值
plt.plot(true_value, label="Data")    # 真实值
plt.legend()
plt.show()

# 纵坐标还有负的，因为前面进行缩放，现在让数据还原成原来的大小
# invert predictions
pred_value = scaler.inverse_transform(pred_value.reshape(-1, 1))
true_value = scaler.inverse_transform(true_value.reshape(-1, 1))

plt.plot(pred_value, label="Preds")    # 预测值
plt.plot(true_value, label="Data")    # 真实值
plt.legend()
plt.show()

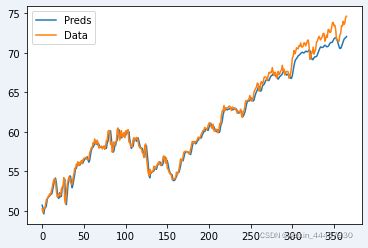
"测试集效果图"
pred_value = y_test_pred.detach().numpy()[:,-1,0]    
true_value = testY.detach().numpy()[:,-1,0]

pred_value = scaler.inverse_transform(pred_value.reshape(-1, 1))
true_value = scaler.inverse_transform(true_value.reshape(-1, 1))

plt.plot(pred_value, label="Preds")    # 预测值
plt.plot(true_value, label="Data")    # 真实值
plt.legend()
plt.show()

前面还拟合的比较好，但是到了后面的时期就不太准确了，可能与前面模型出现过拟合有关系