图论进阶版 拓扑排序+Dijkstra+ 有边数限制的最短路(Bellman - ford)+spfa(bf优化)+floyd+最小生成树
有向图的拓扑序列
有向无环图一定是拓扑序列,有向有环图一定不是拓扑序列
拓扑排序
一个有向图,如果图中有入度为 0 的点,就把这个点删掉,同时也删掉这个点所连的边。
一直进行上面出处理,如果所有点都能被删掉,则这个图可以进行拓扑排序。
模板
bool topsort()
{
int hh = 0, tt = -1;
// d[i] 存储点i的入度
for (int i = 1; i <= n; i ++ )
if (!d[i])
q[ ++ tt] = i;
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (-- d[j] == 0)
q[ ++ tt] = j;
}
}
// 如果所有点都入队了,说明存在拓扑序列;否则不存在拓扑序列。
return tt == n - 1;
}
作者:yxc
链接:https://www.acwing.com/blog/content/405/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。代码
#include
#include
#include
using namespace std;
const int N=100010;
int h[N],e[N],ne[N],idx;
int n,m;
int q[N],d[N];//q表示队列,d表示点的入度
void add(int a,int b)
{
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
bool topsort()
{
int hh=0,tt=-1;
for(int i=1;i<=n;i++)
if(!d[i])
q[++tt]=i;//将入度为零的点入队
while(hh<=tt)
{
int t=q[hh++];
//队列不空,则取出头节点
for(int i=h[t];i!=-1;i=ne[i]) //遍历头节点的每一个出边
{
int j=e[i];
d[j]--;//删除点t指向点j的边
if(d[j]==0)//如果点j的入度为零了,就将点j入队
q[++tt]=j;
}
}
return tt==n-1;
//表示如果n个点都入队了话,那么该图为拓扑图,返回true,否则返回false
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof(h));//如果程序时间溢出,就是没有加上这一句
for(int i=0;i Dijkstra算法的3个步骤
1、找到当前未标识的且离源点最近的点t
2、对t号点点进行标识
3、用t号点更新其他点的距离
Dijkstra求最短路 I(朴素版)
思路
模板
int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定
// 求1号点到n号点的最短路,如果不存在则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i ++ )
{
int t = -1; // 在还未确定最短路的点中,寻找距离最小的点
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
// 用t更新其他点的距离
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], dist[t] + g[t][j]);
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
作者:yxc
链接:https://www.acwing.com/blog/content/405/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。代码详解
#include
using namespace std;
const int N=501;
int n,m;
int g[N][N],dist[N];//g[a][b]存储从a点到b点的最短距离,dist[i]从第一个点到达i的最短距离
bool st[N];//st[i]判断i点的最短距离是否已经确定
int d(){
memset(dist,0x3f,sizeof dist);//先把所有第一个点以外的点的最短距离赋予正无穷(巨大值)
dist[1]=0;
for(int i=1;i<=n;i++){
int t=-1;
//如果没有更新过,则进行更新t, 或者发现更短的路径*,则进行更新
for(int j=1;j<=n;j++){
if(!st[j]&&(t==-1||dist[t]>dist[j])){
t=j;
}
}
st[t]=true;
for(int j=1;j<=n;j++)
dist[j]=min(dist[j],dist[t]+g[t][j]);//考虑从第一个点到j近还是先到t再到j近
}
if (dist[n]==0x3f3f3f3f) return -1;//如果起点到达不了n号节点,则返回-1
else return dist[n];
}
int main(){
cin>>n>>m;
memset(g,0x3f,sizeof(g));//memset 按字节赋值,所以memset 0x3f 就等价与赋值为0x3f3f3f3f,
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
g[a][b]=min(g[a][b],c);//如果有重边,请保留权值最小的一条边
}
int t=d();
cout< Dijkstra求最短路 II(堆优化版)
区别
n是点,m是边
判断主要是看边的数量
m和n^2是一个级别,是稠密图
m和n一个级别,是稀疏图
稠密图使用邻接矩阵存储
代码详解
#include
using namespace std;
const int N=1e6+10;
int n,m;
typedef pair PII;//<离1号点的最短距离,当前点的编号>
int h[N],e[N],ne[N],idx,w[N],dist[N];//稀疏图使用邻接表储存
bool st[N];//判断当前点的最短路是否确定
void add(int a,int b,int c){
e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}
int d(){
memset(dist,0x3f,sizeof dist);// 所有距离初始化为无穷大
dist[1]=0;// 1号节点距离为0
priority_queue, greater> heap;//建立小根堆
heap.push({0,1});//1号点入堆
while(heap.size()){
auto t=heap.top();
heap.pop();
int x=t.first;
int y=t.second;
if(st[t.second])continue;
st[t.second]=true;
for(int i=h[y];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]>dist[y]+w[i]){//dist[j] 大于从t过来的距离
dist[j]=dist[y]+w[i];
heap.push({dist[j],j});
}
}
}
if(dist[n]==0x3f3f3f3f) return -1;
else return dist[n];
}
int main(){
cin>>n>>m;
memset(h,-1,sizeof(h));
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
int t=d();
cout< 有边数限制的最短路//Bellman - ford
为什么Dijkstra不能使用在含负权的图中?
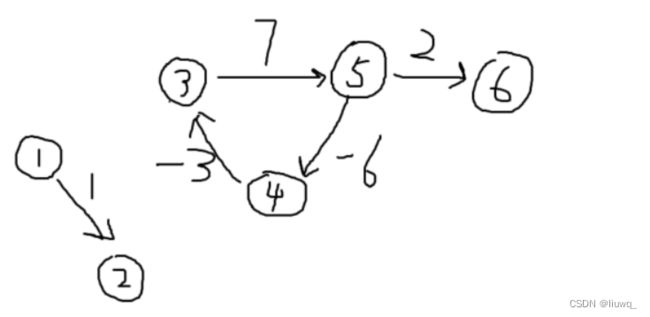
dijkstra算法在图中走出来的最短路径是1 -> 2 -> 4 -> 5,算出 1 号点到 5 号点的最短距离是2 + 2 + 1 = 5,然而还存在一条路径是1 -> 3 -> 4 -> 5,该路径的长度是5 + (-2) + 1 = 4,因此 dijkstra 算法失效
dijkstra详细步骤
初始dist[1] = 0
找到了未标识且离源点1最近的结点1,标记1号点,用1号点更新其他所有点的距离,2号点被更新成dist[2] = 2,3号点被更新成dist[3] = 5
找到了未标识且离源点1最近的结点2,标识2号点,用2号点更新其他所有点的距离,4号点被更新成dist[4] = 4
找到了未标识且离源点1最近的结点4,标识4号点,用4号点更新其他所有点的距离,5号点被更新成dist[5] = 5
找到了未标识且离源点1最近的结点3,标识3号点,用3号点更新其他所有点的距离,4号点被更新成dist[4] = 3
结束
得到1号点到5号点的最短距离是5,对应的路径是1 -> 2 -> 4 -> 5,并不是真正的最短距离
什么是bellman - ford算法?
Bellman - ford 算法是求含负权图的单源最短路径的一种算法,效率较低,代码难度较小。其原理为连续进行松弛,在每次松弛时把每条边都更新一下,若在 n-1 次松弛后还能更新,则说明图中有负环,因此无法得出结果,否则就完成。
(通俗的来讲就是:假设 1 号点到 n 号点是可达的,每一个点同时向指向的方向出发,更新相邻的点的最短距离,通过循环 n-1 次操作,若图中不存在负环,则 1 号点一定会到达 n 号点,若图中存在负环,则在 n-1 次松弛后一定还会更新)
bellman - ford算法的具体步骤
for n次
for 所有边 a,b,w (松弛操作)
dist[b] = min(dist[b],back[a] + w)
注意:back[] 数组是上一次迭代后 dist[] 数组的备份,由于是每个点同时向外出发,因此需要对 dist[] 数组进行备份,若不进行备份会因此发生串联效应,影响到下一个点
在下面代码中,是否能到达n号点的判断中需要进行if(dist[n] > INF/2)判断,而并非是if(dist[n] == INF)判断,原因是INF是一个确定的值,并非真正的无穷大,会随着其他数值而受到影响,dist[n]大于某个与INF相同数量级的数即可
#include
using namespace std;
const int N=510,M=10010;
int dist[N],back[N];
int n,m,k;
struct edge{
int a,b,w;
}edges[M];
void b(){
memset(dist,0x3f,sizeof dist);
dist[1]=0;
for(int i=1;i<=k;i++){
memcpy(back,dist,sizeof dist);
for(int j=1;j<=m;j++){
int a=edges[j].a,b=edges[j].b,w=edges[j].w;
dist[b]=min(dist[b],back[a]+w);
}
}
/*if (dist[n] > 0x3f3f3f3f / 2) return -1;
return dist[n];*/
//这种写法忽略了最短距离可能为-1的情况,新增数据卡掉了这种情况,不能直接返回-1进行判断。
}
int main(){
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
edges[i]={a,b,c};
}
/*int t = bellman_ford();
if (t == -1) puts("impossible");
else printf("%d\n", t);*/
b();
if(dist[n]>0x3f3f3f3f/2) cout<<"impossible";
else cout < spfa 1//bf优化
Bellman_ford算法会遍历所有的边,但是有很多的边遍历了其实没有什么意义,我们只用遍历那些到源点距离变小的点所连接的边即可,只有当一个点的前驱结点更新了,该节点才会得到更新;因此考虑到这一点,我们将创建一个队列每一次加入距离被更新的结点。
1) st数组的作用:判断当前的点是否已经加入到队列当中了;已经加入队列的结点就不需要反复的把该点加入到队列中了,就算此次还是会更新到源点的距离,那只用更新一下数值而不用加入到队列当中。
即便不使用st数组最终也没有什么关系,但是使用的好处在于可以提升效率。
2) SPFA算法看上去和Dijstra算法长得有一些像但是其中的意义还是相差甚远的:
1] Dijkstra算法中的st数组保存的是当前确定了到源点距离最小的点,且一旦确定了最小那么就不可逆了(不可标记为true后改变为false);SPFA算法中的st数组仅仅只是表示的当前发生过更新的点,且spfa中的st数组可逆(可以在标记为true之后又标记为false)。顺带一提的是BFS中的st数组记录的是当前已经被遍历过的点。
2] Dijkstra算法里使用的是优先队列保存的是当前未确定最小距离的点,目的是快速的取出当前到源点距离最小的点;SPFA算法中使用的是队列(你也可以使用别的数据结构),目的只是记录一下当前发生过更新的点。
3) ⭐️Bellman_ford算法里最后return-1的判断条件写的是dist[n]>0x3f3f3f3f/2;而spfa算法写的是dist[n]==0x3f3f3f3f;其原因在于Bellman_ford算法会遍历所有的边,因此不管是不是和源点连通的边它都会得到更新;但是SPFA算法不一样,它相当于采用了BFS,因此遍历到的结点都是与源点连通的,因此如果你要求的n和源点不连通,它不会得到更新,还是保持的0x3f3f3f3f。
4) ⭐️ Bellman_ford算法可以存在负权回路,是因为其循环的次数是有限制的因此最终不会发生死循环;但是SPFA算法不可以,由于用了队列来存储,只要发生了更新就会不断的入队,因此假如有负权回路请你不要用SPFA否则会死循环。
5) ⭐️由于SPFA算法是由Bellman_ford算法优化而来,在最坏的情况下时间复杂度和它一样即时间复杂度为 O(nm)O(nm) ,假如题目时间允许可以直接用SPFA算法去解Dijkstra算法的题目。(好像SPFA有点小小万能的感觉?)
6) ⭐️求负环一般使用SPFA算法,方法是用一个cnt数组记录每个点到源点的边数,一个点被更新一次就+1,一旦有点的边数达到了n那就证明存在了负环。
作者:orzorz
链接:https://www.acwing.com/solution/content/9306/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
#include
using namespace std;
const int N=1e6+10;
int n,m;
int h[N],e[N],ne[N],idx,w[N],dist[N];
bool st[N];
void add(int a,int b,int c){
e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}
void spfa(){
memset(dist,0x3f,sizeof dist);
dist[1]=0;
queue q;
q.push(1);
st[1]=true;
while(q.size()){
int t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]>dist[t]+w[i]){
dist[j]=dist[t]+w[i];
if(st[j]==false) {
q.push(j);
st[j]=true;
}
}
}
}
/*if(dist[n]>0x3f3f3f/2) return -1;
else return dist[n];*/
//和bellman - ford一样的坑,可能会出现-1的情况
}
int main(){
cin>>n>>m;
memset(h,-1,sizeof(h));
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
/*int t=spfa();
if(t==-1) cout<<"impossible"<1e9) cout<<"impossible"< spfa 2 判断负环
y总的原话
每次做一遍spfa()一定是正确的,但时间复杂度较高,可能会超时。初始时将所有点插入队列中可以按如下方式理解:
在原图的基础上新建一个虚拟源点,从该点向其他所有点连一条权值为0的有向边。那么原图有负环等价于新图有负环。此时在新图上做spfa,将虚拟源点加入队列中。然后进行spfa的第一次迭代,这时会将所有点的距离更新并将所有点插入队列中。执行到这一步,就等价于视频中的做法了。那么视频中的做法可以找到负环,等价于这次spfa可以找到负环,等价于新图有负环,等价于原图有负环。得证。
1、dist[x] 记录虚拟源点到x的最短距离
2、cnt[x] 记录当前x点到虚拟源点最短路的边数,初始每个点到虚拟源点的距离为0,只要他能再走n步,即cnt[x] >= n,则表示该图中一定存在负环,由于从虚拟源点到x至少经过n条边时,则说明图中至少有n + 1个点,表示一定有点是重复使用
3、若dist[j] > dist[t] + w[i],则表示从t点走到j点能够让权值变少,因此进行对该点j进行更新,并且对应cnt[j] = cnt[t] + 1,往前走一步
注意:该题是判断是否存在负环,并非判断是否存在从1开始的负环,因此需要将所有的点都加入队列中,更新周围的点(为解决下图情况)
#include
using namespace std;
const int N=1e6+10;
int n,m;
int h[N],e[N],ne[N],idx,w[N],dist[N];
bool st[N];
int cnt[N];
void add(int a,int b,int c){
e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}
bool spfa(){
memset(dist,0x3f,sizeof dist);
dist[1]=0;
queue q;
for(int i=1;i<=n;i++){
q.push(i);
st[i]=true;
}
while(q.size()){
int t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]>dist[t]+w[i]){
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n) return true;
if(st[j]==false) {
q.push(j);
st[j]=true;
}
}
}
}
return false;
}
int main(){
cin>>n>>m;
memset(h,-1,sizeof(h));
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
if (spfa()) puts("Yes");
else puts("No");
return 0;
} Floyd求最短路
#include
using namespace std;
int a[205][205],n,m,K;
int main(){
cin>>n>>m>>K;
memset (a,0x3f,sizeof(a));
for(int i=1;i<=n;i++) a[i][i]=0;
for(int i=1;i<=m;i++){
int x,y,c;
cin>>x>>y>>c;
if(a[x][y]>c) a[x][y]=c;//处理自环
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
a[i][j]=min(a[i][j],a[i][k]+a[k][j]);//判断通过k中转是否会更近
}
}
}
for(int i=1;i<=K;i++){
int x,y;
cin>>x>>y;
if(a[x][y]>=2e6) cout<<"impossible"< Kruskal算法求最小生成树s
算法流程
- 建立并查集,每个点各自构成一个集合
- 把所有边按照权值从小到大排序,依次扫描每条边(x,y,z)
- 若x,y属于同一个集合(连通),则忽略这条边继续扫描下一条
- 否则,合并x,y所在的集合,并把z累加到答案中
- 所有便扫描完成后,第四步中处理过的边就构成最小生成树
#include
using namespace std;
const int N=2e5+10,INF = 0x3f3f3f3f;
int n,m;
int p[N];
int find(int x){
if(p[x]!=x){
p[x]=find(p[x]);
}
return p[x];
}
struct st{
int a,b,w;
};
st e[N];
bool cmp(st a,st b){
return a.w