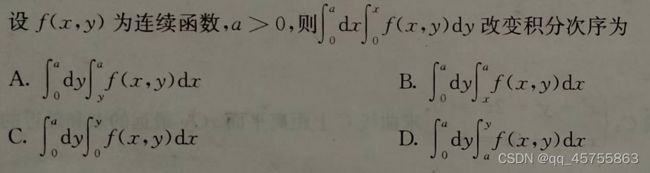专转本-数学（含线性代数）难点
- 微分中值定理
——罗尔中值定理
习题： g ( x ) = x ( x + 1 ) ( 2 x + 1 ) ( 3 x − 1 ) , 则 方 程 g ′ ( x ) = 0 ， 在 ( − 1 , 0 ) 内 的 实 根 的 个 数 恰 为 ( B ) g(x)=x(x+1)(2x+1)(3x-1),则方程g'(x)=0，在(-1,0)内的实根的个数恰为(B) g(x)=x(x+1)(2x+1)(3x−1),则方程g′(x)=0，在(−1,0)内的实根的个数恰为(B)
A.1 B.2 C.3 D.4
——拉格朗日中值定理
-
二重积分坐标转换
将 ∫ 0 2 d x ∫ x 3 x f ( x 2 + y 2 ) d y 化 为 极 坐 标 下 的 二 次 积 分 为 ∫ π 4 π 3 d θ ∫ 0 2 s e c x f ( ρ ) ρ d ρ ‾ 将\int_{0}^{2}dx\int _{x}^{\sqrt{3}x}f(\sqrt{x^2+y^2})dy化为极坐标下的二次积分为\underline{\int_{\frac{π}{4}}^{\frac{π}{3}}d\theta\int _{0}^{2secx}f(\rho)\rho d\rho} 将∫02dx∫x3xf(x2+y2)dy化为极坐标下的二次积分为∫4π3πdθ∫02secxf(ρ)ρdρ
-
幂级数展开幂级数
下列级数中条件收敛的是(A)
A. ∑ n = 1 ∞ ( − 1 ) n n n 2 + 1 \sum_{n=1}^{\infty}\frac{(-1)^nn}{n^2+1} ∑n=1∞n2+1(−1)nn
B . ∑ n = 1 ∞ ( − 1 ) n n n + 1 B.\sum_{n=1}^{\infty}\frac{(-1)^nn}{n+1} B.∑n=1∞n+1(−1)nn
C . ∑ n = 1 ∞ ( − 1 ) n n n 2 + 1 C.\sum_{n=1}^{\infty}\frac{(-1)^nn}{n^2+1} C.∑n=1∞n2+1(−1)nn
lim n → ∞ u n ≠ 0 发 散 \lim_{n \to \infty}{u_n \not =0}发散 limn→∞un=0发散
D . ∑ n = 1 ∞ ( − 1 ) n n ! 2 n D.\sum_{n=1}^{\infty}\frac{(-1)^nn!}{2^n} D.∑n=1∞2n(−1)nn!
-
二重积分改变积分次序
-
变上限积分
-
莱布尼茨公式
莱布尼茨定定理：
交 错 级 数 ∑ n = 1 ∞ ( − 1 ) n − 1 u n ( u n ≥ 0 ) 满 足 条 件 ： u n ≥ u n + 1 lim n → ∞ u n = 0 , 那 么 级 数 收 敛 交错级数\sum_{n=1}^{\infty}(-1)^{n-1}u_n~~~(u_n\geq 0)满足条件：u_n \geq u_{n+1} \lim_{n \to \infty}u_n=0,那么级数收敛 交错级数n=1∑∞(−1)n−1un (un≥0)满足条件：un≥un+1n→∞limun=0,那么级数收敛下题的交错级数就用到了莱布尼茨定理
-
函数的极值、驻点、基本概念
设 f ( x ) = 2 x 5 3 − 5 x 2 3 , 则 函 数 f ( x ) （ C ） 设f(x)=2x^{\frac{5}{3}}-5x^{\frac{2}{3}},则函数f(x) （ C ） 设f(x)=2x35−5x32,则函数f(x)（C）
A.只有一个最大值 B.只有一个最小值 C.既有极大值又有极小值 D.没有极值 -
线性相关、无关、线性表示、基础解析、通解
线性相关：在向量空间V的一组向量A: ，如果存在不全为零的数 k1, k2, ···,km , 使的则称向量组A是线性相关的 ,否则称它是线性无关
设四阶矩阵A不可逆， a 12 的 代 数 余 子 式 ∣ A 1 ∣ ≠ 0 , α 1 , α 2 , α 3 , α 4 为 矩 阵 的 列 向 量 组 , A ∗ 是 A 的 伴 随 矩 阵 , 那 么 A ∗ x = 0 的 通 解 是 （ ） a_{12}的代数余子式|A_{1}|\not=0,α_{1},α_{2},α_{3},α_{4}为矩阵的列向量组,A^*是A的伴随矩阵,那么A^*x=0的通解是（） a12的代数余子式∣A1∣=0,α1,α2,α3,α4为矩阵的列向量组,A∗是A的伴随矩阵,那么A∗x=0的通解是（）
9. 微分方程已知特解求通解
- 多元函数求极值
- 行列式的基本运算法则
设 α 1 = ( 1.4 , 0 , 2 , α 2 = ( 2 , 7 , 1 , 3 ) , α 3 = ( 0 , 1 , 一 1 , 2 ) , α 3 = ( 3 , 10 ， a , 4 ） , 问 a 取 何 值 时 , β 可 由 α 1 , α 2 , α 3 线 性 表 示 ? 并 写 出 表 达 式 设α_1=(1.4,0,2,α_2 = (2,7,1,3),α_3 = (0,1,一1,2),α_3=(3,10，a,4）,问a取何值时,β可由α_1,α_2,α_3线性表示?并写出表达式 设α1=(1.4,0,2,α2=(2,7,1,3),α3=(0,1,一1,2),α3=(3,10，a,4）,问a取何值时,β可由α1,α2,α3线性表示?并写出表达式
- 构造拉个朗日函数
- 幂级数展开
将 函 数 f ( x ) = 1 x 2 − 2 x − 3 展 开 为 x 的 幂 级 数 将函数f(x) = \frac{1}{x^2-2x-3}展开为x的幂级数 将函数f(x)=x2−2x−31展开为x的幂级数
