DFS深度优先搜索算法(适合初学者)
前言
本文旨在帮助小白熟悉DFS的基本流程和递归算法的理解,主要包括我们用回溯的思想对题目进行分析的过程,编写代码过程中递归函数语义以及参数的确定等一系列细节。
基本的概念
官方解释:一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件,搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。
其实说白了就跟咱们闯关游戏一样,遇到分岔路然后我们选一条路走到头结果发现不是终点,我们则需要重新返回到分岔路进行重新选择。
从上面我们可以提炼出来基本模板
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
路径:你已经选择的道路。
选择列表:岔路口可选择的道路。
做选择:在岔路口做道路的选择。
撤销操作:发现此路不通,返回最近的岔路口,选其它的道路。代码模块不唯一,选择自己可以理解的即可,上面的代码模板主要借鉴labuladong的文章
下面咱们就以全排列、组合为例,一起来深入理解DFS算法和递归算法。
全排列问题
问题分析:
1、首先要搞清题目,知道全排列是什么意思。
2、根据题目我们可以画出相应的树结构
注意:画图可以更加清晰的捋清我们的思路,如果直接跳入递归很容易混淆。
接下来我们试着带入一下模板里面:1、如果先选择路径为[1] ,
2、剩余可选择的有[2,3],
3、继续选择下一条道路,并记录已走过的路径[1,2]
4、如果不需要选择,则直接添加[3]。返回路径[1,2,3]
5、返回到最近的岔路口,选择其它道路重复上述过程
3、确定递归函数的语义以及参数
这一步对初学者来说应该是比较有难度的,对递归函数语义的掌握不是一蹴而就的,需要经验的积累才能熟练。一般递归函数的语义往往都是来根据题目要求决定的。本题要求我们求出不重复的全排列组合,所以我们的语义就为:给我一组数,返回一个没有重复数字的排列数组。
还有人对参数的选择比较迷茫,一句话变量就是会变的量。就本题来说会变的量无非就是可选择的路径和记录的路径
4、代码分析
class Solution {
List>res =new LinkedList<>();
public List> permute(int[] nums) {
LinkedListtrack=new LinkedList<>(); //记录路径
backtrack(nums,track);
return res;
}
void backtrack(int []nums,LinkedListtrack)
{
if(track.size()==nums.length) //结束条件,所有数字都排列完毕
{
res.add(new LinkedList(track));
return;
}
for(int i=0;i 初学者建议先把树状图和代码对应起来,自己画一下递归的过程,帮助自己理解!!!
组合问题
问题分析:
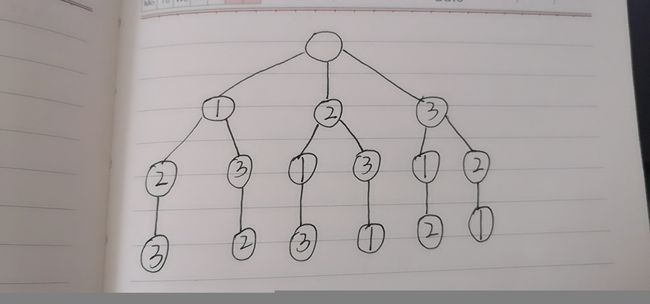
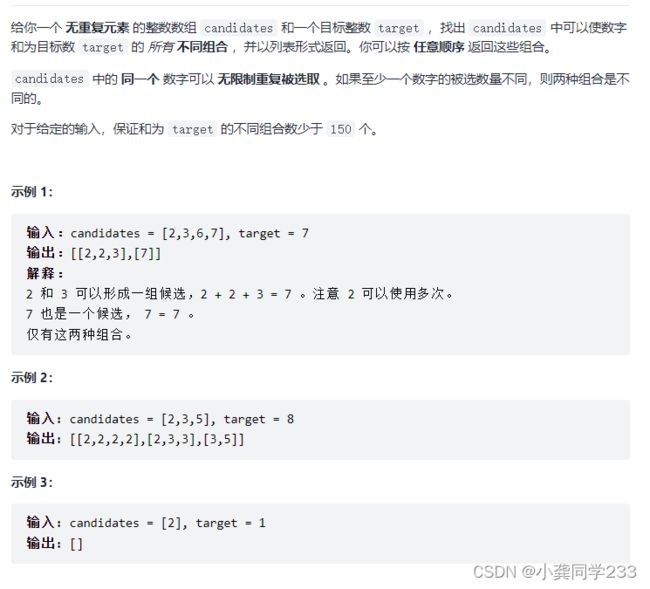
1、搞清题目要求,我们可以发现同一个组合内数字不可以重复,组合之间不能重复(可以为剪枝提供思路)
2、画图
通过图我们可以发现,因为题目给的是非递减的数组,所以我们的选择列表从当前数的后一位开始的方式,进行剪枝操作,解决了题目要求。
3、确定递归函数的语义以及参数
语义:给我一组数和限制长度K,返回一个没有重复数字且长度为K的排列数组。
参数:[1-n]的数,限制长度K,实现选择列表从当前数后一位的标记start,存储结果的数组
4、代码分析
class Solution {
List>res=new LinkedList<>();
public List> combine(int n, int k) {
if(k<=0||n<=0)//特殊情况直接结束
{
return res;
}
LinkedListtrack=new LinkedList<>();
backtrack(n,k,1,track);
return res;
}
void backtrack(int n,int k,int start, LinkedListtrack)
{
if(k==track.size())//结束条件,选择了k个不重复的数
{
res.add(new LinkedList(track)); //返回结果
return;
}
for(int i=start;i<=n;i++) //剪枝操作,每次从start后开始选择,避免数字和组合重复问题
{
track.add(i); //做选择
backtrack(n,k,i+1,track); //递归进入下一个岔路口
track.removeLast(); //撤销,返回最近的岔路口
}
}
} 总结:
DFS算法和递归都是比较抽象的,一定要先画图理解,直接手撕代码很容易把自己劝退的。递归函数的语义和参数选择部不熟的,可以看看别人的优秀代码,学习人家的思路。
---------------------------------------------------------------------------------------------------------------------------------
上面是一道很典型的回溯问题,大家可以上手试一试,在评论区留下自己的递归函数