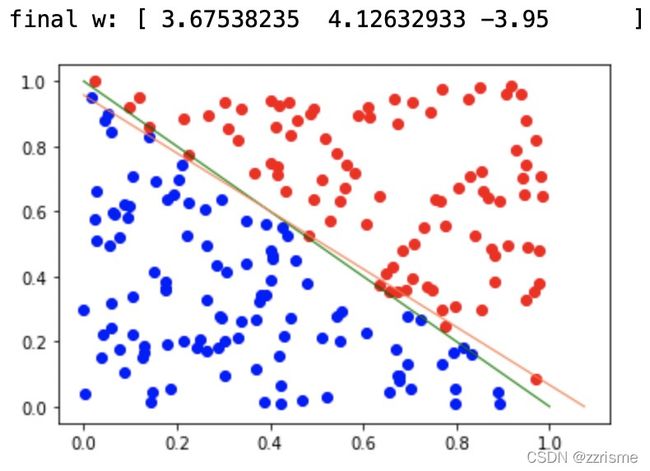
用随机梯度下降法实现 SVM 线性分类器的实例

本文使用自己编写的例子来帮助理解用随机梯度下降法（Stochastic Gradient Descent）实现 SVM 线性分类器，不会过多涉及理论和原理的分析，只是为了更形象的理解。例子中使用的是二维平面。

问题：
给定一组训练数据 $(x_i,y_i)$，$x_i\in {\mathbb{R}}^n$ 表示数据的特征，$y_i\in \{+1,-1\}$ 表示数据的标记。对于其中一部分特征的 $x_i$，对应的标记 $y_i=1$，另一部分特征的 $x_i$，对应的标记 $y_i=-1$，我们的目的是想要找到一个线性分类函数 $f(x_i)$，使得：
$$f(x_i)\{\begin{array}{r}\ge 0,y_i=+1\\ <0,y_i=-1\end{array}$$

例如：满足 $y_{i}f(x_i)>0$ 的$f(x_i)$ 就是一个合格的分类函数

只考虑二维平面，因为是线性分类函数，所以是一条直线：
$$f(x)=w_1{x}_1+w_2{x}_2+b=0$$
一般形式是：$f(x)=w^{T}x+b=0$
假设离这条直线最近的两个正负分类的点分别是 $x_{+}$ 和 $x_{\_}$，如果把这条直线放在它们的中间位置，我们当然希望它们离直线的距离越大越好，如果 $x_{+}$ 的坐标是$(x_1,x_2)$，那么它离直线的距离就是：
$$\frac{w_1{x}_1+w_2{x}_2+b}{\sqrt{w_1^2+w_2^2}}$$
记$u=w_1{x}_1+w_2{x}_2+b$，我们取:
$$\begin{gathered} v_1=w_1/u \\ {v}_2=w_2/u \\ d=b/u \\ g(x)=v_1{x}_1+v_2{x}_2+d \end{gathered}$$
可以知道 $f(x)=0$ 和 $g(x)=0$ 是同一条直线，但上述的距离就变成：
$$\frac{v_1{x}_1+v_2{x}_2+d}{\sqrt{v_1^2+v_2^2}}=\frac{(w_1{x}_1+w_2{x}_2+b)/u}{\sqrt{v_1^2+v_2^2}}=\frac{1}{\sqrt{v_1^2+v_2^2}}=\frac{1}{\Vert v\Vert }$$
我们希望 $x_{+}$ 和 $x_{\_}$ 离直线的距离最大，也就是希望：
$$\max \frac{2}{\Vert v\Vert }$$
等同于:
$$\min \Vert v{\Vert }^2\text{ subject to }{y}_i(v{x}_i+d)\ge 1\text{ for }i=1...N$$
为了方便，我们还是记成：
$$\min \Vert w{\Vert }^2\text{ subject to }{y}_i(w{x}_i+b)\ge 1\text{ for }i=1...N$$
实际情况中，我们可能遇到无法线性可分，或者有误差的情况，所以为了取得较好的分类效果，我们允许有例外的发生，于是引入松弛变量${\xi }_i$：
$$\min \Vert w{\Vert }^2+C\sum {\xi }_i$$
subject to
$$y_i(w{x}_i+b)\ge 1-{\xi }_i\text{ or }{y}_{i}f(x_i)\ge 1-{\xi }_i$$
也就是说，我们允许有个别点到分类直线的距离小于之前规定的值（当$0<{\xi }_i<1$），甚至允许个别点的分类是错的（当${\xi }_i>1$），比如样本误差。这样做是为了换取更好的分类效果。

较大的 $C$ 表示取消松弛变量，因为任何一点点微小的 ${\xi }_i$ 都将招致严厉的惩罚；反之，较小 $C$ 则表示宽松的松弛变量，允许误差。
既然约束要求 ${\xi }_i\ge 0$ 且 ${\xi }_i\ge 1-y_{i}f(x_i)$，那么我们取 ${\xi }_i=\max (0,1-y_{i}f(x_i))$ 就可以满足约束，因此可以把一个约束问题变成一个无约束问题：
$$\min \Vert w{\Vert }^2+C\sum \max (0,1-y_{i}f(x_i))$$
上式是我们要优化的目标函数，前半部分是“正则化”，后半部分是“损失函数”。对于损失函数来说，那些 $y_{i}f(x_i)>1$ 的点是分类效果比较好的点，取值0，无需贡献损失；那些 $y_{i}f(x_i)<1$ 的点是分类效果比较差的点，甚至是错误分类的点，会贡献损失，我们希望这个损失越小越好。

接下来是一些理论部分，不深入。简单来说，目标函数由正则化和损失函数组成，正则化和损失函数都是凸函数（convex），因此目标函数也是凸函数，对于 min 存在唯一最优解，且局部最优解就是全局最优解，因此非常适合用梯度下降法进行求解。

另一方面，当前我们要优化的目标函数包含了所有的样本 $(x_i,y_i)$ ，如果数量很大，势必对计算性能是很大的考验，所以我们引入了“随机”（stochastic）的思想，每次迭代只选择随机的一部分样本参与计算，因此我们使用平均的方式来重写上述目标函数：
$$\begin{gathered} C(w)=\Vert w{\Vert }^2+C\sum \max (0,1-y_{i}f(x_i)) \\ =\frac{1}{NC}\Vert w{\Vert }^2+\frac{1}{N}\sum \max (0,1-y_{i}f(x_i))\text{ （整体除以NC）} \\ =\frac{2}{NC}\frac{1}{2}\Vert w{\Vert }^2+\frac{1}{N}\sum \max (0,1-y_{i}f(x_i))\text{ （加个1/2，求导好看些）} \\ =\frac{\lambda }{2}\Vert w{\Vert }^2+\frac{1}{N}\sum \max (0,1-y_{i}f(x_i))(\lambda =\frac{2}{NC}) \\ =\frac{1}{N}\sum (\frac{\lambda }{2}\Vert w{\Vert }^2+\max (0,1-y_{i}f(x_i))) \end{gathered}$$
GeeksforGeeks 网站关于“随机”的介绍

The word ‘stochastic‘ means a system or a process that is linked with a random probability. Hence, in Stochastic Gradient Descent, a few samples are selected randomly instead of the whole data set for each iteration.

这里的损失函数是不可微的（not differentiable），所以要计算的是次梯度（sub-gradient）。
$$\begin{gathered} \nabla C(w)=\nabla \frac{1}{N}\sum (\frac{\lambda }{2}\Vert w{\Vert }^2+\max (0,1-y_{i}f(x_i))) \\ =\nabla \frac{1}{N}\sum (\frac{\lambda }{2}\Vert w{\Vert }^2+\max (0,1-y_i(w{x}_i+b))) \\ =\{\begin{array}{lc}\frac{1}{N}\sum (\lambda w-y_i{x}_i)& \text{ if }{y}_{i}f(x_i)<1\\ \frac{1}{N}\sum \lambda w& \text{ if }{y}_{i}f(x_i)\ge 1\end{array} \\ =\{\begin{array}{lc}\lambda w-\mathbb{E}(y_i{x}_i)& \text{ if }{y}_{i}f(x_i)<1\\ \lambda w& \text{ if }{y}_{i}f(x_i)\ge 1\end{array} \end{gathered}$$
因此，每一次迭代就是（$\eta$ 是步长）：
$$w_{t+1}=\{\begin{array}{lc}{w}_t-\eta (\lambda w_t-\mathbb{E}(y_i{x}_i))& \text{ if }{y}_{i}f(x_i)<1\\ w_t-\eta \lambda w_t& \text{ if }{y}_{i}f(x_i)\ge 1\end{array}$$

最后我们来实现它，讲解一下我自己写的 Python 代码：

from matplotlib import pyplot as plt
import numpy as np
import random
import time
def sgd_svm(x,y,opts): #使用 Stochastic Gradient Descent 算法实现 SVM 的函数
    start_time = time.time() #记录开始时间
    max_count = opts[0] #取迭代次数
    C = opts[1] #取 C 值
    D = x.shape[0] #取 x 的行数作为维数
    N = x.shape[1] #取 x 的列数作为样本数
    w = np.zeros(D) #初始 w1 和 w2 取 0，1 行 2 列
    b = 0;
    w = np.append(w,b) #初始 w0 取 0，w 变成 1 行 3 列
    x = np.append(x,[np.ones(N)],axis=0) #x 添加第三行，都取 1，表示和 w0 相乘的部分。
    sample_num = int(0.001 * N) #确定采样数量
    sample_list = [s for s in range(N)] #生成全数据索引表 1～N
    for j in range(1,max_count): #开始迭代
        sample_list = random.sample(sample_list,sample_num) #随机采样索引表
        sample_x = x[:,sample_list] #生成采样 x 数据
        sample_y = y[sample_list] #生成采样 y 数据
        '''
        求 kexi，1 行 n 列，表示每个点的 max(0, 1-yif(xi))值，
        有的是 0，有的是正数，正数表示在当前迭代的 w 下分类效果很差的点
        '''
        kexi = np.maximum(np.zeros(sample_num),np.ones(sample_num)-sample_y*(w@sample_x))
        '''
        计算 w1 和 w2 的梯度，结果是 1 行 2 列，
        y[np.nonzero(kexi)[0]] 表示 kexi 中那些非 0 的坐标对应的 y 中的值
        （+1 或者 -1，坐标表示在当前迭代的 w 下分类效果很差的点），结果是 1 行 多 列；
        x[0:D,np.nonzero(kexi)[0]].T 表示 kexi 中那些非 0 的坐标对应的 x 中的值
        （x1 和 x2，坐标表示在当前迭代的 w 下分类效果很差的点），结果是 2 行 多列，因此需要转置，
        @ 表示矩阵乘法，得到 1 行 2 列。
        '''
        g = w[0:D]*2/(sample_num*C)-(sample_y[np.nonzero(kexi)[0]]@sample_x[0:D,np.nonzero(kexi)[0]].T)/sample_num
        '''
        计算 w0 的梯度，结果是 1 行 1 列，
        y[np.nonzero(kexi)[0]] 表示 kexi 中那些非 0 的坐标对应的 y 中的值
        （+1 或者 -1，坐标表示在当前迭代的 w 下分类效果很差的点），结果是 1 行 多 列；
        x[D,np.nonzero(kexi)[0]].T 表示 kexi 中那些非 0 的坐标对应的 x 中 1 的值
        （x0 都是 1，坐标表示在当前迭代的 w 下分类效果很差的点），1 行 多列，因此需要转置，
        @ 表示矩阵乘法，得到 1 行 1 列。
        '''
        g1 = -(sample_y[np.nonzero(kexi)[0]]@sample_x[D,np.nonzero(kexi)[0]].T)/sample_num
        g = np.append(g,g1) #把 w0 添加到 w1 和 w2 的后面，结果是 1 行 3 列
        w = w-g #用负梯度方向迭代 w，结果是 1 行 3 列
    end_time = time.time() #记录结束时间
    print('Took %f second' % (end_time - start_time)) #打印运行时间
    return w #返回 w
num = 200000
x = np.random.rand(2,num) #在取值(0,1)范围内，生成二维坐标 200 个，结果是 2 行 200 列
y = np.zeros(num) #y 是分类结果，初始填 0，1 行 200 列
i = 0
while i < num :
    if x[0,i]+x[1,i]-1 > 0:
        #plt.scatter(x[0,i], x[1,i], c='r')
        y[i]=1 #如果该点在 x1 + x2 - 1 = 0 直线上方，画红点，对应的 y 取 +1
    else:
        #plt.scatter(x[0,i], x[1,i], c='b')
        y[i]=-1 #如果该点在 x1 + x2 - 1 = 0 直线下方，画蓝点，对应的 y 取 -1
    i=i+1
plt.plot([1,0], [0,1], linewidth=1, color='green') #画出理想的分类直线
opts=(10000,100) #优化参数，第一项表示迭代次数，第二项表示 C 的值
w = sgd_svm(x,y,opts) #调用函数
print("final w:",w) #打印最优解[w1, w2, w0]
plt.plot([-w[2]/w[0],0], [0,-w[2]/w[1]], linewidth=1, color='coral') #画出求解的分类直线
plt.show() #打印图片

这是运行结果：

看起来还不错。

这是 MATLAB 版本的（没有做采样）：

function [w]=svm_ssd(X,y,opts)
%X是学习数据，行是维度，列是个数
N=size(X,2);
D=size(X,1);
MAX_COUNT=opts(1);
%迭代次数
C=opts(2);
w=zeros(1,D)';
b=0;
X=[X;ones(1,N)];
w=[w;b];
for i=1:MAX_COUNT
    kexi=max(zeros(1,N),ones(1,N)-y.*(w'*X));
    %kexi是一行向量，列对应每一个点求出的max(0,1-yif(xi))
    g=w(1:D,:)*2/(N*C)-(y(:,find(kexi~=0))*X(1:D,find(kexi~=0))'/N)';
    %find用来找到max不为0的指标（列坐标）X和y相乘后就是西格玛求和了，所以再除以N
    %减法的前半部分是w二范数的梯度，后半部分是max求和再除以N的梯度
    g(D+1)=-y(:,find(kexi~=0))*X(D+1,find(kexi~=0))'/N;
    w=w-g;
end
w=w/w(1);
end