字符串匹配算法(C/Java实现)

BF算法

BF算法，即暴力(Brute Force)算法，是普通的模式匹配算法，BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和 T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果。

该算法最坏情况下要进行M*(N-M+1)次比较，时间复杂度为O(MN)。

C语言实现

#define _CRT_SECURE_NO_WARNINGS
#include
#include 
#include
//字符串匹配算法 BF KMP
//str 主串  sub 子串
//返回值：返回子串在主串中的下标，如果不存在就返回-1
int BF(char* str,char* sub)
{
	assert(str != NULL && sub != NULL);
	if (str == NULL || sub == NULL)
	{
		return -1;
	}
	int lenStr = strlen(str);
	int lenSub = strlen(sub);
	int i = 0;
	int j = 0;
	while (i < lenStr && j < lenSub)
	{
		if (str[i] == sub[j])
		{
			i++;
			j++;
		}
		else
		{
			i = i - j + 1;
			j = 0;
		}
	}
	if (j >= lenSub)//j走完了子串
	{
		return i - j;
	}
	return -1;
}
int main()
{
	printf("%d\n", BF("ababcabcdabcde", "abcd"));//5
	printf("%d\n", BF("ababcabcdabcde", "abcdef"));//-1
	printf("%d\n", BF("ababcabcdabcde", "ab"));//0
	return 0;
}

Java实现

public class Test {
    public static int BF(String str,String sub){
        if(str==null||sub==null){
            return -1;
        }
        int lenStr=str.length();
        int lenSub=sub.length();
        if(lenStr==0||lenSub==0){
            return -1;
        }
        int i=0;//遍历主串
        int j=0;//遍历子串
        while(i<lenStr&&j<lenSub){
            if(str.charAt(i)==sub.charAt(j)){
                i++;
                j++;
            }else{
                i=i-j+1;
                j=0;
            }
        }
        if(j>=lenSub){
            return i-j;
        }
        return -1;
    }
    public static void main(String[] args) {
        System.out.println(BF("ababcabcdabcde","abcd"));//5
        System.out.println(BF("ababcabcdabcde","abcdef"));//-1
        System.out.println(BF("ababcabcdabcde","ab"));//0

    }
}

KMP算法

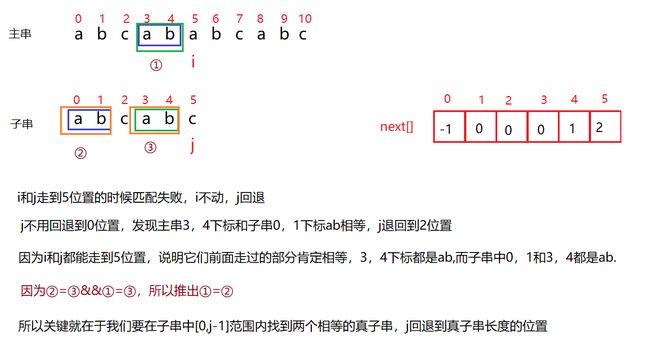
KMP算法是一种改进的字符串匹配算法。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。

为了减少匹配次数，匹配失败时i，j的回退位置变了

KMP的精髓就是next数组：也就是用next[j]=k来表示。如果匹配失败，子串j要移动到k的位置重新开始匹配。

k的值是这样求的：在范围[0,j-1]内找到匹配成功部分的两个相等的真子串(不包括本身)。k=真子串的长度

不管什么数据，next[0]=-1;next[1]=0;

练习1：对于"ababcabcdabcde",求其next[]数组？

-1 0 0 1 2 0 1 2 0 0 1 2 0 0

(发现0，1，2增加是均匀增加的)

练习2：对“abcabcabcabcdabcde"，求其next[]数组？

-1 0 0 0 1 2 3 4 5 6 7 8 9 0 1 2 3 0

接下来的问题是，已知next[i]=k,怎么求next[i+1]=?

Java实现

public class Test {
    //构建next[]数组
    public static void getNext(int[] next,String sub,int lenSub){
        next[0]=-1;
        next[1]=0;
        int i=2;
        int k=0;
        while(i<lenSub){
            if(k==-1||next[i-1]==next[k]){
                next[i]=k+1;
                i++;
                k++;
            }
            else{
                k=next[k];
            }
        }
    }
    public static int kmp(String str,String sub,int pos){
        if(str==null||sub==null) return -1;
        int lenStr=str.length();
        int lenSub=sub.length();
        if(lenStr==0||lenSub==0) return -1;
        int i=pos;//遍历主串
        int j=0;//遍历子串
        int[] next=new int[lenSub];
        getNext(next,sub,lenSub);
        while(i<lenStr&&j<lenSub){
            if(j==-1||str.charAt(i)==sub.charAt(j)){
                i++;
                j++;
            }
            else{
                j=next[j];//匹配失败回退
            }
        }
        if(j>=lenSub){
            return i-j;
        }
        return -1;
    }
    public static void main(String[] args) {
        System.out.println(kmp("ababcabcdabcde","abcd",0));
        System.out.println(kmp("ababcabcdabcde","abcdf",0));
        System.out.println(kmp("ababcabcdabcde","ab",0));
    }
}

C语言实现

#define _CRT_SECURE_NO_WARNINGS
#include 
#include 
#include 
#include 
void getNext(char* sub, int* next, int lenSub)
{
	next[0] = -1;
	next[1] = 0;
	int i = 2;
	int k = 0;
	while (i < lenSub)
	{
		if (k==-1||sub[i - 1] == sub[k])
		{
			next[i] = k + 1;
			i++;
			k++;
		}
		else
		{
			k = next[k];
		}
	}
}
int KMP(char* str,char* sub,int pos)
{
	assert(str != NULL && sub != NULL);
	int lenStr = strlen(str);
	int lenSub = strlen(sub);
	if (lenStr == 0 || lenSub == 0) return -1;
	int i = pos;//遍历主串
	int j = 0;//遍历字串
	int* next = (int*)malloc(sizeof(int) * lenSub);
	getNext(sub,next,lenSub);
	while (i < lenStr && j < lenSub)
	{
		if (j==-1||str[i] == sub[j])
		{

			i++;
			j++;
		}
		else
		{
			j = next[j];//匹配失败j回退
		}
	}
	if (j >= lenSub)
	{
		return i - j;
	}
    //主串走完了还没匹配成功
	return -1;
}
int main()
{
	printf("%d\n", KMP("ababcabcdabcde","abcd",0));//5
	printf("%d\n", KMP("ababcabcdabcde","abcdf",0));//-1
	printf("%d\n", KMP("ababcabcdabcde","ab",0));//0
	return 0;
}

next[]数组的优化

练习：