李宏毅-机器学习-RNN-笔记

---

前言

李宏毅-机器学习课程-笔记

---

1 RNN

1.1 引例导入

引例：利用前馈神经网络(FFN)解决在空缺位置填充单词问题
\qquad FFN:Input:一个单词（一个向量表示一个单词）
\qquad     Output:输入单词属于空缺位置的概率分布

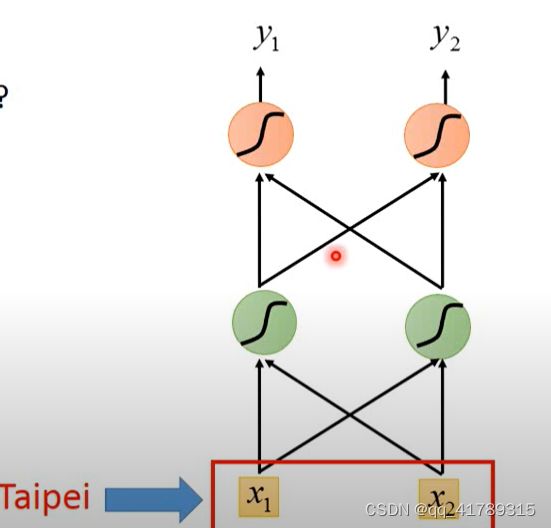
\qquad FNN缺点：神经网络没有记忆力,不考虑上下文,对于不同性质的空缺位置,输入单词的概率分布是相同的。
\qquad 比如：第一句中$Taipei$是目的地,而在第二句中是出发地,那么在这两个空缺的地方,$Taipei$出现的概率不一定是相同的,而利用FNN计算之后$Taipei$的概率分布始终是不变的,不符合语义.

1.2 RNN

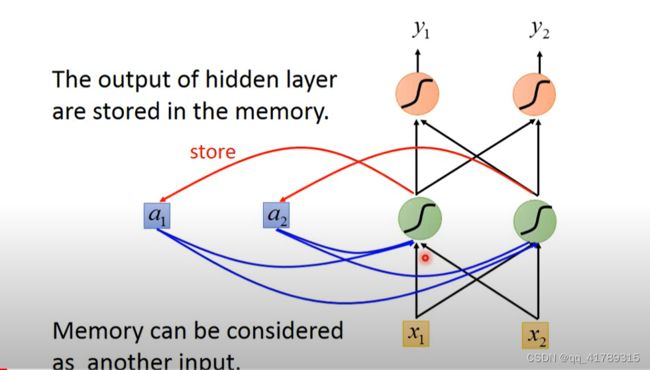
RNN：拥有记忆力,考虑上下文内容,相同输入不同概率分布输出的神经网络;
\qquad  隐藏层的输出存储在内存中,网络的输入不光考虑原始的输入也要考虑隐藏层的输出;
\qquad  换句话说就是将隐藏层的输出同时作为输入,影响输出.

1.3 举例

输入序列：
\qquad \qquad $\left[\begin{array}{c}1\\ 1\end{array}\right]\left[\begin{array}{c}1\\ 1\end{array}\right]\left[\begin{array}{c}2\\ 2\end{array}\right]......$
条件：所有权重$w$均为1;没有偏差$bias$;所有激活函数均为线性函数.

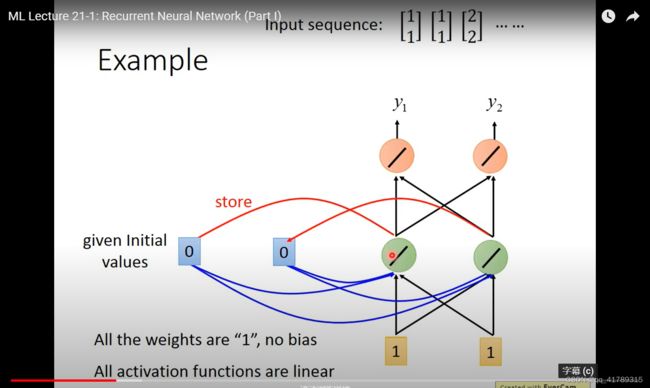
1. 按照上面的网络结构和输入序列，计算输出结果
2. 使用RNN之前必须要给内存中$a_1$ $a_2$初始值,默认为0.
   
   (1) $input:\left[\begin{array}{c}1\\ 1\end{array}\right]$,$\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$,

\qquad   经过网络后$\left[\begin{array}{c}{h}_1\\ h_2\end{array}\right]=\left[\begin{array}{c}2\\ 2\end{array}\right]$,

\qquad   $ouput=\left[\begin{array}{c}4\\ 4\end{array}\right]$,并且将$\left[\begin{array}{c}{h}_1\\ h_2\end{array}\right]$赋值给$\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]$,则$\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]=\left[\begin{array}{c}2\\ 2\end{array}\right]$，并且也作为下一次的输入.

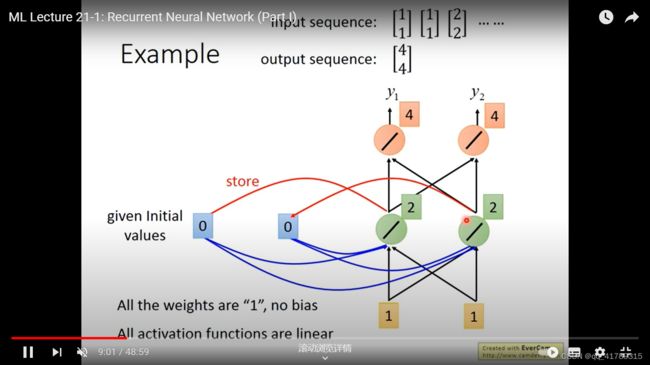
\qquad (2) $input:\left[\begin{array}{c}1\\ 1\end{array}\right]$,$\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]=\left[\begin{array}{c}2\\ 2\end{array}\right]$,

\qquad   经过网络后$\left[\begin{array}{c}{h}_1\\ h_2\end{array}\right]=\left[\begin{array}{c}6\\ 6\end{array}\right]$,

\qquad   $ouput=\left[\begin{array}{c}12\\ 12\end{array}\right]$,并且将$\left[\begin{array}{c}{h}_1\\ h_2\end{array}\right]$赋值给$\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]$,则$\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]=\left[\begin{array}{c}6\\ 6\end{array}\right]$，并且也作为下一次的输入.

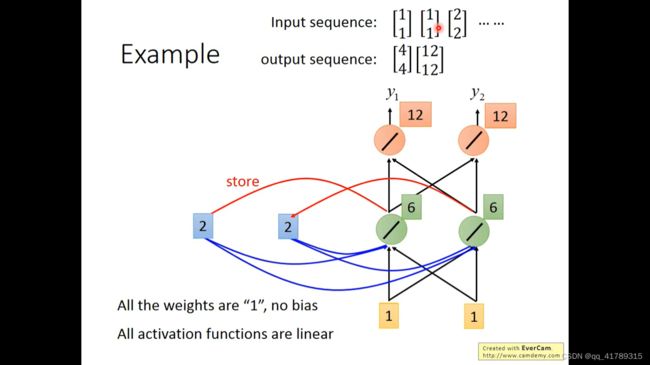
\qquad (3) $input:\left[\begin{array}{c}2\\ 2\end{array}\right]$,$\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]=\left[\begin{array}{c}16\\ 16\end{array}\right]$,

\qquad   经过网络后$\left[\begin{array}{c}{h}_1\\ h_2\end{array}\right]=\left[\begin{array}{c}6\\ 6\end{array}\right]$,

\qquad   $ouput=\left[\begin{array}{c}32\\ 32\end{array}\right]$,并且将$\left[\begin{array}{c}{h}_1\\ h_2\end{array}\right]$赋值给$\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]$,则$\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]=\left[\begin{array}{c}16\\ 16\end{array}\right]$，并且也作为下一次的输入.

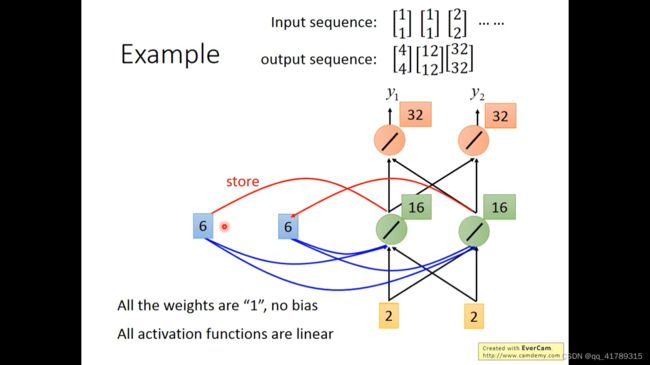
\qquad 如果改变输入序列的顺序就会改变输出结果,说明RNN会考虑输入数据的顺序问题，在预测当前结果时，也包括了之前的信息。
RNN 解决引例问题过程：
\qquad 首先将句子当中的每一个单词转换为向量，例如$arrive=x^1$,将$x^1$放入RNN中得到$a^1$,根据$a^1$得到$y^1$,$y^1$是$arrive$在每一个空缺处的概率分布，$a^1$存储起来，同时与$x^2$作为预测$Taipei$概率分布的输入,说明预测$Taipei$,考虑到了前面是$arrive$的信息,以此类推。
\qquad 图中的网络中并不是3个RNN,而是同一个RNN在不同的时间点,使用3次.

\qquad 所以当$Taipei$前面的单词不同时，那么通过$x^1$计算出来的$a^1$的值也是不同的,作为预测$Taipei$概率的输入也就不同,那么计算出来的概率就是不同的,不同上下文$Taipei$的概率就是不同的。

\qquad 可以将RNN结构设计为深度网络

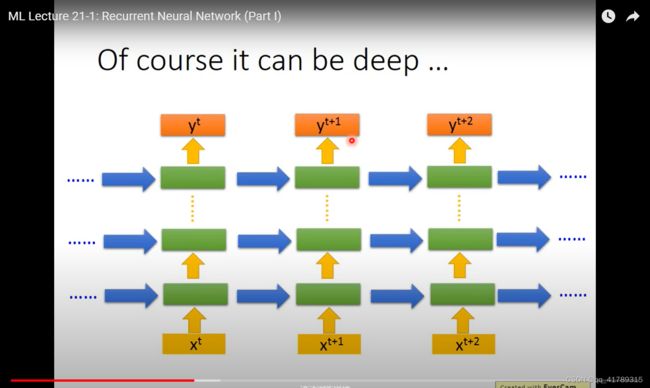
RNN分类：
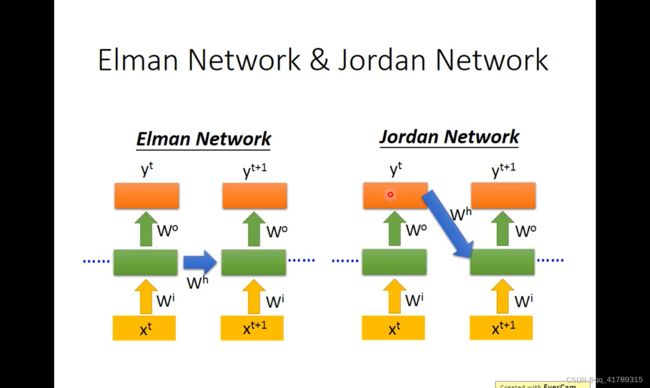
Elman Network ：将隐藏单元的输出作为下一次预测的输入
Jordan Network：将上一次的预测输出作为下一次预测的输入
    由于中间隐藏层输出结果相对来是不可控，最后的输出结果更有意义，相对来说我们知道memory存的是什么信息，所以 Jordan Network比Elman Network性能更好.

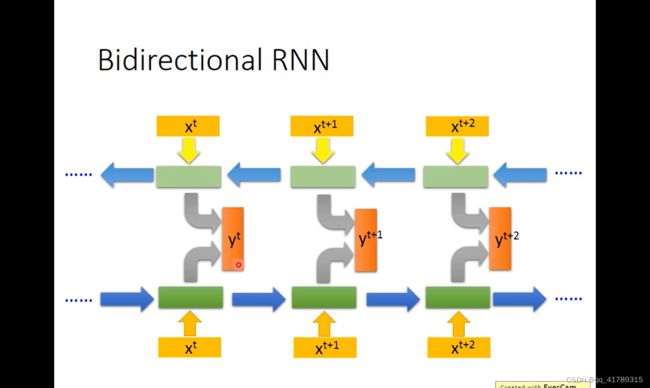
    双向RNN（Bidirectional RNN):
    RNN可以从正向和反向读取信息，可以先处理$x^t$,也可以先处理$x^{t+2}$,BiRNN输出中间结果$y^{t+1}$时,已经考虑前后两个范围,考虑的信息更多.

2 Long Short-term Memeory （LSTM）

比较长的短期记忆
3个门 4输入 1输出

2.1 LSTM 基本组成

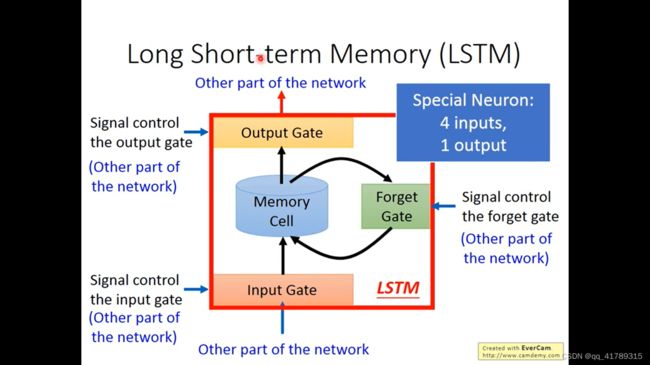
LSTM：一个单元中，有4个输入和1个输出，4个输出=3个控制信号和1个输入

组成成分：

• Input Gate：控制input数据输入
• Forget Gate：控制是否保存中间结果
• Output Gate：控制output数据输出
  
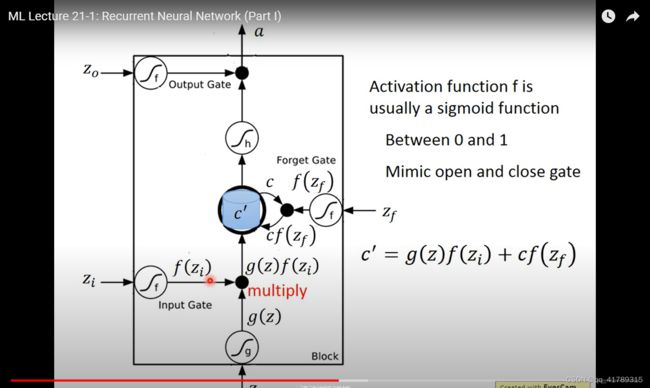
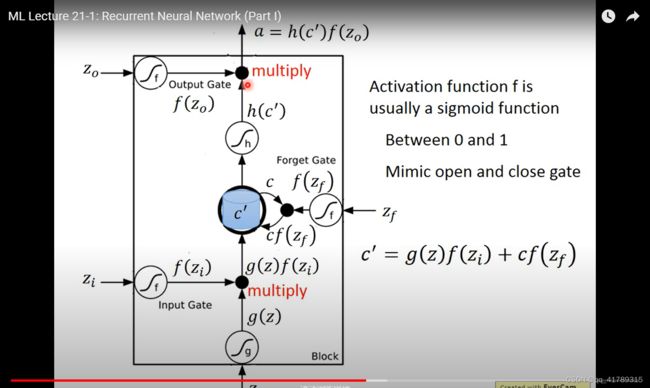
  输入：
  \qquad $z_o$：输出门控制信号
  \qquad $z_i$：输入门控制信号
  \qquad $z_f$：遗忘门控制信号
  \qquad $z$：输入
  输出：
  \qquad $a$：输出
  \qquad $f$：激活函数基本都是$sigmoid$函数，
  \qquad    值域在$0$和$1$之间，函数值决定所控制门的开关程度。值越大，门打开程度越大。
  \qquad $c$：当前隐藏层输出值
  \qquad $c^{\prime }$：下一次隐藏层输出值
  $$c^{\prime }=g(z)f(z_i)+cf(z_f)$$
  \qquad \qquad 当$f(z_i)=0$时，不考虑输入$g(z)$
  \qquad \qquad 当$f(z_i)=1$时，$g(z)$全部考虑
  \qquad \qquad 当$f(z_f)=0$时，不考虑上一次的隐藏值$c$
  \qquad \qquad 当$f(z_f)=1$时，$c$全部考虑
  
  综合所有的成分计算输出：
  $$a=h(c^{\prime })f(z_o)$$
  \qquad \qquad 当$f(z_o)=0$时，无法输出，输出的是$0$
  \qquad \qquad 当$f(z_o)=1$时，$h(c^{\prime })$全部输出
  

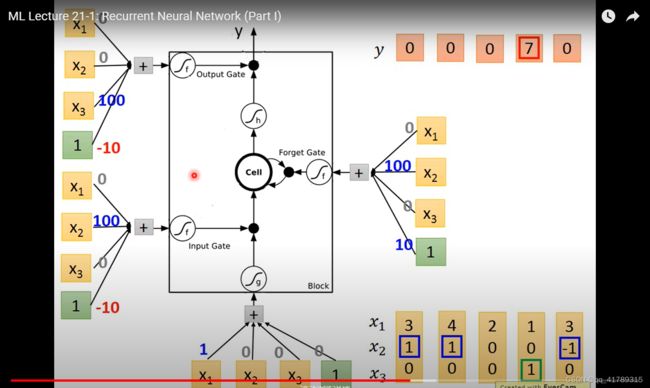
2.2 LSTM实例

\qquad 输入：2维
\qquad 输出：1维
\qquad 控制门信号：
$$\{\begin{array}{ll}{x}_2=1& x_2的值存入memory\\ x_2=-1& 重置memory\\ x_3=1& 输出memory的值\end{array}$$

\qquad 以第一个输入为例$\left[\begin{array}{c}3\\ 1\\ 0\end{array}\right]$,LSTM中一共4个输入,$\left[\begin{array}{c}3\\ 1\\ 0\end{array}\right]$分别乘以4个不同的权重和加上不同的偏差.
\qquad 得到最后的输出$y=0$,这些参数是训练得到的.

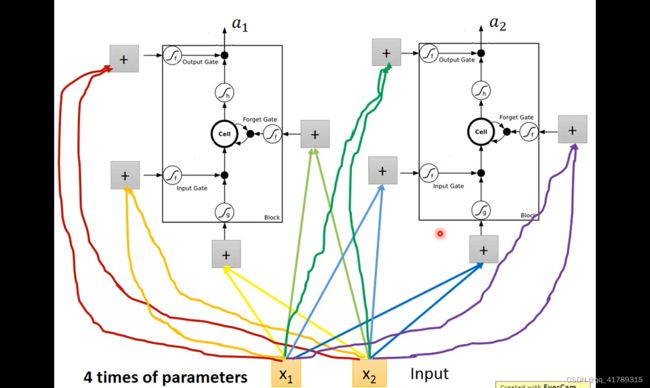
2.3LSTM 结构

\qquad 原始神经网络和LSTM网络联系
\qquad 原始神经网络结构如图：

\qquad LSTM结构：用LSTM代替神经网络的神经元;
\qquad \qquad \qquad  输入乘以4组参数，作为输入进行计算.

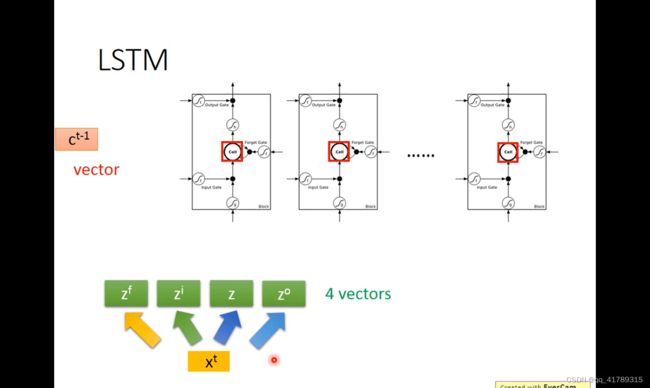
\qquad LSTM 详细结构
\qquad \qquad 输入:$x_t$
\qquad \qquad \qquad $x_t$分别乘以4个矩阵得到$z^f$，$z$，$z^i$，$z^o$ 4个输入向量
\qquad \qquad \qquad $z^f$：遗忘门控制信号向量
\qquad \qquad \qquad $z$：输入向量
\qquad \qquad \qquad $z^i$：输入门控制信号向量
\qquad \qquad \qquad $z^o$：输出们控制信号向量
\qquad \qquad 4个向量进入相应的输入口，进行计算，将向量的每一个维度的值放入LSTM的每一个单元。

取一个维度作为例,计算过程如下：
$$c^t=c^{t-1}f(z^f)+g(z)f(z^i)$$$$y^t=f(z^o)h(c^t)$$$$h^t=y^t$$

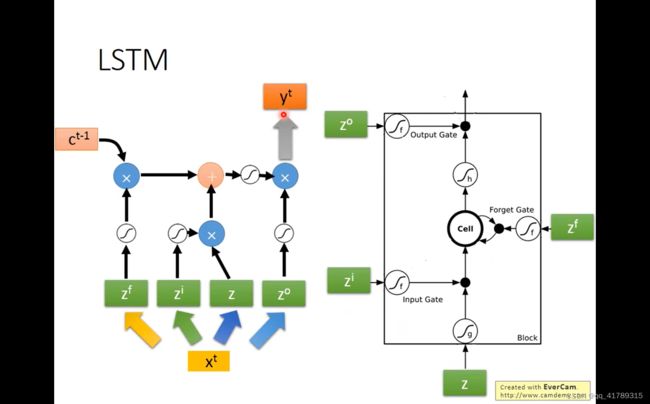
LSTM最终形态
将$c^t$，$h^t$和$x^{t+1}$作为下一次的输入

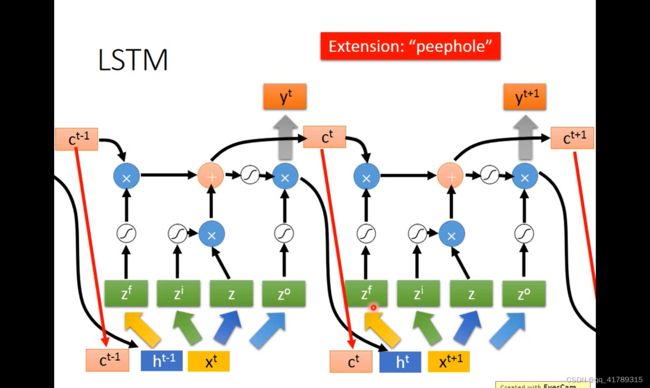
并且设计多层LSTM

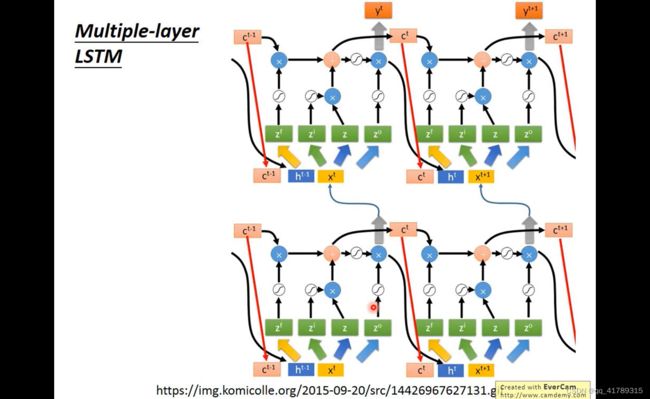
3 RNN应用

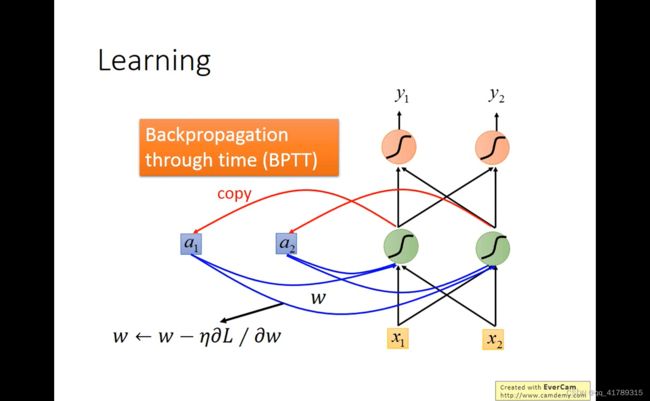
\qquad 学习目标：令$y^1$与相应的向量越相似，交叉熵损失越小

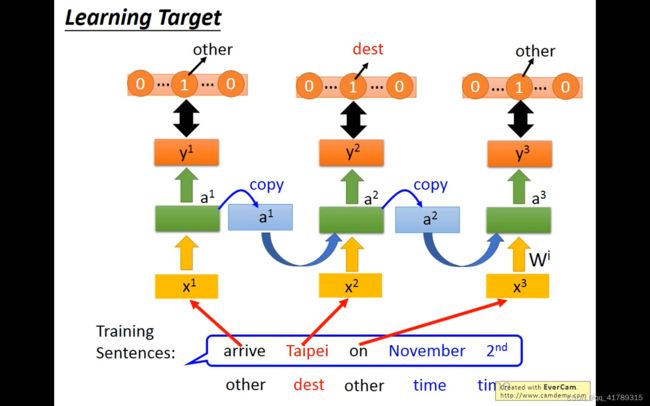
\qquad 训练:
\qquad \qquad RNN通过BPTT训练，根据梯度下降更新参数

3.1 RNN局限

RNN训练困难
原因：RNN的total loss函数有的地方非常平坦 有的地方陡峭
解决：Clipping 梯度大于某个值就等于这个值

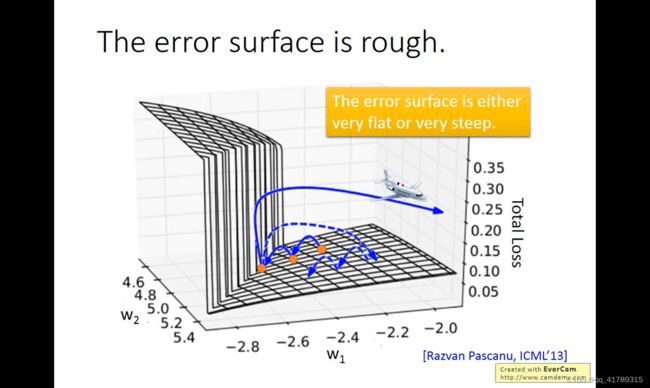
为什么损失函数会出现这种情况?
原因：同样$w$在不同的时间点反复地使用
实例：$w$在很小的范围内,$w$的梯度会很大或很小

LSTM可以解决梯度消失的问题：
原因：Memory cell 和input是相加的关系，除非遗忘门关闭否则对memory的影响不会消失，换句话说遗忘门如果开着，则不会产生梯度消失的问题。如果遗忘门关着才会把memory存储的数据清洗掉，消除原来数据的影响.

3.2 应用

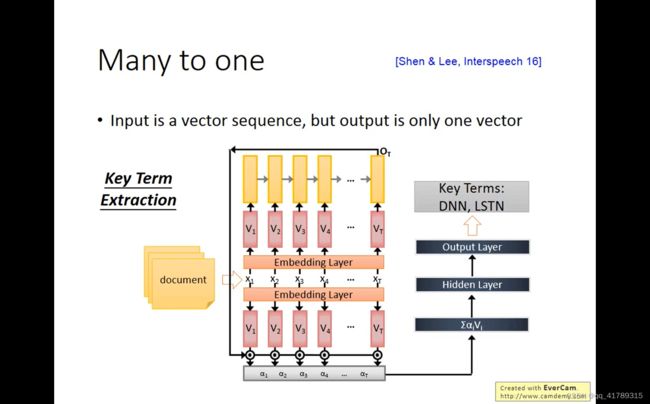
多对一：情绪分析Sentiment Analysis
通过阅读一篇文章，判断文章内容表达的情绪是正面或者负面

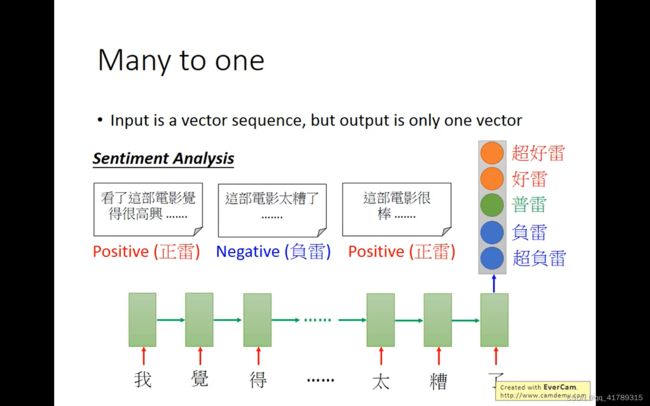
输入向量序列 输出一个向量

多对多：序列对序列 input长 output短 语音识别

CTC：解决叠字问题

CTC训练问题:

Seq2Seq 不同长度 机器翻译 训练不知道何时停止

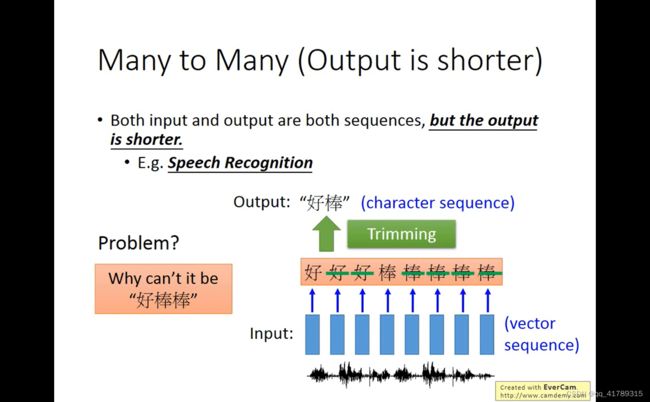
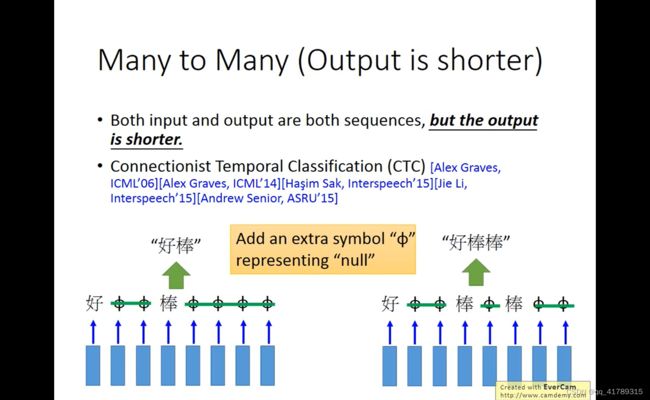
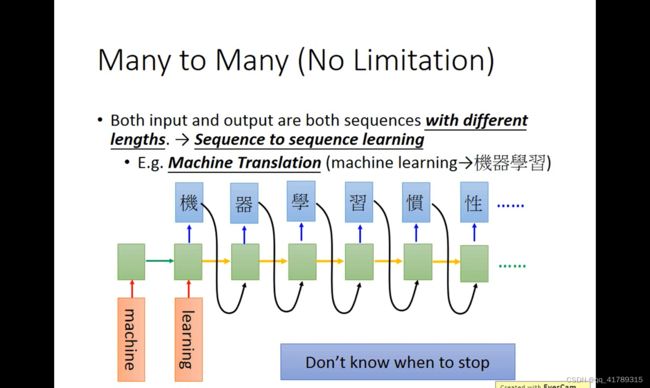
添加一个“断” ,作为停止的标志.

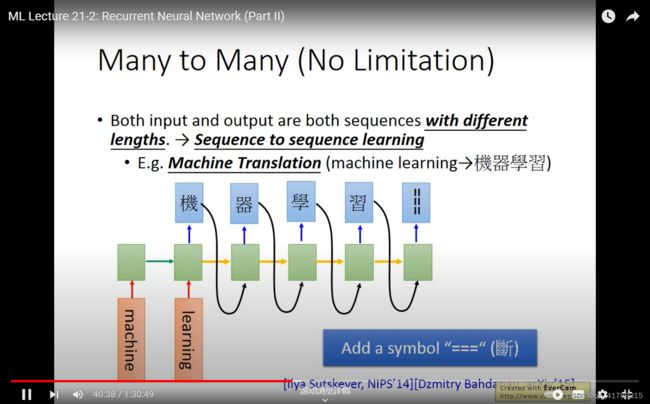
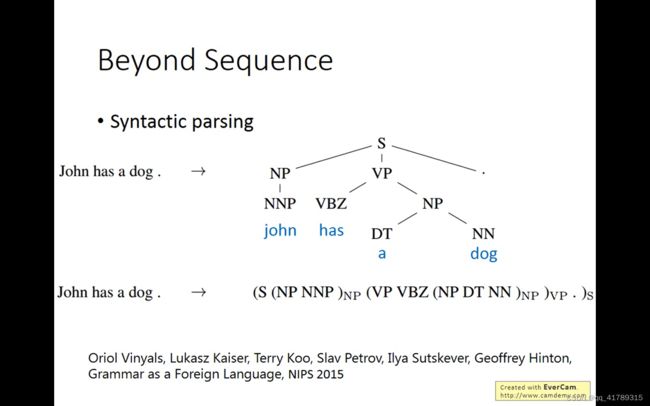
超越序列
语法分析：得到文法的结构树

Seq2Seq Auto-encoder-Text
理解单词序列含义不能忽略单词之间的顺序

Seq2Seq Auto-encoder-Speech

语音->向量

RNN encoder和decoder 联合训练joinly train
训练目标 :输出和输入越来越接近.