高斯混合模型GMM及EM迭代求解算法（含代码实现）

高斯混合模型GMM及EM迭代求解算法（含代码实现）

高斯分布与高斯混合模型

高斯分布

高斯分布大家都很熟悉了，下面是一元高斯分布的概率密度函数（Probability Density Function，PDF）：
$$P(x)=N(\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{(x-\mu {)}^2}{2{\sigma }^2})$$
其中 $\mu$ 和 ${\sigma }^2$ 分别是该高斯分布的均值和方差，而如果是多元高斯分布，则为：
$$P(x)=\frac{1}{(2\pi {)}^{\frac{D}{2}}|\Sigma {|}^{\frac{1}{2}}}\exp (-\frac{(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}{2})$$
其中 $\mu$ 、$\Sigma$ 和 $D$ 分别是均值、协方差矩阵和数据维度。

高斯混合模型

高斯混合模型，顾名思义，就是由多个单高斯模型组合而成的模型。具体来说，它是具有如下形式的概率分布模型：
$$P(x|\theta )=\sum _{k=1}^K{\alpha }_k\varphi (x|{\theta }_k)$$
其中：

• $K$ 是该混合模型中单高斯模型的个数
• ${\alpha }_k$ 是各个单高斯模型的权重系数，它满足：${\alpha }_k\ge 0$ 且 ${\sum }_{k=1}^K{\alpha }_k=1$
• $\varphi (x|{\theta }_k)$ 是第 $k$ 个单高斯模型的概率密度，也称为 $k$ 个分模型
• ${\theta }_k$ 表示第 $k$ 个单高斯模型的参数（均值和方差），即 ${\theta }_k=({\mu }_k,{\sigma }_k^2)$

为什么是高斯？

对于一般地混合模型，我们可以选用任何自己认为合适的单概率分布模型。这

里使用高斯混合模型是因为由中心极限定理可以得知，将现实世界中的数据分布假设为高斯分布是比较合理的，并且高斯分布具备很好的数学性质以及良好的计算性能。

为什么要混合？

现实世界中，我们的样本通常都是会有多个特征来描述，此时如果使用单个高斯模型来对问题进行建模，显然表达能力是不足的。而如果我们使用多个高斯模型，按照一定的权重参数将它们组合，将大大提高整个模型的表达能力。

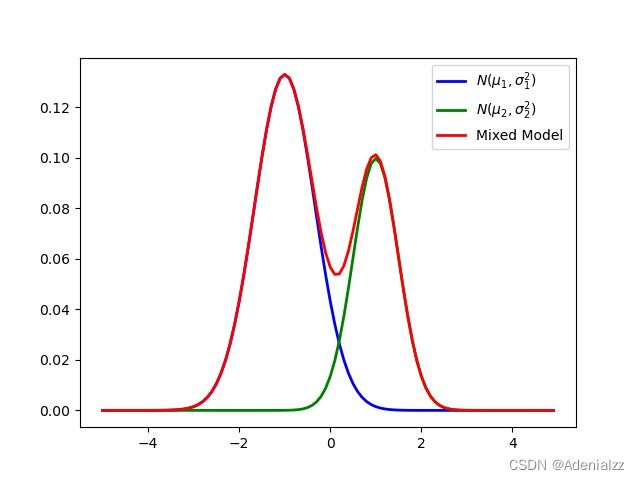
具体来说，我们知道单个高斯模型是单峰的（如图所示），即只有某一个区间的概率特别高，两端都是逐渐降低的。而如果我们使用两个高斯模型混合，得到的模型表达能力更强，可以处理现实世界中的复杂分布。

理论上，混合高斯模型的概率密度函数曲线可以是任意形状的非线性函数。

图1：单高斯模型与混合高斯模型的概率密度函数

高斯混合模型的三种理解角度

几何角度

从几何的角度来看高斯混合模型，在图像上（如图1所示），它由多个高斯分布叠加而成，是多个高斯分布的加权平均值。
$$P(x|\theta )=\sum _{k=1}^K{\alpha }_k\varphi (x|{\theta }_k)$$
在这个角度下，这里的 ${\alpha }_k$ 就是每个单高斯模型的权重。

混合模型的角度

高斯混合模型中有两个变量：

• $X=(x_1,x_2,\dots ,x_N)$：观测数据
• $Z=(z_1,z_2,\dots ,z_N)$：隐变量

这两个变量合称为完全数据。

关于什么是隐变量，这是笔者从网络上找到的一个例子，感觉这个例子和 GMM 中的引入的隐变量意思非常接近（可结合下面样本生成的角度来理解），并且比较直观：

举个例子吧

一个人拿着n个袋子，里面有m种颜色不同的球。现在这个人随机地抓球，规则如下：

1. 先随机挑一个袋子

2. 从这个袋子中随机挑一个球

如果你站在这个人旁边，你目睹了整个过程：这个人选了哪个袋子、抓出来的球是什么颜色的。然后你把每次选择的袋子和抓出来的球的颜色都记录下来（样本观察值），那个人不停地抓，你不停地记。最终你就可以通过你的记录，推测出每个袋子里每种球颜色的大致比例。并且你记录的越多，推测的就越准（中心极限定理）。

然而，抓球的人觉得这样很不爽，于是决定不告诉你他从哪个袋子里抓的球，只告诉你抓出来的球的颜色是什么。这时候，“选袋子”的过程由于你看不见，其实就相当于是一个隐变量。

隐变量在很多地方都是能够出现的。现在我们经常说的隐变量主要强调它的“latent”。所以广义上的隐变量主要就是指“不能被直接观察到，但是对系统的状态和能观察到的输出存在影响的一种东西”。

在 GMM 中， $Z$ 就是我们引入一个隐变量： $z_i,i=[1,2,\dots ,N]$ ，用它来表示对应的观测样本 $x_i$ 是属于哪一个高斯分布，具体来说，是样本 $x_i$ 属于每一个高斯分布的概率（类似软分类的思想）。

这样，很自然地，$Z$ 应当是一个离散随机变量，并服从多项分布。其分布律为：

$Z$	$C_1$	$C_2$	$\dots$	$C_K$
$P(z)$	$p_1$	$p_2$	$\dots$	$p_K$

其中 $C_k$ 表示第 $k$ 个单高斯模型， ${\sum }_{k=1}^K{p}_k=1$ 。

现在我们推导在混合模型的角度下，高斯混合模型的概率分布：
$$\begin{array}{rl}P(X)& ={\int }_{z}P(X,Z)dz\\ & =\sum _{Z}P(X,Z=C_k)\\ & =\sum _{k=1}^{K}P(Z=C_k)P(X|Z=C_k)\\ & =\sum _{k=1}^K{p}_{k}N(X|{\mu }_k,{\sigma }_k^2)\\ & =\sum _{k=1}^K{p}_k\varphi (x|{\theta }_k)\end{array}$$

推导过程解释：由联合概率密度函数 $P(X,Z)$ 求边缘概率密度函数 $P(X)$，最直接的想法就是将另一个随机变量 $Z$ 直接积掉，又由于这里的 $Z$ 是一个离散的随机变量，因此应该是积分应该写为求和，然后由公式 $P(X,Y)=P(Y)P(X|Y)$ 进行分解，此时前一项 $P(Z=C_k)$ 由分布律知就是 $p_k$ ，而后一项条件概率 $P(X|Z=C_k)$ 表示的是在选定第 $k$ 个高斯分布之后的概率密度函数，那自然就是其本身的概率密度函数 $N(X|{\mu }_k,{\sigma }_k^2)$。

这里的 $p_k$ 表示的是多项分布 $Z$ 的概率取值，这里的 $p_k$ 其实对应的就是上一种角度中的权重系数 ${\alpha }_k$ ，但是在两种不同的理解角度中有不同的物理含义。

从混合模型的角度来看，GMM是由离散的多项分布+连续的高斯分布组成。

样本生成的角度

GMM 是一个生成模型，从样本生成的角度来说：

对于每一个样本点 $x_i$ ，我们可以认为它是通过这样的过程得到的 ：先通过一个多项（$K$ 项）分布选择一个单高斯模型（相当于掷一个有 $K$ 个面的骰子），然后从对应的高斯分布中进行采样得到 $x_i$。

为什么MLE无法求出高斯混合模型的解析解

高斯混合模型的参数

高斯混合模型中的参数，就是我们公式中的 $\theta$ ，是哪些呢？很明显的，参数包括每个单高斯模型对应的权重系数 ${\alpha }_k$ 和每个单高斯模型自身的均值方差 ${\theta }_k=({\mu }_k,{\sigma }_k^2)$ 。

即混合高斯模型中的参数：
$$\theta =({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_K;{\theta }_1,{\theta }_2,\dots ,{\theta }_K)=({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_K;{\mu }_1,{\mu }_2,\dots ,{\mu }_K;{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_K)$$
观测数据 $x_1,x_2,\dots ,x_n$ 由参数为 $\theta$ 的高斯混合模型生成，

高斯混合模型的MLE尝试

对于单高斯模型，我们可以直接用极大似然估计 MLE 来求解。下面我们对混合高斯模型也进行类似的尝试，看能不能行得通：
$$\begin{array}{rl}{\hat{\theta }}_{MLE}& =\arg \underset{\theta }{\max }P(X)\\ & =\arg \underset{\theta }{\max }\log P(X)\\ & =\arg \underset{\theta }{\max }\log P(x_1)P(x_2)\dots P(X_N)=\arg \underset{\theta }{\max }\log \prod _{i=1}^{N}P(x_i)\\ & =\arg \underset{\theta }{\max }\sum _{i=1}^N\log P(x_i)\\ & =\arg \underset{\theta }{\max }\sum _{i=1}^N\log \sum _{k=1}^K{p}_k\varphi (x|{\theta }_k)\end{array}$$
至此，下一步应该是对 ${\theta }_k$ 各个值进行求偏导，然后令导数为 0。

但是我们发现，在对数 $\log$ 里面还有一个连加符号。对于对数里的连乘，我们可以利用对数的性质，直接拿出来，变为连加，但是对于对数里本身的连加符号，是非常难处理的。因此，到这一步之后，无法直接求出混合高斯模型的解析解。

接下来，我们将介绍如何利用 EM 算法来迭代求解高斯混合模型的参数 $\theta$ 。

EM算法迭代求解高斯混合模型

EM算法的一般步骤

EM 算法是一种非监督期望最大化算法。其结合了极大似然和迭代求解的方法去预估数据的分布。EM 算法主要用来解决含有隐变量的混合模型的参数估计，非常适合求解高斯混合模型。

这里直接给出一般的算法步骤，详情见：[TODO]

EM 算法通过迭代求 $L(\theta )=\log P(X|\theta )$ 的极大似然估计，每次迭代包含两部：E步，求期望；M步，求极大化。

算法流程：

• 输入：观测变量数据 $X$，隐变量数据 $Z$，联合分布 $P(X,Z|\theta )$ ，条件分布：$P(Z|X,\theta )$ ；

• 输出：模型参数 $\theta$ ；

• 步骤

  1. 选择参数的初值 ${\theta }^0$ ，开始迭代；

  2. E 步：记 ${\theta }^t$ 为第 $t$ 次迭代参数 $\theta$ 的估计值，在第 $i+1$ 次迭代的 E 步，计算：
     $$\begin{array}{rl}Q(\theta ,{\theta }^t)& ={\mathbb{E}}_Z[\log P(X,Z|\theta )|X,{\theta }^{(t)}]\\ & =\sum _Z\log P(X,Z|\theta )P(Z|X,{\theta }^{(t)})\end{array}$$
     这里 $P(Z|X,{\theta }^{(t)})$ 为给定观测数据 $X$ 和当前参数估计 ${\theta }^{(t)}$ 下隐变量数据 $Z$ 的条件概率分布；

  3. M 步：求使 $Q(\theta ,{\theta }^{(t)})$ 极大化的 $\theta$ ，确定第 $t+1$ 次迭代的参数估计值 ${\theta }^{t+1}$ :
     $${\theta }^{(t+1)}=\arg \underset{\theta }{\max }Q(\theta ,{\theta }^t)$$

  4. 重复 2、3 两步，直到收敛。

函数 $Q(\theta ,{\theta }^{(t)})$ 是 EM 算法的核心，称为 $Q$ 函数。

使用EM算法求解GMM推导

1 写出完全数据的对数似然函数

这里隐变量的定义与之前不同，是因为

回忆我们之前介绍的生成模型的角度，观测数据 $x_i,i=1,2,\dots ,N$ 是这样产生的：首先根据概率 ${\alpha }_k$ 选择第 $k$ 个单高斯分布模型 $\varphi (x|{\theta }_k)$ ，然后根据 $\varphi (x|{\theta }_k)$ 生成观测数据 $x_i$ 。注意，观测数据 $x_i$ 是已知的；反映观测数据 $x_i$ 来自第 $k$ 个单高斯模型的的数据是未知的，用隐变量 $z_{ik}$ 表示，其定义如下：
$$\begin{gathered} z_{ik}=\{\begin{array}{l}1,第i个观测来自第k个分模型\\ 0,否则\end{array} \\ i=1,2,\dots ,N;k=1,2,\dots ,K \end{gathered}$$
隐变量 $z_{ik}$ 与观测数据 $X$ 共同组成了完全数据，记为 $(x_i,z_{i1},z_{i2},\dots ,z_{iK}),i=1,2,\dots ,N$ 。

记 GMM 模型：
$$P(x|\theta )=\sum _{k=1}^K{\alpha }_k\varphi (x|{\theta }_k)$$

则有完全数据的似然函数：
$$\begin{array}{rl}P(x,z|\theta )& =\prod _{i=1}^{N}P(x_i,z_{i1},z_{i2},\dots ,z_{iK}|\theta )\\ & =\prod _{k=1}^K\prod _{i=1}^N[{\alpha }_k\varphi (x_i|{\theta }_k){]}^{z_{ik}}\\ & =\prod _{k=1}^K{\alpha }_k^{n_k}\prod _{i=1}^N[\varphi (x_i|{\theta }_k){]}^{z_{ik}}\\ & =\prod _{k=1}^K{\alpha }_k^{n_k}\prod _{i=1}^N[\frac{1}{\sqrt{2\pi }{\sigma }_k}\exp (-\frac{(x_i-{\mu }_k{)}^2}{2{\sigma }_k^2}){]}^{z_{ik}}\end{array}$$
其中，$n_l={\sum }_{i=1}^N{z}_{ik}$ ，${\sum }_{k=1}^K{n}_k=N$。

那么，完全数据的对输入似然函数为：
$$\log P(x,z|\theta )=\sum _{k=1}^K\{(n_k\log {\alpha }_k+\sum _{j=1}^N{z}_{ik}[\log (\frac{1}{\sqrt{2\pi }})-\log {\sigma }_k-\frac{1}{2{\sigma }_l^2}(x_i-{\mu }_k{)}^2]\}$$

2 E步，求期望，写出 $Q$ 函数

$$\begin{array}{rl}Q(\theta ,{\theta }^{(t)}& =\mathbb{E}(\log P(x,z|\theta )|x,{\theta }^{(t)})\\ & =\mathbb{E}\{\sum _{k=1}^K\{(n_k\log {\alpha }_k+\sum _{j=1}^N{z}_{ik}[\log (\frac{1}{\sqrt{2\pi }})-\log {\sigma }_k-\frac{1}{2{\sigma }_l^2}(x_i-{\mu }_k{)}^2]\}\}\\ & =\sum _{k=1}^K\{\sum _{i=1}^N(\mathbb{E}{z}_{ik})\log {\alpha }_k+\sum _{i=1}^N(\mathbb{E}{z}_{ik}[\log \frac{1}{\sqrt{2\pi }}-\log {\sigma }_k-\frac{1}{2{\sigma }_k^2})(x_i-{\mu }_k{)}^2]\}\end{array}$$

这里需要计算 $\mathbb{E}(z_{ik}|x,\theta )$，记为 ${\hat{z}}_{ik}$：
$$\begin{array}{rl}{\hat{z}}_{ik}& =\mathbb{E}(z_{ik}|x,\theta )=P(z_{ik}=1|x,\theta )\\ & =\frac{P(z_{ik}=1,x_i|\theta )}{{\sum }_{k=1}^{K}P(z_{ik}=1,x_i|\theta )}\\ & =\frac{P(x_i|z_{ik}=1,\theta )P(z_{ik}=1|\theta )}{{\sum }_{k=1}^{K}P(x_i|z_{ik}=1,\theta )P(z_{ik}=1,\theta )}\\ & =\frac{{\alpha }_k\varphi (x_i|{\theta }_k)}{{\sum }_{k=1}^K{\alpha }_k\varphi (x_i|{\theta }_k)},i=1,2,\dots ,N;k=1,2,\dots ,K\end{array}$$
${\hat{z}}_{ik}$ 是当前模型参数下第 $i$ 个观测数据来自第 $k$ 个模型的概率，称为分模型 $k$ 对观测数据 $x_i$ 的响应程度。

将 ${\hat{z}}_{ik}=\mathbb{E}{z}_{ik}$ 和 $n_k={\sum }_{i=1}^N\mathbb{E}{z}_{ik}$ 代入得：
$$Q(\theta ,{\theta }^{(t)})=\sum _{k=1}^K\{\sum _{i=1}^N(n_k\log {\alpha }_k+\sum _{i=1}^N({\hat{z}}_{ik}[\log \frac{1}{\sqrt{2\pi }}-\log {\sigma }_k-\frac{1}{2{\sigma }_k^2})(x_i-{\mu }_k{)}^2]\}$$

3 M步，求极大

M 步是求函数 $Q(\theta ,{\theta }^{(t)})$ 取得极大值时的 $\theta$ ，作为 ${\theta }^{(t+1)}$ ：
$${\theta }^{(t+1)}=\arg \underset{\theta }{\max }Q(\theta ,{\theta }^{(t)})$$
我们之前介绍过，GMM 模型要估计的参数为：
$$\theta =({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_K;{\theta }_1,{\theta }_2,\dots ,{\theta }_K)=({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_K;{\mu }_1,{\mu }_2,\dots ,{\mu }_K;{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_K)$$
对于 ${\mu }_k$ 和 ${\sigma }_k^2$ ，我们只需根据上式分别对他们求偏导并令其为 0 即可；

而对于 ${\hat{\alpha }}_k$ ，还需要注意约束条件 ${\sum }_{k=1}^K{\alpha }_k=1$ 。

结果如下：
$$\begin{gathered} {\hat{\mu }}_k=\frac{{\sum }_{i=1}^N{\hat{z}}_{ik}{x}_i}{{\sum }_{i=1}^N{\hat{z}}_{ik}} \\ {\hat{\sigma }}_k^2=\frac{{\sum }_{i=1}^N{\hat{z}}_{ik}(x_i-{\mu }_k{)}^2}{{\sum }_{i=1}^N{\hat{z}}_{ik}} \\ {\hat{\alpha }}_k=\frac{n_k}{N}=\frac{{\sum }_{i=1}^N{\hat{z}}_{ik}}{N} \end{gathered}$$
重复上述 2、3 步，直到收敛。

GMM模型的EM算法步骤

至此，可以给出GMM模型的EM算法步骤：

1. 选择参数的初值 ${\theta }^0$ ，开始迭代；

2. E 步：记 ${\theta }^t$ 为第 $t$ 次迭代参数 $\theta$ 的估计值，在第 $i+1$ 次迭代的 E 步，计算：
   $$Q(\theta ,{\theta }^{(t)})=\sum _{k=1}^K\{\sum _{i=1}^N(n_k\log {\alpha }_k+\sum _{i=1}^N({\hat{z}}_{ik}[\log \frac{1}{\sqrt{2\pi }}-\log {\sigma }_k-\frac{1}{2{\sigma }_k^2})(x_i-{\mu }_k{)}^2]\}$$
   这里 $P(Z|X,{\theta }^{(t)})$ 为给定观测数据 $X$ 和当前参数估计 ${\theta }^{(t)}$ 下隐变量数据 $Z$ 的条件概率分布；

3. M 步：求使 $Q(\theta ,{\theta }^{(t)})$ 极大化的 $\theta$ ，确定第 $t+1$ 次迭代的参数估计值 ${\theta }^{t+1}$ :
   $$\begin{gathered} {\hat{\mu }}_k=\frac{{\sum }_{i=1}^N{\hat{z}}_{ik}{x}_i}{{\sum }_{i=1}^N{\hat{z}}_{ik}} \\ {\hat{\sigma }}_k^2=\frac{{\sum }_{i=1}^N{\hat{z}}_{ik}(x_i-{\mu }_k{)}^2}{{\sum }_{i=1}^N{\hat{z}}_{ik}} \\ {\hat{\alpha }}_k=\frac{n_k}{N}=\frac{{\sum }_{i=1}^N{\hat{z}}_{ik}}{N} \end{gathered}$$

4. 重复 2、3 两步，直到收敛。

代码

给出参考实现[代码][[https://github.com/wl-lei/upload/blob/master/homework/GMM.py]

import numpy as np
import random

def calc_prob(X, K, pMu, pSigma):
    N = X.shape[0]
    D = X.shape[1]
    Px = np.zeros((N, K))
    for i in range(K):
        Xshift = X-np.tile(pMu[i], (N, 1))
        lambda_flag = np.e**(-5)
        conv = pSigma[i]+lambda_flag*np.eye(D)
        inv_pSigma = np.linalg.inv(conv)
        tmp = np.sum(np.dot(Xshift, inv_pSigma)*Xshift, axis=1)
        coef = (2*np.pi)**(-D/2)*np.sqrt(np.linalg.det(inv_pSigma))
        Px[:, i] = coef*np.e**(-1/2*tmp)
    return Px


def gmm(X, K):       #用array来处理
    threshold = np.e**(-15)
    N = X.shape[0]
    D = X.shape[1]
    rndp = random.sample(np.arange(N).tolist(),K)
    centroids = X[rndp,:]
    pMu = centroids
    pPi = np.zeros((1, K))
    pSigma = np.zeros((K, D, D))
    dist = np.tile(np.sum(X*X, axis=1).reshape(N,1), (1, K))+np.tile(np.sum(pMu*pMu, axis=1), (N, 1))-2*np.dot(X, pMu.T)
    labels = np.argmin(dist,axis=1)
    for i in range(K):
        index = labels == i
        Xk = X[index,:]
        pPi[:,i] = (Xk.shape[0])/N
        pSigma[i] = np.cov(Xk.T)
    Loss = -float("inf")
    while True:
        Px = calc_prob(X, K, pMu, pSigma)
        pGamma = Px*np.tile(pPi, (N, 1))
        pGamma = pGamma/np.tile(np.sum(pGamma, axis=1).reshape(N,1), (1, K))
        Nk = np.sum(pGamma, axis=0)
        pMu = np.dot(np.dot(np.diag(1/Nk), pGamma.T), X)
        pPi = Nk/N
        for i in range(K):
            Xshift = X-np.tile(pMu[i], (N, 1))
            pSigma[i] = np.dot(Xshift.T, np.dot(np.diag(pGamma[:, i]), Xshift))/Nk[i]
        L = np.sum(np.log(np.dot(Px, pPi.T)), axis=0)
        if L-Loss < threshold:
            break
        Loss = L
    return Px,pMu,pSigma,pPi
        

if __name__ == "__main__":        
    Data_list = []
    with open("data.txt", 'r') as file:
        for line in file.readlines():  
            point = []  
            point.append(float(line.split()[0]))  
            point.append(float(line.split()[1]))  
            Data_list.append(point)  
    Data = np.array(Data_list)
    Px,pMu,pSigma,pPi = gmm(Data, 2)
    print(Px,pMu,pSigma,pPi)

Ref

1. 高斯混合模型（GMM）
2. 高斯混合模型白板推导
3. 隐变量是什么
4. 详解EM算法与混合高斯模型(Gaussian mixture model, GMM)
5. 高斯混合模型(GMM)的两种详解及简化