机器学习-白板推导系列(十一)-高斯混合模型GMM(Gaussian Mixture Model)
11. 高斯混合模型GMM(Gaussian Mixture Model)
11.1 模型介绍
这一章将进入到Guassian Mixture Model (GMM)的学习。而为什么要学习GMM呢?本节从几何角度、混合模型角度和样本生成过程角度来介绍GMM。
-
几何角度
从几何角度来看:GMM为加权平均(多个高斯分布叠加而成)。以一维数据为例,我们可以看到下图通过将多个单一的高斯模型加权叠加到一起就可以获得一个高斯混合模型,这个混合模型显然具备比单个高斯模型更强的拟合能力:

一个混合高斯分布就是多个高斯分布叠加而成的。那么,概率密度函数,可以被我们写成:
p ( x ) = ∑ k = 1 K α k N ( μ k , Σ k ) , ∑ k = 1 K α k = 1. (11.1.1) p(x) = \sum_{k=1}^K \alpha_k \mathcal{N}(\mu_k, \Sigma_k), \qquad \sum_{k=1}^K \alpha_k = 1.\tag{11.1.1} p(x)=k=1∑KαkN(μk,Σk),k=1∑Kαk=1.(11.1.1) -
混合模型角度
如果当输入变量的维度高于一维时,就不能使用简单的加权来看了。因为,这时已经无法简单的用加权平均来计算了,正如下图所示:
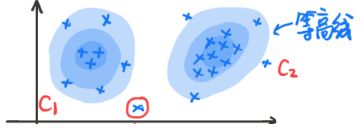
其中, X \color{blue}X X是 O b s e r v a b l e V a r i a b l e \color{blue}Observable\;Variable ObservableVariable, Z \color{blue}Z Z是 L a t e n t V a r i a b l e \color{blue}Latent\;Variable LatentVariable。这个 Z Z Z是个什么意思呢?我们先举一个小例子。看到图2中那个打了红圈圈的数据点。它既属于 C 1 C_1 C1的分布,并且也属于 C 2 C_2 C2的分布,我们可以写作:
{ X ∼ C 1 X ∼ C 2 (11.1.2) \left\{\begin{array}{ll} X \sim C_1 & \\ X \sim C_2\end{array}\right.\tag{11.1.2} {X∼C1X∼C2(11.1.2)
也 可以写成 X ∼ Z X \sim Z X∼Z,这时 Z Z Z就是一个离散的随机变量,它包含了 C 1 , C 2 , ⋯ , C N C_1,C_2,\cdots,C_N C1,C2,⋯,CN的概率分布, ∑ k = 1 N p k = 1 \sum_{k=1}^N p_k =1 ∑k=1Npk=1。 Z Z Z就是对应的样本 X X X是属于哪一个高斯分布的概率。可以被我们写成:Z Z Z C 1 C_1 C1 C 2 C_2 C2 … C N C_N CN P P P p 1 p_1 p1 p 2 p_2 p2 … p N p_N pN -
样本生成过程角度
假设有一个骰子,有 K K K个面,每个面都是不均匀的,假设可以控制每一个面的质量,那么这个骰子的面出现的概率会符合某个分布。有 K K K个面,就有 K K K个高斯分布。那么每次我们就投一下这个骰子,根据出现的面 K K K,选择在第 K K K个高斯分布中进行采样,生成一个样本点 x i x_i xi。即:- 首先第一步掷一下骰子来决定用哪个高斯分布去生成;
- 第二步在这个高斯分布下采样,采到一个样本就生成一个。
概率图可以被我们描述为如下形式:
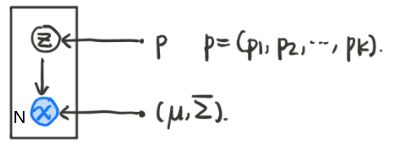
其中实心点代表模型的参数,右下角的N代表样本个数。根据一个离散的随机变量 Z Z Z来选择是选取某一个高斯分布,利用这个高斯分布 N ( μ , Σ ) \mathcal{N}(\mu,\Sigma) N(μ,Σ)来采样得到我们想要的样本点。而且,离散随机变量 Z Z Z符合一个离散分布 p = ( p 1 , p 2 , ⋯ , p k ) p = (p_1,p_2,\cdots,p_k) p=(p1,p2,⋯,pk)。
11.2 极大似然
本节试图使用极大似然估计来求解Gaussian Mixture Model (GMM)的最优参数结果。首先,明确参数的意义:
- X X X:Observed data, X = ( x 1 , x 2 , ⋯ , x N ) X = (x_1, x_2, \cdots, x_N) X=(x1,x2,⋯,xN)。
- ( X , Z ) (X,Z) (X,Z):Complete data, ( X , Z ) = { ( x 1 , z 1 ) , ( x 2 , z 2 ) , ⋯ , ( x N , z N ) } (X,Z) = \{ (x_1,z_1),(x_2,z_2),\cdots,(x_N,z_N) \} (X,Z)={(x1,z1),(x2,z2),⋯,(xN,zN)}。
- θ \theta θ:parameter, θ = { P 1 , ⋯ , P k , μ 1 , ⋯ , μ k , Σ 1 , ⋯ , Σ k } \theta=\{ P_1, \cdots, P_k, \mu_1, \cdots, \mu_k,\Sigma_1,\cdots,\Sigma_k \} θ={P1,⋯,Pk,μ1,⋯,μk,Σ1,⋯,Σk}。
- Maximum Likelihood Estimation求解参数
-
P ( x ) P(x) P(x)可以表示为:
p ( x ) = ∑ Z p ( x , Z ) = ∑ k = 1 K p ( x , z = C k ) = ∑ k = 1 K p ( z = C k ) ⋅ p ( x ∣ z = C k ) = ∑ k = 1 K p k ⋅ N ( x ∣ μ k , Σ k ) (11.2.1) \begin{aligned}p(x)&= \sum_Z p(x,Z) \\ & = \sum_{k=1}^K p(x,z = C_k) \\ & = \sum_{k=1}^K p(z = C_k)\cdot p(x|z=C_k) \\ & = \sum_{k=1}^K p_k \cdot \mathcal{N}(x|\mu_k,\Sigma_k)\end{aligned}\tag{11.2.1} p(x)=Z∑p(x,Z)=k=1∑Kp(x,z=Ck)=k=1∑Kp(z=Ck)⋅p(x∣z=Ck)=k=1∑Kpk⋅N(x∣μk,Σk)(11.2.1)
对比公式(11.1.1)可见几何角度的结果中的 α k \alpha_k αk就是混合模型中的 p k p_k pk,权重即概率。 -
尝试使用MLE求解GMM参数
尝试使用MLE求解GMM参数的解析解。实际上GMM一般使用EM算法求解, 因 为 使 用 M L E 求 导 后 , 无 法 求 出 具 体 解 析 解 \color{blue}因为使用MLE求导后,无法求出具体解析解 因为使用MLE求导后,无法求出具体解析解。所以接下来我们来看看为什么MLE无法求出解析解。
θ ^ M L E = a r g m a x θ l o g p ( X ) = a r g m a x θ l o g ∏ i = 1 N p ( x i ) = a r g m a x θ ∑ i = 1 N l o g p ( x i ) = a r g m a x θ ∑ i = 1 N l o g ∑ k = 1 K p k ⋅ N ( x i ∣ μ k , Σ k ) (11.2.2) \begin{aligned}\hat{\theta }_{MLE}&=\underset{\theta }{argmax}\; log\; p(X)\\ &=\underset{\theta }{argmax}\; log\prod_{i=1}^{N}p(x_{i})\\ &=\underset{\theta }{argmax}\sum_{i=1}^{N}log\; p(x_{i})\\ &=\underset{\theta }{argmax}\sum_{i=1}^{N}{\color{Red}{log\sum _{k=1}^{K}}}p_{k}\cdot N(x_{i}|\mu _{k},\Sigma _{k})\end{aligned}\tag{11.2.2} θ^MLE=θargmaxlogp(X)=θargmaxlogi=1∏Np(xi)=θargmaxi=1∑Nlogp(xi)=θargmaxi=1∑Nlogk=1∑Kpk⋅N(xi∣μk,Σk)(11.2.2)
想要求的 θ \theta θ包括, θ = { p 1 , ⋯ , p K , μ 1 , ⋯ , μ K , Σ 1 , ⋯ , Σ K } \color{blue}\theta=\{ p_1, \cdots, p_K, \mu_1, \cdots, \mu_K,\Sigma_1,\cdots,\Sigma_K \} θ={p1,⋯,pK,μ1,⋯,μK,Σ1,⋯,ΣK}。
-
- MLE的问题
按照之前的思路,是对每个参数进行求偏导来计算最终的结果。但 log \log log函数里是一个求和的形式,而不是求积的形式。这意味着计算非常的困难。甚至根本就求不出解析解。如果是单一的Gaussian Distribution:
log p ( x i ) = log 1 2 π σ exp { − ( x i − μ ) 2 2 σ } . (11.2.3) \log p(x_i) = \log \frac{1}{\sqrt{2 \pi} \sigma} \exp\left\{ -\frac{(x_i - \mu)^2}{2\sigma} \right\}.\tag{11.2.3} logp(xi)=log2πσ1exp{−2σ(xi−μ)2}.(11.2.3)
根据 log \log log函数优秀的性质,这个问题是可以解的。但是,很不幸 公 式 ( 11.2.2 ) 后 面 是 一 个 求 和 的 形 式 \color{red}公式(11.2.2)后面是一个求和的形式 公式(11.2.2)后面是一个求和的形式。所以,直接使用MLE求解GMM,无法得到解析解。对于含有隐变量的模型来说使用EM算法是更为合适的。
11.3 EM求解-E-Step
上一小节使用极大似然估计的方法,根本就求不出最优参数 θ \theta θ的解析解。所以本节使用迭代的方法来求近似解。EM算法的表达式,可以被我们写为:
θ ( t + 1 ) = arg max θ E z ∼ P ( z ∣ x , θ ( t ) ) [ log P ( x , z ∣ θ ) ] ⏟ Q ( θ , θ ( t ) ) . (11.3.1) \theta^{(t+1)} = \arg\max_\theta \underbrace{\mathbb{E}_{z\sim P(z|x,\theta^{(t)})} \left[ \log P(x,z|\theta) \right]}_{Q(\theta,\theta^{(t)})}.\tag{11.3.1} θ(t+1)=argθmaxQ(θ,θ(t)) Ez∼P(z∣x,θ(t))[logP(x,z∣θ)].(11.3.1)
经过一系列的迭代,可得 { θ ( 0 ) , θ ( 1 ) , ⋯ , θ ( t ) } \{\theta^{(0)},\theta^{(1)},\cdots,\theta^{(t)}\} {θ(0),θ(1),⋯,θ(t)},迭代到一定次数后的 θ ( N ) \theta^{(N)} θ(N)就是想要得到的结果。EM算法大体上可以分成两个部分,E-step和M-step:
- E(Expectation)-step: P ( z ∣ x , θ ( t ) ) ⟶ E z ∼ P ( z ∣ x , θ ( t ) ) [ log P ( x , z ∣ θ ) ] \color{red}P(z|x,\theta^{(t)}) \longrightarrow \mathbb{E}_{z\sim P(z|x,\theta^{(t)})}\left[ \log P(x,z|\theta) \right] P(z∣x,θ(t))⟶Ez∼P(z∣x,θ(t))[logP(x,z∣θ)]
- M(Maximization)-step: θ ( t + 1 ) = arg max θ E z ∼ P ( z ∣ x , θ ( t ) ) [ log P ( x , z ∣ θ ) ] \color{red}\theta^{(t+1)} = \arg\underset{\theta}{\max} \mathbb{E}_{z\sim P(z|x,\theta^{(t)})}\left[ \log P(x,z|\theta) \right] θ(t+1)=argθmaxEz∼P(z∣x,θ(t))[logP(x,z∣θ)]
-
准备
- Z Z Z是一个离散的随机变量,它包含了 C 1 , C 2 , ⋯ , C N C_1,C_2,\cdots,C_N C1,C2,⋯,CN的概率分布, ∑ k = 1 N P k = 1 \color{red}\sum_{k=1}^N P_k =1 ∑k=1NPk=1。 Z Z Z就是对应的样本 X X X是属于哪一个高斯分布的概率。可以被我们写成:
Z Z Z C 1 C_1 C1 C 2 C_2 C2 … C N C_N CN P P P p 1 p_1 p1 p 2 p_2 p2 … p N p_N pN - 使用EM算法需要用到联合概率 p ( x , z ) p(x,z) p(x,z)和后验 p ( z ∣ x ) p(z|x) p(z∣x),所有我们首先写出这两个概率的表示:
p ( x , z ) = p ( z ) p ( x ∣ z ) = p z ⋅ N ( x ∣ μ z , Σ z ) (11.3.2) \color{blue}p(x,z)=p(z)p(x|z)=p_{z}\cdot \mathcal{N}(x|\mu _{z},\Sigma _{z})\tag{11.3.2} p(x,z)=p(z)p(x∣z)=pz⋅N(x∣μz,Σz)(11.3.2) p ( z ∣ x ) = p ( x , z ) p ( x ) = p z ⋅ N ( x ∣ μ z , Σ z ) ∑ k = 1 K p k ⋅ N ( x ∣ μ k , Σ k ) (11.3.3) \color{blue}p(z|x)=\frac{p(x,z)}{p(x)}=\frac{p_{z}\cdot \mathcal{N}(x|\mu _{z},\Sigma _{z})}{\sum_{k=1}^{K}p_{k}\cdot \mathcal{N}(x|\mu _{k},\Sigma _{k})}\tag{11.3.3} p(z∣x)=p(x)p(x,z)=∑k=1Kpk⋅N(x∣μk,Σk)pz⋅N(x∣μz,Σz)(11.3.3)
-
E-step
Q ( θ , θ ( t ) ) = ∫ Z log P ( X , Z ∣ θ ) ⋅ P ( Z ∣ X , θ ( t ) ) d Z = ∑ Z log ∏ i = 1 N P ( x i , z i ∣ θ ) ⋅ ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) = ∑ Z ∑ i = 1 N log P ( x i , z i ∣ θ ) ⋅ ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) = ∑ Z [ log P ( x 1 , z 1 ∣ θ ) + log P ( x 2 , z 2 ∣ θ ) + ⋯ + log P ( x N , z N ∣ θ ) ] ⋅ ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) (11.3.4) \begin{aligned}Q(\theta, \theta^{(t)})&= \int_Z \log P(X,Z|\theta)\cdot P(Z|X,\theta^{(t)})dZ\\ &=\sum_Z \log \prod_{i=1}^N P(x_i,z_i|\theta)\cdot \prod_{i=1}^N P(z_i|x_i,\theta^{(t)})\\ &=\sum_Z \sum_{i=1}^N \log P(x_i,z_i|\theta)\cdot \prod_{i=1}^N P(z_i|x_i,\theta^{(t)})\\ &= \sum_Z [\log P(x_1,z_1|\theta)+\log P(x_2,z_2|\theta)+\cdots +\log P(x_N,z_N|\theta)]\cdot \prod_{i=1}^N P(z_i|x_i,\theta^{(t)}) \end{aligned}\tag{11.3.4} Q(θ,θ(t))=∫ZlogP(X,Z∣θ)⋅P(Z∣X,θ(t))dZ=Z∑logi=1∏NP(xi,zi∣θ)⋅i=1∏NP(zi∣xi,θ(t))=Z∑i=1∑NlogP(xi,zi∣θ)⋅i=1∏NP(zi∣xi,θ(t))=Z∑[logP(x1,z1∣θ)+logP(x2,z2∣θ)+⋯+logP(xN,zN∣θ)]⋅i=1∏NP(zi∣xi,θ(t))(11.3.4)拿连加中的第一项乘以后面的连乘来看:
∑ z 1 , z 2 , ⋯ , z N log P ( x 1 , z 1 ∣ θ ) ⋅ ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) = ∑ z 1 , z 2 , ⋯ , z N log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) ⋅ ∏ i = 2 N P ( z i ∣ x i , θ ( t ) ) ( 取 出 第 一 项 ) = ∑ z 1 log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) ∑ z 2 , ⋯ , z N ∏ i = 2 N P ( z i ∣ x i , θ ( t ) ) = ∑ z 1 log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) ∑ z 2 P ( z 2 ∣ x 2 , θ ( t ) ) ∑ z 3 P ( z 3 ∣ x 3 , θ ( t ) ) ⋯ ∑ z N P ( z N ∣ x N , θ ( t ) ) (11.3.5) \begin{aligned}&\underset{z_1,z_2,\cdots,z_N}{\sum}\log P(x_1,z_1|\theta)\cdot \prod_{i=1}^N P(z_i|x_i,\theta^{(t)})\\ =&\underset{z_1,z_2,\cdots,z_N}{\sum} \log P(x_1,z_1|\theta)\cdot P(z_1|x_1,\theta^{(t)})\cdot \prod_{i=2}^N P(z_i|x_i,\theta^{(t)})\color{green}{(取出第一项)}\\ =& \sum_{z_1} \log P(x_1,z_1|\theta)\cdot P(z_1|x_1,\theta^{(t)}) \underset{z_2,\cdots,z_N}{\sum}\prod_{i=2}^N P(z_i|x_i,\theta^{(t)})\\ =& \sum_{z_1} \log P(x_1,z_1|\theta)\cdot P(z_1|x_1,\theta^{(t)}) \sum_{z_2} P(z_2|x_2,\theta^{(t)})\sum_{z_3} P(z_3|x_3,\theta^{(t)}) \cdots \sum_{z_N} P(z_N|x_N,\theta^{(t)}) \end{aligned}\tag{11.3.5} ===z1,z2,⋯,zN∑logP(x1,z1∣θ)⋅i=1∏NP(zi∣xi,θ(t))z1,z2,⋯,zN∑logP(x1,z1∣θ)⋅P(z1∣x1,θ(t))⋅i=2∏NP(zi∣xi,θ(t))(取出第一项)z1∑logP(x1,z1∣θ)⋅P(z1∣x1,θ(t))z2,⋯,zN∑i=2∏NP(zi∣xi,θ(t))z1∑logP(x1,z1∣θ)⋅P(z1∣x1,θ(t))z2∑P(z2∣x2,θ(t))z3∑P(z3∣x3,θ(t))⋯zN∑P(zN∣xN,θ(t))(11.3.5)
由于 ∑ z i P ( z i ∣ x i , θ ( t ) ) = 1 \color{blue}\sum_{z_i} P(z_i|x_i,\theta^{(t)}) =1 ∑ziP(zi∣xi,θ(t))=1,因此,公式(11.3.5)可以简化为:
∑ z 1 , ⋯ , z N log P ( x 1 , z 1 ∣ θ ) ⋅ ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) d Z = ∑ z 1 log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) . (11.3.6) \color{red}\sum_{z_1,\cdots,z_N} \log P(x_1,z_1|\theta) \cdot \prod_{i=1}^N P(z_i|x_i,\theta^{(t)}) dZ = \sum_{z_1} \log P(x_1,z_1|\theta) \cdot P(z_1|x_1,\theta^{(t)}).\tag{11.3.6} z1,⋯,zN∑logP(x1,z1∣θ)⋅i=1∏NP(zi∣xi,θ(t))dZ=z1∑logP(x1,z1∣θ)⋅P(z1∣x1,θ(t)).(11.3.6)继续对 Q ( θ , θ ( t ) ) Q(\theta ,\theta ^{(t)}) Q(θ,θ(t))进行化简可以得到:
Q ( θ , θ ( t ) ) = ∑ z 1 l o g P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) + ⋯ + ∑ z i l o g P ( x i , z i ∣ θ ) ⋅ P ( z i ∣ x i , θ ( t ) ) = ∑ i = 1 N ∑ z i l o g P ( x i , z i ∣ θ ) ⋅ P ( z i ∣ x i , θ ( t ) ) = ∑ i = 1 N ∑ z i l o g [ P z i ⋅ N ( x i ∣ μ z i , Σ z i ) ] ⋅ P z i ( t ) ⋅ N ( x i ∣ μ z i ( t ) , Σ z i ( t ) ) ∑ k = 1 K P k ( t ) ⋅ N ( x i ∣ μ k ( t ) , Σ k ( t ) ) ( 公 式 ( 11.3.2 ) , ( 11.3.3 ) ) (11.3.7) \begin{aligned}Q(\theta ,\theta ^{(t)})&=\sum _{z_{1}}log\; P(x_{1},z_{1}|\theta )\cdot P(z_{1}|x_{1},\theta ^{(t)})+\cdots +\sum _{z_{i}}log\; P(x_{i},z_{i}|\theta )\cdot P(z_{i}|x_{i},\theta ^{(t)})\\ & =\sum_{i=1}^{N}\sum _{z_{i}}log\; P(x_{i},z_{i}|\theta )\cdot P(z_{i}|x_{i},\theta ^{(t)})\\ &=\sum_{i=1}^{N}\sum _{z_{i}}log\; [P_{z_{i}}\cdot \mathcal{N}(x_{i}|\mu _{z_{i}},\Sigma _{z_{i}})]\cdot \frac{P_{z_{i}}^{(t)}\cdot \mathcal{N}(x_{i}|\mu _{z_{i}}^{(t)},\Sigma _{z_{i}}^{(t)})}{\sum_{k=1}^{K}P_{k}^{(t)}\cdot \mathcal{N}(x_{i}|\mu _{k}^{(t)},\Sigma _{k}^{(t)})}\color{green}{(公式(11.3.2),(11.3.3))}\end{aligned}\tag{11.3.7} Q(θ,θ(t))=z1∑logP(x1,z1∣θ)⋅P(z1∣x1,θ(t))+⋯+zi∑logP(xi,zi∣θ)⋅P(zi∣xi,θ(t))=i=1∑Nzi∑logP(xi,zi∣θ)⋅P(zi∣xi,θ(t))=i=1∑Nzi∑log[Pzi⋅N(xi∣μzi,Σzi)]⋅∑k=1KPk(t)⋅N(xi∣μk(t),Σk(t))Pzi(t)⋅N(xi∣μzi(t),Σzi(t))(公式(11.3.2),(11.3.3))(11.3.7)
此处由 公 式 ( 11.3.3 ) \color{blue}公式(11.3.3) 公式(11.3.3)得,由于 ( P z i ( t ) ⋅ N ( x i ∣ μ z i ( t ) , Σ z i ( t ) ) ∑ k = 1 K P k ( t ) ⋅ N ( x i ∣ μ k ( t ) , Σ k ( t ) ) ) (\frac{P_{z_{i}}^{(t)}\cdot N(x_{i}|\mu _{z_{i}}^{(t)},\Sigma _{z_{i}}^{(t)})}{\sum_{k=1}^{K}P_{k}^{(t)}\cdot N(x_{i}|\mu _{k}^{(t)},\Sigma _{k}^{(t)})}) (∑k=1KPk(t)⋅N(xi∣μk(t),Σk(t))Pzi(t)⋅N(xi∣μzi(t),Σzi(t)))与 θ \theta θ无关,暂时写作 P ( z i ∣ x i , θ ( t ) ) ) P(z_{i}|x_{i},\theta ^{(t)})) P(zi∣xi,θ(t))) ,则:
Q ( θ , θ ( t ) ) = ∑ i = 1 N ∑ z i l o g [ P z i ⋅ N ( x i ∣ μ z i , Σ z i ) ] ⋅ P ( z i ∣ x i , θ ( t ) ) ( 公 式 ( 11.3.2 ) ) = ∑ z i ∑ i = 1 N l o g [ P z i ⋅ N ( x i ∣ μ z i , Σ z i ) ] ⋅ P ( z i ∣ x i , θ ( t ) ) = ∑ k = 1 K ∑ i = 1 N l o g [ P k ⋅ N ( x i ∣ μ k , Σ k ) ] ⋅ P ( z i = C k ∣ x i , θ ( t ) ) = ∑ k = 1 K ∑ i = 1 N [ l o g P k + l o g N ( x i ∣ μ k , Σ k ) ] ⋅ P ( z i = C k ∣ x i , θ ( t ) ) (11.3.8) \begin{aligned}Q(\theta ,\theta ^{(t)})&=\sum_{i=1}^{N}\sum _{z_{i}}log\; [P_{z_{i}}\cdot \mathcal{N}(x_{i}|\mu _{z_{i}},\Sigma _{z_{i}})]\cdot P(z_{i}|x_{i},\theta ^{(t)})\color{green}{(公式(11.3.2))}\\ &=\sum _{z_{i}}\sum_{i=1}^{N}log\; [P_{z_{i}}\cdot \mathcal{N}(x_{i}|\mu _{z_{i}},\Sigma _{z_{i}})]\cdot P(z_{i}|x_{i},\theta ^{(t)})\\ &=\sum_{k=1}^{K}\sum_{i=1}^{N}log\; [P_{k}\cdot \mathcal{N}(x_{i}|\mu _{k},\Sigma _{k})]\cdot P(z_{i}=C_{k}|x_{i},\theta ^{(t)})\\ &=\sum_{k=1}^{K}\sum_{i=1}^{N}[log\; P_{k }+log\; \mathcal{N}(x_{i}|\mu _{k},\Sigma _{k})]\cdot P(z_{i}=C_{k}|x_{i},\theta ^{(t)})\end{aligned}\tag{11.3.8} Q(θ,θ(t))=i=1∑Nzi∑log[Pzi⋅N(xi∣μzi,Σzi)]⋅P(zi∣xi,θ(t))(公式(11.3.2))=zi∑i=1∑Nlog[Pzi⋅N(xi∣μzi,Σzi)]⋅P(zi∣xi,θ(t))=k=1∑Ki=1∑Nlog[Pk⋅N(xi∣μk,Σk)]⋅P(zi=Ck∣xi,θ(t))=k=1∑Ki=1∑N[logPk+logN(xi∣μk,Σk)]⋅P(zi=Ck∣xi,θ(t))(11.3.8)
即:
Q ( θ , θ ( t ) ) = ∑ i = 1 N ∑ z i l o g [ P z i ⋅ N ( x i ∣ μ z i , Σ z i ) ] ⋅ P z i ( t ) ⋅ N ( x i ∣ μ z i ( t ) , Σ z i ( t ) ) ∑ k = 1 K P k ( t ) ⋅ N ( x i ∣ μ k ( t ) , Σ k ( t ) ) = ∑ k = 1 K ∑ i = 1 N [ l o g P k + l o g N ( x i ∣ μ k , Σ k ) ] ⋅ P ( z i = C k ∣ x i , θ ( t ) ) (11.3.9) \color{red}\begin{aligned}Q(\theta ,\theta ^{(t)}) &=\sum_{i=1}^{N}\sum _{z_{i}}log\; [P_{z_{i}}\cdot \mathcal{N}(x_{i}|\mu _{z_{i}},\Sigma _{z_{i}})]\cdot \frac{P_{z_{i}}^{(t)}\cdot \mathcal{N}(x_{i}|\mu _{z_{i}}^{(t)},\Sigma _{z_{i}}^{(t)})}{\sum_{k=1}^{K}P_{k}^{(t)}\cdot \mathcal{N}(x_{i}|\mu _{k}^{(t)},\Sigma _{k}^{(t)})}\\ &=\sum_{k=1}^{K}\sum_{i=1}^{N}[log\; P_{k }+log\; \mathcal{N}(x_{i}|\mu _{k},\Sigma _{k})]\cdot P(z_{i}=C_{k}|x_{i},\theta ^{(t)})\end{aligned}\tag{11.3.9} Q(θ,θ(t))=i=1∑Nzi∑log[Pzi⋅N(xi∣μzi,Σzi)]⋅∑k=1KPk(t)⋅N(xi∣μk(t),Σk(t))Pzi(t)⋅N(xi∣μzi(t),Σzi(t))=k=1∑Ki=1∑N[logPk+logN(xi∣μk,Σk)]⋅P(zi=Ck∣xi,θ(t))(11.3.9)
其中 K K K是隐变量的维度, N N N是 O b s e r v a b l e V a r i a b l e Observable\;Variable ObservableVariable的维度。
11.4 EM求解:M-Step
- EM算法的迭代公式为:
θ ( t + 1 ) = a r g m a x θ Q ( θ , θ ( t ) ) (11.4.1) \color{blue}\theta ^{(t+1)}=\underset{\theta }{argmax}\; Q(\theta ,\theta ^{(t)})\tag{11.4.1} θ(t+1)=θargmaxQ(θ,θ(t))(11.4.1)
我们需要求解的参数也就是, θ ( t + 1 ) = { P 1 ( t + 1 ) , ⋯ , P k ( t + 1 ) , μ 1 ( t + 1 ) , ⋯ , μ k ( t + 1 ) , Σ 1 ( t + 1 ) , ⋯ , Σ k ( t + 1 ) } \color{green}\theta^{(t+1)}=\{ P_1^{(t+1)}, \cdots, P_k^{(t+1)}, \mu_1^{(t+1)}, \cdots, \mu_k^{(t+1)},\Sigma_1^{(t+1)},\cdots,\Sigma_k^{(t+1)} \} θ(t+1)={P1(t+1),⋯,Pk(t+1),μ1(t+1),⋯,μk(t+1),Σ1(t+1),⋯,Σk(t+1)}。- X X X:Observed data, X = ( x 1 , x 2 , ⋯ , x N ) X = (x_1, x_2, \cdots, x_N) X=(x1,x2,⋯,xN)。
- ( X , Z ) (X,Z) (X,Z):Complete data, ( X , Z ) = { ( x 1 , z 1 ) , ( x 2 , z 2 ) , ⋯ , ( x N , z N ) } (X,Z) = \{ (x_1,z_1),(x_2,z_2),\cdots,(x_N,z_N) \} (X,Z)={(x1,z1),(x2,z2),⋯,(xN,zN)}。
- θ \theta θ:parameter, θ = { P 1 , ⋯ , P k , μ 1 , ⋯ , μ k , Σ 1 , ⋯ , Σ k } \theta=\{ P_1, \cdots, P_k, \mu_1, \cdots, \mu_k,\Sigma_1,\cdots,\Sigma_k \} θ={P1,⋯,Pk,μ1,⋯,μk,Σ1,⋯,Σk}。
- 求解 P K ( t + 1 ) P_K^{(t+1)} PK(t+1)
- 首先,我们来展示一下怎么求解 P k ( t + 1 ) P_k^{(t+1)} Pk(t+1)( P ( t + 1 ) = ( P 1 ( t + 1 ) , P 2 ( t + 1 ) , ⋯ , P K ( t + 1 ) ) T P^{(t+1)}=(P^{(t+1)}_1,P^{(t+1)}_2,\cdots,P^{(t+1)}_K)^T P(t+1)=(P1(t+1),P2(t+1),⋯,PK(t+1))T)。
- 在等式(11.3.9)中 ∑ k = 1 K ∑ i = 1 N ( log P k + log N ( x ∣ μ k , Σ k ) ) ⋅ P ( z i = C k ∣ x i , θ ( t ) ) \sum_{k=1}^K \sum_{i=1}^N \left( \log P_{k} + \log \mathcal{N}(x|\mu_{k},\Sigma_{k}) \right) \cdot P(z_i = C_k|x_i,\theta^{(t)}) ∑k=1K∑i=1N(logPk+logN(x∣μk,Σk))⋅P(zi=Ck∣xi,θ(t))中的 log N ( X ∣ μ k , Σ k ) \log \mathcal{N}(X|\mu_{k},\Sigma_{k}) logN(X∣μk,Σk)部分和 P k P_k Pk并没有什么关系,可以被直接忽略掉。所以,求解问题可以被描述为:
{ max p ∑ k = 1 K ∑ i = 1 N log P k ⋅ P ( z i = C k ∣ x i , θ ( t ) ) s . t . ∑ k = 1 K P k = 1 (11.4.2) \begin{cases} \underset{p}{\max} \displaystyle\sum_{k=1}^{K} \sum_{i=1}^N \log P_k \cdot P(z_i=C_k|x_i,\theta^{(t)})\\ s.t.\ \ \displaystyle\sum_{k=1}^K P_k=1 \end{cases}\tag{11.4.2} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧pmaxk=1∑Ki=1∑NlogPk⋅P(zi=Ck∣xi,θ(t))s.t. k=1∑KPk=1(11.4.2)
使用 拉 格 朗 日 乘 子 法 \color{blue}拉格朗日乘子法 拉格朗日乘子法:
L ( p , λ ) = ∑ k = 1 K ∑ i = 1 N log P k ⋅ P ( z i = C k ∣ x i , θ ( t ) ) + λ ( ∑ k = 1 K P k − 1 ) (11.4.3) L(p,\lambda) = \sum_{k=1}^{K} \sum_{i=1}^N \log P_k \cdot P(z_i=C_k|x_i,\theta^{(t)})+\lambda(\sum_{k=1}^K P_k-1)\tag{11.4.3} L(p,λ)=k=1∑Ki=1∑NlogPk⋅P(zi=Ck∣xi,θ(t))+λ(k=1∑KPk−1)(11.4.3)
对 p k p_k pk求导,并令其为 0 0 0:
∂ L ( P , λ ) ∂ P k = ∑ i = 1 N 1 P k ⋅ P ( Z i = C k ∣ X i , θ ( t ) ) + λ = 0 ⇒ ∑ i = 1 N P ( Z i = C k ∣ X i , θ ( t ) ) + P k λ = 0 ⟹ k = 1 , ⋯ , K ∑ i = 1 N ∑ k = 1 K P ( Z i = C k ∣ X i , θ ( t ) ) ⏟ 1 + ∑ k = 1 K P k ⏟ 1 λ = 0 ⇒ N + λ = 0 (11.4.4) \begin{aligned}\frac{\partial \mathcal{L}(P,\lambda)}{\partial P_k} = & \sum_{i=1}^N \frac{1}{P_k} \cdot P(Z_i = C_k|X_i,\theta^{(t)}) + \lambda = 0 \\ \Rightarrow & \sum_{i=1}^N P(Z_i = C_k|X_i,\theta^{(t)}) + P_k \lambda = 0 \\ \stackrel{k = 1,\cdots,K}{\Longrightarrow} & \sum_{i=1}^N\underbrace{\sum_{k=1}^K P(Z_i = C_k|X_i,\theta^{(t)})}_{1} + \underbrace{\sum_{k=1}^K P_k}_{1} \lambda = 0 \\ \Rightarrow & N+\lambda = 0\end{aligned}\tag{11.4.4} ∂Pk∂L(P,λ)=⇒⟹k=1,⋯,K⇒i=1∑NPk1⋅P(Zi=Ck∣Xi,θ(t))+λ=0i=1∑NP(Zi=Ck∣Xi,θ(t))+Pkλ=0i=1∑N1 k=1∑KP(Zi=Ck∣Xi,θ(t))+1 k=1∑KPkλ=0N+λ=0(11.4.4)
所以 λ = − N \lambda = -N λ=−N,代入公式 ∑ i = 1 N P ( z i = C k ∣ x ( i ) , θ ( t ) ) + P k ( t + 1 ) λ = 0 \sum_{i=1}^{N}P(z_{i}=C_{k}|x_{(i)},\theta ^{(t)})+P_{k}^{(t+1)}\lambda =0 ∑i=1NP(zi=Ck∣x(i),θ(t))+Pk(t+1)λ=0得:
∑ i = 1 N P ( z ( i ) = C k ∣ x i , θ ( t ) ) + P k ( t + 1 ) N = 0 ⇒ P k ( t + 1 ) = ∑ i = 1 N P ( z i = C k ∣ x i , θ ( t ) ) N (11.4.5) \sum_{i=1}^{N}P(z_{(i)}=C_{k}|x_{i},\theta ^{(t)})+P_{k}^{(t+1)}N=0\\ \Rightarrow P_{k}^{(t+1)}=\frac{\sum_{i=1}^{N}P(z_{i}=C_{k}|x_{i},\theta ^{(t)})}{N}\tag{11.4.5} i=1∑NP(z(i)=Ck∣xi,θ(t))+Pk(t+1)N=0⇒Pk(t+1)=N∑i=1NP(zi=Ck∣xi,θ(t))(11.4.5)
即:
P k ( t + 1 ) = ∑ i = 1 N P ( z i = C k ∣ x i , θ ( t ) ) N (11.4.6) \color{red}P_{k}^{(t+1)}=\frac{\sum_{i=1}^{N}P(z_{i}=C_{k}|x_{i},\theta ^{(t)})}{N}\tag{11.4.6} Pk(t+1)=N∑i=1NP(zi=Ck∣xi,θ(t))(11.4.6)
至于 θ \theta θ的其他部分,也就是关于 { μ 1 ( t + 1 ) , ⋯ , μ k ( t + 1 ) , Σ 1 ( t + 1 ) , ⋯ , Σ k ( t + 1 ) } \{ \mu_1^{(t+1)}, \cdots, \mu_k^{(t+1)},\Sigma_1^{(t+1)},\cdots,\Sigma_k^{(t+1)} \} {μ1(t+1),⋯,μk(t+1),Σ1(t+1),⋯,Σk(t+1)}的计算,使用的方法也是一样的,这个问题就留给各位了。
总结
- MLE与EM算法对比
为什么极大似然估计搞不定的问题,放在EM算法里面我们就可以搞定了呢?我们来对比一下两个方法中,需要计算极值的公式。
θ ^ M L E = a r g m a x θ l o g p ( X ) = a r g m a x θ ∑ i = 1 N l o g ∑ k = 1 K p k ⋅ N ( x i ∣ μ k , Σ k ) (11.5.1) \begin{array}{ll}\hat{\theta }_{MLE}&=\underset{\theta }{argmax}\; log\; p(X)\\ &=\underset{\theta }{argmax}\sum_{i=1}^{N}{\color{Red}{log\sum _{k=1}^{K}}}p_{k}\cdot N(x_{i}|\mu _{k},\Sigma _{k})\end{array}\tag{11.5.1} θ^MLE=θargmaxlogp(X)=θargmax∑i=1Nlog∑k=1Kpk⋅N(xi∣μk,Σk)(11.5.1)
θ ( t + 1 ) = a r g m a x θ ∑ k = 1 K ∑ i = 1 N ( log P k + log − N ( X i ∣ μ k , Σ k ) ) ⋅ P ( Z i = C k ∣ X i , θ ( t ) ) (11.5.2) \theta ^{(t+1)}=\underset{\theta }{argmax}\; \sum_{k=1}^K \sum_{i=1}^N \left( \log P_{k} + \log -\mathcal{N}(X_i|\mu_{k},\Sigma_{k}) \right) \cdot P(Z_i = C_k|X_i,\theta^{(t)})\tag{11.5.2} θ(t+1)=θargmaxk=1∑Ki=1∑N(logPk+log−N(Xi∣μk,Σk))⋅P(Zi=Ck∣Xi,θ(t))(11.5.2)- 极大似然估计一开始计算的就是 P ( X ) P(X) P(X),而EM算法中并没有出现有关 P ( X ) P(X) P(X)的计算,全程计算都是 P ( X , Z ) P(X,Z) P(X,Z)。
- 而 P ( X ) P(X) P(X)实际上就是 P ( X , Z ) P(X,Z) P(X,Z)的求和形式。
- 所以,每次单独的考虑 P ( X , Z ) P(X,Z) P(X,Z)就避免了在log函数中出现求和操作。
- EM算法对GMM的一般步骤:
- E(Expectation)-step:
Q ( θ , θ ( t ) ) = ∑ i = 1 N ∑ z i l o g [ P z i ⋅ N ( x i ∣ μ z i , Σ z i ) ] ⋅ P z i ( t ) ⋅ N ( x i ∣ μ z i ( t ) , Σ z i ( t ) ) ∑ k = 1 K P k ( t ) ⋅ N ( x i ∣ μ k ( t ) , Σ k ( t ) ) = ∑ k = 1 K ∑ i = 1 N [ l o g P k + l o g N ( x i ∣ μ k , Σ k ) ] ⋅ P ( z i = C k ∣ x i , θ ( t ) ) (11.5.3) \color{red}\begin{aligned}Q(\theta ,\theta ^{(t)}) &=\sum_{i=1}^{N}\sum _{z_{i}}log\; [P_{z_{i}}\cdot \mathcal{N}(x_{i}|\mu _{z_{i}},\Sigma _{z_{i}})]\cdot \frac{P_{z_{i}}^{(t)}\cdot \mathcal{N}(x_{i}|\mu _{z_{i}}^{(t)},\Sigma _{z_{i}}^{(t)})}{\sum_{k=1}^{K}P_{k}^{(t)}\cdot \mathcal{N}(x_{i}|\mu _{k}^{(t)},\Sigma _{k}^{(t)})}\\ &=\sum_{k=1}^{K}\sum_{i=1}^{N}[log\; P_{k }+log\; \mathcal{N}(x_{i}|\mu _{k},\Sigma _{k})]\cdot P(z_{i}=C_{k}|x_{i},\theta ^{(t)})\end{aligned}\tag{11.5.3} Q(θ,θ(t))=i=1∑Nzi∑log[Pzi⋅N(xi∣μzi,Σzi)]⋅∑k=1KPk(t)⋅N(xi∣μk(t),Σk(t))Pzi(t)⋅N(xi∣μzi(t),Σzi(t))=k=1∑Ki=1∑N[logPk+logN(xi∣μk,Σk)]⋅P(zi=Ck∣xi,θ(t))(11.5.3) - M(Maximization)-step:
P k ( t + 1 ) = ∑ i = 1 N P ( z i = C k ∣ x i , θ ( t ) ) N (11.5.4) \color{red}P_{k}^{(t+1)}=\frac{\sum_{i=1}^{N}P(z_{i}=C_{k}|x_{i},\theta ^{(t)})}{N}\tag{11.5.4} Pk(t+1)=N∑i=1NP(zi=Ck∣xi,θ(t))(11.5.4)
μ k ( t + 1 ) = ∑ i = 1 N P x i P ( z i = C k ∣ x i , θ ( t ) ) ∑ i = 1 N P ( z i = C k ∣ x i , θ ( t ) ) (11.5.5) \color{red}\mu_{k}^{(t+1)}=\frac{\sum_{i=1}^{N}P_{x_i}P(z_{i}=C_{k}|x_{i},\theta ^{(t)})}{\sum_{i=1}^{N}P(z_{i}=C_{k}|x_{i},\theta ^{(t)})}\tag{11.5.5} μk(t+1)=∑i=1NP(zi=Ck∣xi,θ(t))∑i=1NPxiP(zi=Ck∣xi,θ(t))(11.5.5)
Σ k ( t + 1 ) = ∑ i = 1 N ( P x i − μ k ) 2 P ( z i = C k ∣ x i , θ ( t ) ) ∑ i = 1 N P ( z i = C k ∣ x i , θ ( t ) ) (11.5.6) \color{red}\Sigma_{k}^{(t+1)}=\frac{\sum_{i=1}^{N}(P_{x_i}-\mu_k)^2\;P(z_{i}=C_{k}|x_{i},\theta ^{(t)})}{\sum_{i=1}^{N}P(z_{i}=C_{k}|x_{i},\theta ^{(t)})}\tag{11.5.6} Σk(t+1)=∑i=1NP(zi=Ck∣xi,θ(t))∑i=1N(Pxi−μk)2P(zi=Ck∣xi,θ(t))(11.5.6)
其中 K K K是隐变量的维度, N N N是 O b s e r v a b l e V a r i a b l e Observable\;Variable ObservableVariable的维度:
- X X X:Observed data, X = ( x 1 , x 2 , ⋯ , x N ) X = (x_1, x_2, \cdots, x_N) X=(x1,x2,⋯,xN)。
- ( X , Z ) (X,Z) (X,Z):Complete data, ( X , Z ) = { ( x 1 , z 1 ) , ( x 2 , z 2 ) , ⋯ , ( x N , z N ) } (X,Z) = \{ (x_1,z_1),(x_2,z_2),\cdots,(x_N,z_N) \} (X,Z)={(x1,z1),(x2,z2),⋯,(xN,zN)}。
- θ \theta θ:parameter, θ = { P 1 , ⋯ , P k , μ 1 , ⋯ , μ k , Σ 1 , ⋯ , Σ k } \theta=\{ P_1, \cdots, P_k, \mu_1, \cdots, \mu_k,\Sigma_1,\cdots,\Sigma_k \} θ={P1,⋯,Pk,μ1,⋯,μk,Σ1,⋯,Σk}。
- E(Expectation)-step:
GMM代码实现
- 子程序代码:
function [u,sig,t,iter] = fit_mix_gaussian( X,M )
%
% fit_mix_gaussian - fit parameters for a mixed-gaussian distribution using EM algorithm
%
% format: [u,sig,t,iter] = fit_mix_gaussian( X,M )
%
% input: X - input samples, Nx1 vector
% M - number of gaussians which are assumed to compose the distribution
%
% output: u - fitted mean for each gaussian
% sig - fitted standard deviation for each gaussian
% t - probability of each gaussian in the complete distribution
% iter- number of iterations done by the function
%
% initialize and initial guesses
N = length( X );
Z = ones(N,M) * 1/M; % indicators vector
P = zeros(N,M); % probabilities vector for each sample and each model
t = ones(1,M) * 1/M; % distribution of the gaussian models in the samples
u = linspace(min(X),max(X),M); % mean vector
sig2 = ones(1,M) * var(X) / sqrt(M); % variance vector
C = 1/sqrt(2*pi); % just a constant
Ic = ones(N,1); % - enable a row replication by the * operator
Ir = ones(1,M); % - enable a column replication by the * operator
Q = zeros(N,M); % user variable to determine when we have converged to a steady solution
thresh = 1e-3;
step = N;
last_step = inf;
iter = 0;
min_iter = 10;
% main convergence loop, assume gaussians are 1D
while ((( abs((step/last_step)-1) > thresh) & (step>(N*eps)) ) | (iter<min_iter) )
% E step
% ========
Q = Z;
P = C ./ (Ic*sqrt(sig2)) .* exp( -((X*Ir - Ic*u).^2)./(2*Ic*sig2) );
for m = 1:M
Z(:,m) = (P(:,m)*t(m))./(P*t(:));
end
% estimate convergence step size and update iteration number
prog_text = sprintf(repmat( '\b',1,(iter>0)*12+ceil(log10(iter+1)) ));
iter = iter + 1;
last_step = step * (1 + eps) + eps;
step = sum(sum(abs(Q-Z)));
fprintf( '%s%d iterations\n',prog_text,iter );
% M step
% ========
Zm = sum(Z); % sum each column
Zm(find(Zm==0)) = eps; % avoid devision by zero
u = (X')*Z ./ Zm;
sig2 = sum(((X*Ir - Ic*u).^2).*Z) ./ Zm;
t = Zm/N;
end
sig = sqrt( sig2 );
- 例子:
clc;clear all;close all;
set(0,'defaultfigurecolor','w')
x = [1*randn(100000,1)+3;3*randn(100000,1)-5];
%fitting
x = x(:); % should be column vectors !
N = length(x);
[u,sig,t,iter] = fit_mix_gaussian( x,2 );
sig = sig.^2;
%Plot
figure;
%Bar
subplot 221
plot(x(randperm(N)),'k');grid on;
xlim([0,N]);
subplot 222
numter = [-15:.2:10];
[histFreq, histXout] = hist(x, numter);
binWidth = histXout(2)-histXout(1);
bar(histXout, histFreq/binWidth/sum(histFreq)); hold on;grid on;
%Fitting plot
subplot 223
y = t(2)*1/sqrt(2*pi*sig(2))*exp(-(numter-u(2)).^2/2/sig(2));
plot(numter,y,'r','linewidth',2);grid on;
hold on;
y = t(1)*1/sqrt(2*pi*sig(1))*exp(-(numter-u(1)).^2/2/sig(1));
plot(numter,y,'g','linewidth',2);grid on;
%Fitting result
subplot 224
bar(histXout, histFreq/binWidth/sum(histFreq)); hold on;grid on;
y = t(2)*1/sqrt(2*pi*sig(2))*exp(-(numter-u(2)).^2/2/sig(2));
plot(numter,y,'r','linewidth',2);grid on;
hold on;
y = t(1)*1/sqrt(2*pi*sig(1))*exp(-(numter-u(1)).^2/2/sig(1));
plot(numter,y,'g','linewidth',2);grid on;
