决策树三种算法的剖析（id3，c4.5，cart）

决策树三种算法的剖析（id3，c4.5，cart）

决策树大家应该都听说过，说白了就是通过建树来处理分类和回归问题。
对于信息论的基本知识我就不多讲了，说实话我也不太清楚，我认为其实也没必要去了解，学到什么不懂学什么就好了。
进入正题！！！

id3

先来说一下最简单的id3算法。
首先我们需要知道一个算法他的度量函数也就是损失函数是什么？这是很重要的一个问题。
id3的损失函数叫做信息增益，信息增益=信息熵-条件熵。

其中：信息熵就是我们常见的熵函数：

条件熵：

看完这个我估计你还是一头雾水的，数学这东西，其实最好理解的就是举个例子么：

比如我们有15个样本D，输出为0或者1。其中有9个输出为1， 6个输出为0。 样本中有个特征A，取值为A1，A2和A3。在取值为A1的样本的输出中，有3个输出为1， 2个输出为0，取值为A2的样本输出中,2个输出为1,3个输出为0， 在取值为A3的样本中，4个输出为1，1个输出为0.
样本D的熵为： H(D)=−(915log2915+615log2615)=0.971
样本D在特征下的条件熵为： H(D|A)=515H(D1)+515H(D2)+515H(D3)　　　　 =−515(35log235+25log225)−515(25log225+35log235)−515(45log245+15log215)=0.888　　　　
对应的信息增益为 I(D,A)=H(D)−H(D|A)=0.083

至于id3的计算过程也比较简单。我这里有一个详细的matlab的id3可视化代码（注释很详细），有兴趣的可以去看看。
算法流程：
1、首先处理数据
2、计算最优特征值（这里会调用3，依次比较最优特征值）
3、计算信息增益
4、重复2、3过程。

id3的缺点：
a)ID3没有考虑连续特征，比如长度，密度都是连续值，无法在ID3运用。这大大限制了ID3的用途。

b)ID3采用信息增益大的特征优先建立决策树的节点。很快就被人发现，在相同条件下，取值比较多的特征比取值少的特征信息增益大。比如一个变量有2个值，各为1/2，另一个变量为3个值，各为1/3，其实他们都是完全不确定的变量，但是取3个值的比取2个值的信息增益大。如果校正这个问题呢？

c) ID3算法对于缺失值的情况没有做考虑

d) 没有考虑过拟合的问题

ID3 算法的作者昆兰基于上述不足，对ID3算法做了改进，这就是C4.5算法，也许你会问，为什么不叫ID4，ID5之类的名字呢?那是因为决策树太火爆，他的ID3一出来，别人二次创新，很快 就占了ID4， ID5，所以他另辟蹊径，取名C4.0算法，后来的进化版为C4.5算法。下面我们就来聊下C4.5算法

c4.5

首先c4.5的损失函数是在id3的基础上进行了改进的，从信息增益改进为信息增益率，这样就解决了id3中的取值多的样本值大于取值少的样本值的问题。
信息增益率=信息增益/特征熵

这里的特征熵就是对每一个特征求熵，很简单。这个链接有例子，不懂得可以看看。（https://blog.csdn.net/fuqiuai/article/details/79456971）
这里就解决了id3的第二个问题。
接下里解决第一个问题。
怎么样处理连续值呢？
c4.5是这样处理的：
C4.5的思路是将连续的特征离散化。比如m个样本的连续特征A有m个，从小到大排列为a1,a2,…,am,则C4.5取相邻两样本值的平均数，一共取得m-1个划分点，其中第i个划分点Ti表示为：Ti=ai+ai+12。对于这m-1个点，分别计算以该点作为二元分类点时的信息增益。选择信息增益最大的点作为该连续特征的二元离散分类点。比如取到的增益最大的点为at,则小于at的值为类别1，大于at的值为类别2，这样我们就做到了连续特征的离散化。要注意的是，与离散属性不同的是，如果当前节点为连续属性，则该属性后面还可以参与子节点的产生选择过程。

简而言之就是通过求一个特征的信息增益，然后取最大的信息增益的点作为分界线
接下来处理缺失值的问题：
缺失值存在两个问题：
第一，缺失值的特征分类？
第二，有缺失值怎么计算信息增益率？
第一个问题是通过将缺失的样本划分按照比例划分进入所有的样本中。比如缺失特征A的样本a之前权重为1，特征A有3个特征值A1,A2,A3。 3个特征值对应的无缺失A特征的样本个数为2,3,4.则a同时划分入A1，A2，A3。对应权重调节为2/9,3/9, 4/9。
第二，有缺失值怎么计算信息增益率？我们可以按照特征将数据分为有缺失值和没有缺失值两部分，然后用没有缺失值的信息增益率乘以权重代替有缺失值的信息增益率。权重就是样本数量比。
至于过拟合问题呢，那就是剪枝策略了。
这个剪枝策略还是比较复杂的，大家耐心点看吧。

常见的剪枝分为两类，一类就是预剪枝，一类就是后剪枝。
预剪枝就是开始就设定一个阈值，然后小于这个阈值的就进行剪枝。（显而易见，多了一个超参数）

我们c4.5采用的是后剪枝的方法。
我们设计了一个剪枝的损失函数：

C(T)为预测误差（也就是我们上面的损失函数），T是子树中叶子结点的个数，alpha是正则项。也就是相当于正则化了一下而已。
显而易见，当alpha为0的时候相当于不用剪枝，那么就是原始树，当alpha无限大的时候，就是每一个叶子都是一颗子树。

现在我们的目标就是求出上面这个剪枝损失函数中的alpha这个超参量

那么怎么求呢？
好办！我们写出剪枝后的损失函数：

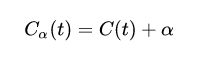
因为剪之后就只有本身一个叶子结点了，所以后面的T就等于1了。

进过公式推导可以得出alpha的值为：

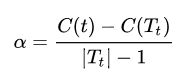
算法流程：
1、从下而上计算剪枝损失函数，更新正则化系数alpha
2、选出最大的alpha然后从上而下访问，根据最大的alpha进行剪枝。这里得到的是一个集合M
3、接下来用这个M集合交叉验证选取最优的子树T。

c4.5的缺点：
C4.5 用的是多叉树，用二叉树效率更高；（小朋友是不是有很多问题呢？？？）
C4.5 只能用于分类；
C4.5 使用的熵模型拥有大量耗时的对数运算，连续值还有排序运算；
C4.5 在构造树的过程中，对数值属性值需要按照其大小进行排序，从中选择一个分割点，所以只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时，程序无法运行。

CART

在讲CART之前有必要对前面的id3和c4.5的特点说一下。
id3和c4.5都是多叉树类型，也就是一个节点可以分出多个叉。这里有个混淆点二叉树不等于二分类！！！是不是迷茫了，看了下面的CART你就释然了。

CART的损失函数有了很大的改进，不再用信息增益系列了，用了一个与信息增益完全相反特征的损失函数-------基尼系数。
信息增益描述的是特征的混乱度，也就是信息增益越高特征越不纯净。
基尼系数刚好相反，基尼系数越大，不纯度越低！

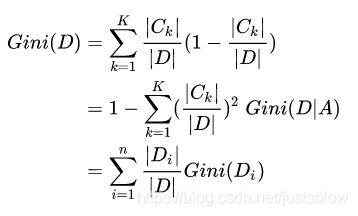
其中 k 代表类别。

基尼指数反映了从数据集中随机抽取两个样本，其类别标记不一致的概率。
此外，当 CART 为二分类，其表达式为：

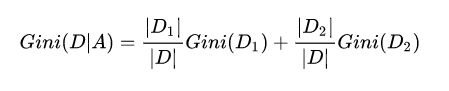
其实记住上面这个就好了，因为我们用的就是二叉树。

接下来讲一下CART对c4.5的优化：

首先是对连续特征处理的不同，把信息增益率换成基尼系数即可，另外记得把取最大改为取最小。
对离散值的处理有少许不同，假如某个特征有A,B,C三类。我们把它们进行二分类为（A,BC）(B,AC),(C,AB)。然后CART通过计算基尼系数，取最小的基尼系数的组合，然后再继续下去直至把它们全分成一类。

对于生成的决策树做预测的时候，假如测试集里的样本A落到了某个叶子节点，而节点里有多个训练样本。则对于A的类别预测采用的是这个叶子节点里概率最大的类别。

CART不光可以处理分类问题，他还可以处理回归问题。

回归：
除了概念的不同，CART回归树和CART分类树的建立和预测的区别主要有下面两点：

1)连续值的处理方法不同

2)决策树建立后做预测的方式不同。
　　　　
对于连续值的处理，我们知道CART分类树采用的是用基尼系数的大小来度量特征的各个划分点的优劣情况。这比较适合分类模型，但是对于回归模型，我们使用了常见的和方差的度量方式，CART回归树的度量目标是，对于任意划分特征A，对应的任意划分点s两边划分成的数据集D1和D2，求出使D1和D2各自集合的均方差最小，同时D1和D2的均方差之和最小所对应的特征和特征值划分点。表达式为：

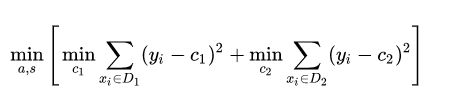
预测方式

对于决策树建立后做预测的方式，上面讲到了 CART 分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。而回归树输出不是类别，它采用的是用最终叶子的均值或者中位数来预测输出结果。

对比：

算法 支持模型 树结构 特征选择 连续值处理 缺失值处理 剪枝
ID3 分类 多叉树 信息增益 不支持 不支持 不支持
C4.5 分类 多叉树 信息增益比 支持 支持 支持
CART 分类，回归 二叉树 基尼系数，均方差 支持 支持 支持

最后来一个决策树算法小结：
终于到了最后的总结阶段了，这里我们不再纠结于ID3, C4.5和 CART，我们来看看决策树算法作为一个大类别的分类回归算法的优缺点。这部分总结于scikit-learn的英文文档。

首先我们看看决策树算法的优点：

1）简单直观，生成的决策树很直观。

2）基本不需要预处理，不需要提前归一化，处理缺失值。

3）使用决策树预测的代价是O(log2m)。 m为样本数。

4）既可以处理离散值也可以处理连续值。很多算法只是专注于离散值或者连续值。

5）可以处理多维度输出的分类问题。

6）相比于神经网络之类的黑盒分类模型，决策树在逻辑上可以得到很好的解释

7）可以交叉验证的剪枝来选择模型，从而提高泛化能力。

8） 对于异常点的容错能力好，健壮性高。

我们再看看决策树算法的缺点:

1）决策树算法非常容易过拟合，导致泛化能力不强。可以通过设置节点最少样本数量和限制决策树深度来改进。

2）决策树会因为样本发生一点点的改动，就会导致树结构的剧烈改变。这个可以通过集成学习之类的方法解决。

3）寻找最优的决策树是一个NP难的问题，我们一般是通过启发式方法，容易陷入局部最优。可以通过集成学习之类的方法来改善。

4）有些比较复杂的关系，决策树很难学习，比如异或。这个就没有办法了，一般这种关系可以换神经网络分类方法来解决。

5）如果某些特征的样本比例过大，生成决策树容易偏向于这些特征。这个可以通过调节样本权重来改善。