NNDL 作业8:RNN - 简单循环网络
NNDL 作业8:RNN - 简单循环网络
- 一、使用Numpy实现SRN
- 二、 在1的基础上,增加激活函数tanh
- 三、分别使用nn.RNNCell、nn.RNN实现SRN
-
- 1、用torch.nn.RNNCell()
- 2、nn.RNN实现:
- 五. 实现“Character-Level Language Models”源代码(必做)
- 七. “编码器-解码器”的简单实现(必做)
- 总结:
一、使用Numpy实现SRN
# coding=gbk
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t)
in_h2 = np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t)
state_t = in_h1, in_h2
print('a',state_t,in_h1,in_h2)
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')
inputs is [[1. 1.]
[1. 1.]
[2. 2.]]
state_t is [0. 0.]
--------------------------------------
inputs is [1. 1.]
state_t is [0. 0.]
a (2.0, 2.0) 2.0 2.0
output_y is 4.0 4.0
---------------
inputs is [1. 1.]
state_t is (2.0, 2.0)
a (6.0, 6.0) 6.0 6.0
output_y is 12.0 12.0
---------------
inputs is [2. 2.]
state_t is (6.0, 6.0)
a (16.0, 16.0) 16.0 16.0
output_y is 32.0 32.0
---------------
二、 在1的基础上,增加激活函数tanh
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.tanh(np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t))
in_h2 = np.tanh(np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t))
state_t = in_h1, in_h2
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')
inputs is [[1. 1.]
[1. 1.]
[2. 2.]]
state_t is [0. 0.]
--------------------------------------
inputs is [1. 1.]
state_t is [0. 0.]
output_y is 1.9280551601516338 1.9280551601516338
---------------
inputs is [1. 1.]
state_t is (0.9640275800758169, 0.9640275800758169)
output_y is 1.9984510891336251 1.9984510891336251
---------------
inputs is [2. 2.]
state_t is (0.9992255445668126, 0.9992255445668126)
output_y is 1.9999753470497836 1.9999753470497836
---------------
三、分别使用nn.RNNCell、nn.RNN实现SRN
1、用torch.nn.RNNCell()
import torch
batch_size = 1
seq_len = 3 # 序列长度
input_size = 2 # 输入序列维度
hidden_size = 2 # 隐藏层维度
output_size = 2 # 输出层维度
# RNNCell
cell = torch.nn.RNNCell(input_size=input_size, hidden_size=hidden_size)
# 初始化参数 https://zhuanlan.zhihu.com/p/342012463
for name, param in cell.named_parameters():
if name.startswith("weight"):
torch.nn.init.ones_(param)
else:
torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
seq = torch.Tensor([[[1, 1]],
[[1, 1]],
[[2, 2]]])
hidden = torch.zeros(batch_size, hidden_size)
output = torch.zeros(batch_size, output_size)
for idx, input in enumerate(seq):
print('=' * 20, idx, '=' * 20)
print('Input :', input)
print('hidden :', hidden)
hidden = cell(input, hidden)
output = liner(hidden)
print('output :', output)
==================== 0 ====================
Input : tensor([[1., 1.]])
hidden : tensor([[0., 0.]])
output : tensor([[1.9281, 1.9281]], grad_fn=<AddmmBackward0>)
==================== 1 ====================
Input : tensor([[1., 1.]])
hidden : tensor([[0.9640, 0.9640]], grad_fn=<TanhBackward0>)
output : tensor([[1.9985, 1.9985]], grad_fn=<AddmmBackward0>)
==================== 2 ====================
Input : tensor([[2., 2.]])
hidden : tensor([[0.9992, 0.9992]], grad_fn=<TanhBackward0>)
output : tensor([[2.0000, 2.0000]], grad_fn=<AddmmBackward0>)
2、nn.RNN实现:
import torch
batch_size = 1
seq_len = 3
input_size = 2
hidden_size = 2
num_layers = 1
output_size = 2
cell = torch.nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)
for name, param in cell.named_parameters(): # 初始化参数
if name.startswith("weight"):
torch.nn.init.ones_(param)
else:
torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
inputs = torch.Tensor([[[1, 1]],
[[1, 1]],
[[2, 2]]])
hidden = torch.zeros(num_layers, batch_size, hidden_size)
out, hidden = cell(inputs, hidden)
print('Input :', inputs[0])
print('hidden:', 0, 0)
print('Output:', liner(out[0]))
print('--------------------------------------')
print('Input :', inputs[1])
print('hidden:', out[0])
print('Output:', liner(out[1]))
print('--------------------------------------')
print('Input :', inputs[2])
print('hidden:', out[1])
print('Output:', liner(out[2]))
Input : tensor([[1., 1.]])
hidden: 0 0
Output: tensor([[1.9281, 1.9281]], grad_fn=<AddmmBackward0>)
--------------------------------------
Input : tensor([[1., 1.]])
hidden: tensor([[0.9640, 0.9640]], grad_fn=<SelectBackward0>)
Output: tensor([[1.9985, 1.9985]], grad_fn=<AddmmBackward0>)
--------------------------------------
Input : tensor([[2., 2.]])
hidden: tensor([[0.9992, 0.9992]], grad_fn=<SelectBackward0>)
Output: tensor([[2.0000, 2.0000]], grad_fn=<AddmmBackward0>)
五. 实现“Character-Level Language Models”源代码(必做)
import torch
# 使用RNN 有嵌入层和线性层
num_class = 4 # 4个类别
input_size = 4 # 输入维度是4
hidden_size = 8 # 隐层是8个维度
embedding_size = 10 # 嵌入到10维空间
batch_size = 1
num_layers = 2 # 两层的RNN
seq_len = 5 # 序列长度是5
# 准备数据
idx2char = ['e', 'h', 'l', 'o'] # 字典
x_data = [[1, 0, 2, 2, 3]] # hello 维度(batch,seqlen)
y_data = [3, 1, 2, 3, 2] # ohlol 维度 (batch*seqlen)
inputs = torch.LongTensor(x_data)
labels = torch.LongTensor(y_data)
# 构造模型
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.emb = torch.nn.Embedding(input_size, embedding_size)
self.rnn = torch.nn.RNN(input_size=embedding_size, hidden_size=hidden_size, num_layers=num_layers,
batch_first=True)
self.fc = torch.nn.Linear(hidden_size, num_class)
def forward(self, x):
hidden = torch.zeros(num_layers, x.size(0), hidden_size)
x = self.emb(x) # (batch,seqlen,embeddingsize)
x, _ = self.rnn(x, hidden)
x = self.fc(x)
return x.view(-1, num_class) # 转变维2维矩阵,seq*batchsize*numclass -》((seq*batchsize),numclass)
model = Model()
# 损失函数和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.05) # lr = 0.01学习的太慢
# 训练
for epoch in range(15):
optimizer.zero_grad()
outputs = model(inputs) # inputs是(seq,Batchsize,Inputsize) outputs是(seq,Batchsize,Hiddensize)
loss = criterion(outputs, labels) # labels是(seq,batchsize,1)
loss.backward()
optimizer.step()
_, idx = outputs.max(dim=1)
idx = idx.data.numpy()
print("Predicted:", ''.join([idx2char[x] for x in idx]), end='')
print(",Epoch {}/15 loss={:.3f}".format(epoch + 1, loss.item()))
C:\Users\74502\ven\Scripts\python.exe C:/Users/74502/PycharmProjects/pythonProject/drtyhyh.py
Predicted: hhhhh,Epoch 1/15 loss=1.487
Predicted: lhlll,Epoch 2/15 loss=1.161
Predicted: lhlll,Epoch 3/15 loss=0.993
Predicted: ohloo,Epoch 4/15 loss=0.849
Predicted: ohlol,Epoch 5/15 loss=0.677
Predicted: ohlol,Epoch 6/15 loss=0.502
Predicted: ohlol,Epoch 7/15 loss=0.375
Predicted: ohlol,Epoch 8/15 loss=0.281
Predicted: ohlol,Epoch 9/15 loss=0.209
Predicted: ohlol,Epoch 10/15 loss=0.153
Predicted: ohlol,Epoch 11/15 loss=0.109
Predicted: ohlol,Epoch 12/15 loss=0.077
Predicted: ohlol,Epoch 13/15 loss=0.054
Predicted: ohlol,Epoch 14/15 loss=0.040
Predicted: ohlol,Epoch 15/15 loss=0.030
进程已结束,退出代码为 0
翻译Character-Level Language Models 相关内容
The Unreasonable Effectiveness of Recurrent Neural Networks
递归神经网络(rnn)有一些神奇的东西。我仍然记得当我训练我的第一个递归网络图像字幕。在训练的几十分钟内,我的第一个婴儿模型(带有相当随意选择的超参数)开始生成非常漂亮的图像描述,这些图像看起来很有意义。有时候,你的模型的简单程度与你从模型中得到的结果的质量之比超出了你的预期,这就是其中的一次。当时让这个结果如此令人震惊的是,人们普遍认为rnn应该很难训练(随着经验的增加,我实际上得出了相反的结论)。快进大约一年:我一直在训练rnn,我已经多次见证了它们的力量和强壮,然而它们神奇的输出仍然有办法让我开心。这篇文章就是要和你分享一些这种魔力。
顺序。根据你的背景,你可能想知道:是什么让循环网络如此特别?普通神经网络(以及卷积网络)的一个明显的局限性是它们的API太受限制:它们接受固定大小的向量作为输入(例如图像),并产生固定大小的向量作为输出(例如不同类别的概率)。不仅如此:这些模型使用固定数量的计算步骤(例如,模型中的层数)来执行这种映射。递归网络更令人兴奋的核心原因是它们允许我们进行操作顺序向量:输入、输出中的序列,或者在大多数情况下两者都有。几个例子可以使这一点更加具体:

每个矩形是一个向量,箭头代表函数(如矩阵乘法)。输入向量是红色的,输出向量是蓝色的,绿色向量代表RNN状态(稍后会有更多介绍)。从左至右:(1)没有RNN的普通处理模式,从固定大小的输入到固定大小的输出(例如图像分类)。(2)序列输出(例如,图像字幕拍摄图像并输出一句话)。(3)序列输入(例如,情感分析,其中给定句子被分类为表达积极或消极情感)。(4)序列输入和序列输出(例如,机器翻译:RNN读取英语句子,然后输出法语句子)。(5)同步序列输入和输出(例如,我们希望标记视频的每一帧的视频分类)。请注意,在每种情况下,长度序列都没有预先指定的约束,因为递归转换(绿色)是固定的,可以应用任意多次。
正如您所料,与从一开始就注定要经过固定数量的计算步骤的固定网络相比,操作的顺序机制要强大得多,因此对我们这些渴望构建更智能系统的人来说也更有吸引力。此外,正如我们稍后将看到的,rnn使用固定(但已学习)的函数将输入向量与其状态向量相结合,以产生新的状态向量。用编程术语来说,这可以解释为用某些输入和一些内部变量运行一个固定的程序。从这个角度来看,rnn本质上描述了程序。事实上,众所周知rnn是图灵完备的在某种意义上,它们可以模拟任意程序(具有适当的权重)。但是类似于神经网络的通用近似定理,你不应该对此做过多解读。事实上,当我什么都没说。
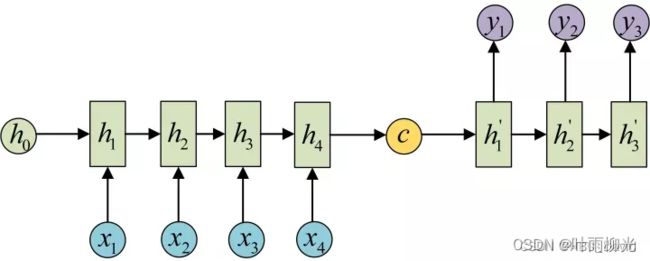
七. “编码器-解码器”的简单实现(必做)
import torch
import numpy as np
import torch.nn as nn
import torch.utils.data as Data
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
letter = [c for c in 'SE?abcdefghijklmnopqrstuvwxyz']
letter2idx = {n: i for i, n in enumerate(letter)}
seq_data = [['man', 'women'], ['black', 'white'], ['king', 'queen'], ['girl', 'boy'], ['up', 'down'], ['high', 'low']]
# Seq2Seq Parameter
n_step = max([max(len(i), len(j)) for i, j in seq_data]) # max_len(=5)
n_hidden = 128
n_class = len(letter2idx) # classfication problem
batch_size = 3
def make_data(seq_data):
enc_input_all, dec_input_all, dec_output_all = [], [], []
for seq in seq_data:
for i in range(2):
seq[i] = seq[i] + '?' * (n_step - len(seq[i])) # 'man??', 'women'
enc_input = [letter2idx[n] for n in (seq[0] + 'E')] # ['m', 'a', 'n', '?', '?', 'E']
dec_input = [letter2idx[n] for n in ('S' + seq[1])] # ['S', 'w', 'o', 'm', 'e', 'n']
dec_output = [letter2idx[n] for n in (seq[1] + 'E')] # ['w', 'o', 'm', 'e', 'n', 'E']
enc_input_all.append(np.eye(n_class)[enc_input])
dec_input_all.append(np.eye(n_class)[dec_input])
dec_output_all.append(dec_output) # not one-hot
# make tensor
return torch.Tensor(enc_input_all), torch.Tensor(dec_input_all), torch.LongTensor(dec_output_all)
enc_input_all, dec_input_all, dec_output_all = make_data(seq_data)
class TranslateDataSet(Data.Dataset):
def __init__(self, enc_input_all, dec_input_all, dec_output_all):
self.enc_input_all = enc_input_all
self.dec_input_all = dec_input_all
self.dec_output_all = dec_output_all
def __len__(self): # return dataset size
return len(self.enc_input_all)
def __getitem__(self, idx):
return self.enc_input_all[idx], self.dec_input_all[idx], self.dec_output_all[idx]
loader = Data.DataLoader(TranslateDataSet(enc_input_all, dec_input_all, dec_output_all), batch_size, True)
# Model
class Seq2Seq(nn.Module):
def __init__(self):
super(Seq2Seq, self).__init__()
self.encoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # encoder
self.decoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # decoder
self.fc = nn.Linear(n_hidden, n_class)
def forward(self, enc_input, enc_hidden, dec_input):
enc_input = enc_input.transpose(0, 1) # enc_input: [n_step+1, batch_size, n_class]
dec_input = dec_input.transpose(0, 1) # dec_input: [n_step+1, batch_size, n_class]
# h_t : [num_layers(=1) * num_directions(=1), batch_size, n_hidden]
_, h_t = self.encoder(enc_input, enc_hidden)
# outputs : [n_step+1, batch_size, num_directions(=1) * n_hidden(=128)]
outputs, _ = self.decoder(dec_input, h_t)
model = self.fc(outputs) # model : [n_step+1, batch_size, n_class]
return model
model = Seq2Seq().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
for epoch in range(5000):
for enc_input_batch, dec_input_batch, dec_output_batch in loader:
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
h_0 = torch.zeros(1, batch_size, n_hidden).to(device)
(enc_input_batch, dec_intput_batch, dec_output_batch) = (
enc_input_batch.to(device), dec_input_batch.to(device), dec_output_batch.to(device))
# enc_input_batch : [batch_size, n_step+1, n_class]
# dec_intput_batch : [batch_size, n_step+1, n_class]
# dec_output_batch : [batch_size, n_step+1], not one-hot
pred = model(enc_input_batch, h_0, dec_intput_batch)
# pred : [n_step+1, batch_size, n_class]
pred = pred.transpose(0, 1) # [batch_size, n_step+1(=6), n_class]
loss = 0
for i in range(len(dec_output_batch)):
# pred[i] : [n_step+1, n_class]
# dec_output_batch[i] : [n_step+1]
loss += criterion(pred[i], dec_output_batch[i])
if (epoch + 1) % 1000 == 0:
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Test
def translate(word):
enc_input, dec_input, _ = make_data([[word, '?' * n_step]])
enc_input, dec_input = enc_input.to(device), dec_input.to(device)
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
hidden = torch.zeros(1, 1, n_hidden).to(device)
output = model(enc_input, hidden, dec_input)
# output : [n_step+1, batch_size, n_class]
predict = output.data.max(2, keepdim=True)[1] # select n_class dimension
decoded = [letter[i] for i in predict]
translated = ''.join(decoded[:decoded.index('E')])
return translated.replace('?', '')
print('test')
print('man ->', translate('man'))
print('mans ->', translate('mans'))
print('king ->', translate('king'))
print('black ->', translate('black'))
print('up ->', translate('up'))
print('old ->', translate('old'))
print('high ->', translate('high'))
Epoch: 1000 cost = 0.002802
Epoch: 1000 cost = 0.002701
Epoch: 2000 cost = 0.000594
Epoch: 2000 cost = 0.000530
Epoch: 3000 cost = 0.000171
Epoch: 3000 cost = 0.000170
Epoch: 4000 cost = 0.000059
Epoch: 4000 cost = 0.000056
Epoch: 5000 cost = 0.000019
Epoch: 5000 cost = 0.000021
test
man -> women
mans -> women
king -> queen
black -> white
up -> down
old -> down
high -> low
进程已结束,退出代码为 0
总结:
这次主要复习了RNN、seq2seq模型,对比了nn.RNN()和nn.RNNCell()的不同,还要继续学习。