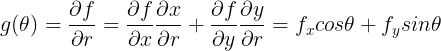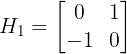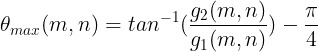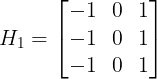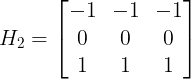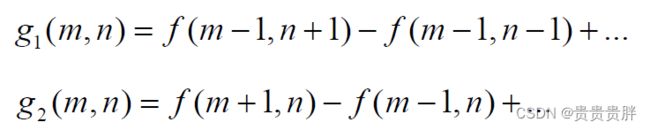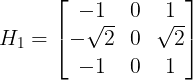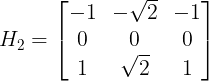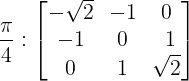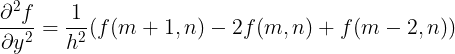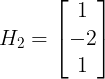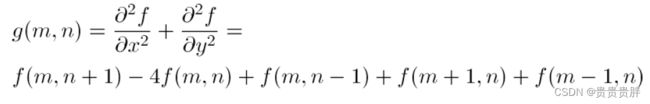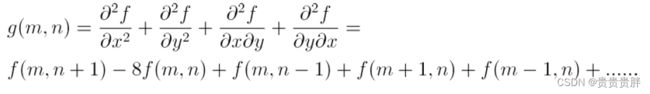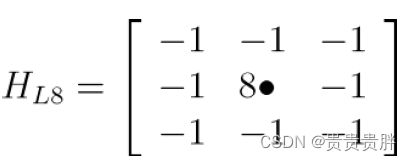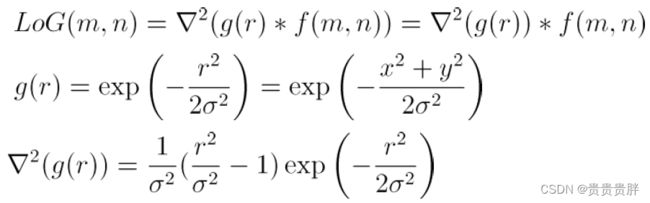第七章 图像分割

        本章主要内容为基于边缘的图像分割，包括图像点、线、边缘的分割；一阶边缘检测算子：Roberts、Prewitt、Sobel、Isotropic、Sobel、方向Sobel、Kirsch；二阶边缘检测算子LoG；过零点检测原理；Canny边缘检测。基于区域图像分割：阈值分割法；基于区域增长的分割；基于区域分裂与合并的分割。科普内容为Marr计算机视觉原理。

        本章要求重点掌握内容为图像分割的基本概念，图像点、线、边缘检测的基本原理，一阶边缘检测算子的基本原理和特点，二阶边缘检测算子的基本原理和特点，过零点检测的基本原理，阈值分割法的基本原理，区域增长的基本原理。本章科普内容为图像分割在图像分析系统中的地位，基于边缘的图像分割基本概念，基于区域的图像分割的基本概念，Marr计算机视觉原理。

7.1 图像分割引言

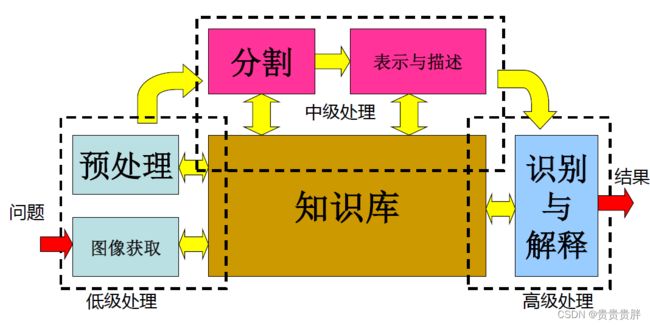
        图像分割属于图像处理当中的中级处理，图像分析系统的构成如下图所示。

         图像分割是指把图像分解成构成它的部件和对象的过程，有兴趣地定位感兴趣对象在图像中位置和范围。

        图像分割的基本策略是基于灰度值的两个基本特性：区域之间的不连续性与区域内部的相似性进行分割。

        （1）根据像素值的不连续性：先找到点、线（宽度为1）、边（不定宽度），再确定区域（边缘）。

         （2）根据像素值的相似性：通过选择阈值，找到灰度值相似的区域，区域的外轮廓就是对象的边（区域）

 7.2 基于边缘的图像分割

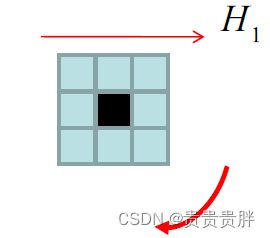
 7.2.1 点的检测

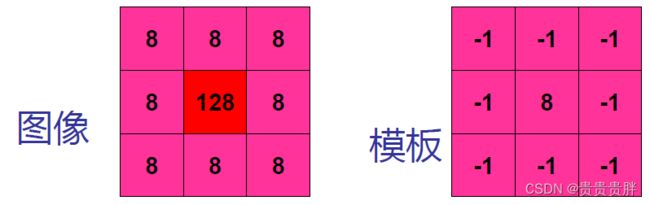
        用空域的高通滤波器来检测孤立点：

 

        设阈值T=64，R>T，则目标点为孤立点。

 7.2.2 线的检测

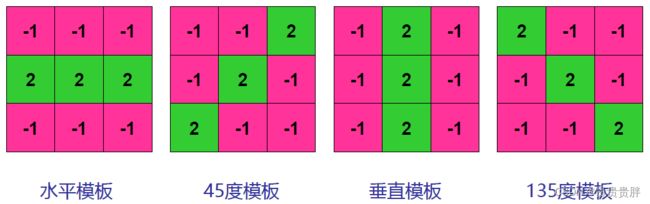
        通过比较典型模板的计算值，确定一个点是否在某个方向上的线上：

         对示例图像进行线的检测：

         用四种模板分别进行计算：

        （1）水平模板：

        （2）45度模板：

        （3）垂直模板：

        （4）135度模板：

        线的检测——算法描述：依次计算4个方向上的典型检测模板，得到Ri  (i=1,2,3,4)，如果|Ri|＞|Rj|（i≠j），那么这个点被称为在方向上更接近模板i所代表的线；

7.2.3 边的检测

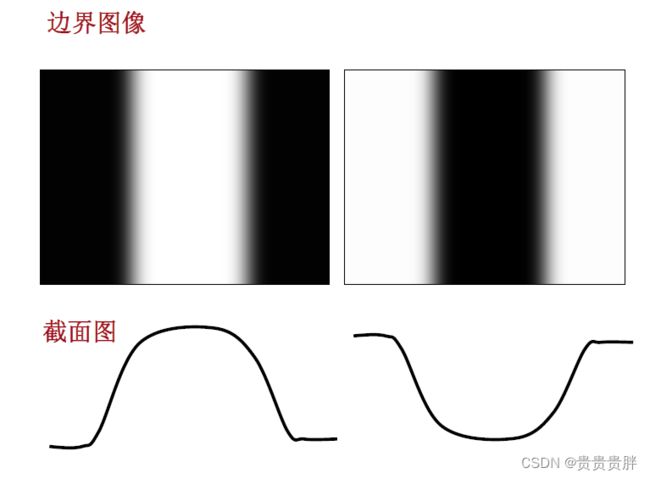
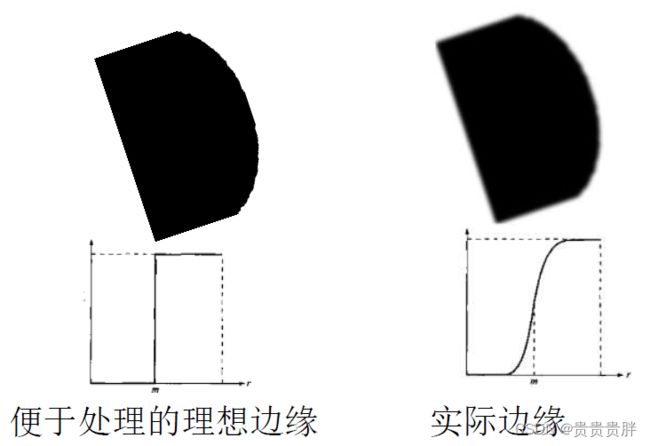
        边界的定义：是两个具有相对不同灰度值特性的区域的边界线。

        边界检测适用于：假定问题中的区域非常类似，两个区域之间的过渡，仅仅根据灰度的不连续性便可确定。

        边界检测不适用于：当假定问题中的区域没有非常类似，阈值分割技术一般来说比边缘检测更加实用。

        边缘检测的基本思想：使用计算局部微分算子来完成边的检测。

 7.2.3.1 一阶边缘检测算子

        边缘是指图像中灰度发生急剧变化的区域。是图像的一种紧描述（compact description），是图像最基本特征，包含图像中用于识别的有用信息，具有明显的视觉意义。

        目标边缘、图像纹理甚至噪声都能成为边缘。

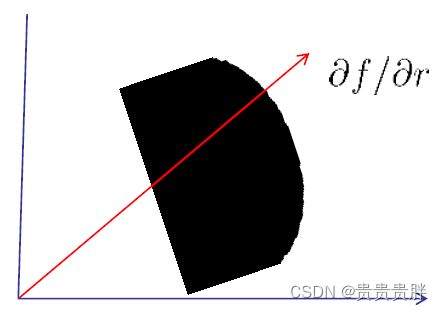
        边缘检测：求图像f中各点梯度的局部最大值和方向来确定边缘。

        方向导数：

        当  取最大值时：

        梯度方向：

        幅值：

         梯度离散化计算：

        （1）后向差分：

        （2）前向差分：

 

         

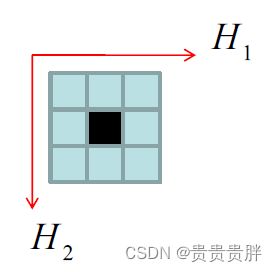
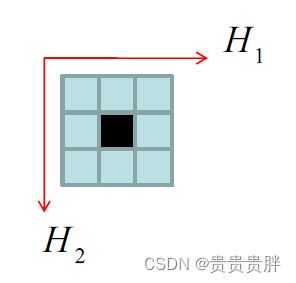
        梯度算子的推广：梯度检测实质上是在图像的两个正交方向上分别作差分运算，然后综合起来查看图像灰度变化的剧烈程度。设两个方向为H1和H2，梯度为g1(m,n), g2(m,n)，则

      

      

        梯度方向：

        幅值：

 

         

        常用一阶边缘检测算子：

        1. Roberts

                                  

 

        梯度方向：

        幅值：与梯度算子定义相同；

        特点：（讨论要点）方向、模板尺寸，定位准确程度，有无平滑因素，对噪声敏感程度。

        2.Prewitt

                                                

         梯度方向：与梯度算子定义相同；

         幅值：与梯度算子定义相同；

         特点：（讨论要点）方向，模板尺寸，定位准确程度，有无平滑因素，对噪声敏感程度。

        3. Sobel

                                          

 

         梯度方向：与梯度算子定义相同；

         幅值：与梯度算子定义相同；

         特点：（讨论要点）方向，模板尺寸，定位准确程度，有无平滑因素，对噪声敏感及抑制程度。

        4. 各向同性Sobel

                                

         梯度方向：与梯度算子定义相同；

         幅值：与梯度算子定义相同；

         特点：（讨论要点）方向，模板尺寸，定位准确程度，有无平滑因素，对噪声敏感及抑制程度, 权重影响。

        权值与邻点与中心点的距离成正比或反比，检测沿不同方向边缘时梯度幅度一致或不一致。

        5. 多方向Sobel

        检测特定方向的边缘（仍从梯度角度出发）

                          

         6. Kirsch

         Kirsch使用8个模板来确定梯度幅度值和梯度方向：

         图像中各点与8个模板逐一卷积，最大响应为输出：

         梯度方向：最大响应值对应的模板序号（量化方向）

7.2.3.2 二阶边缘检测算子

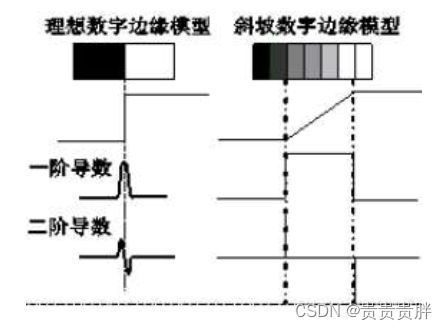
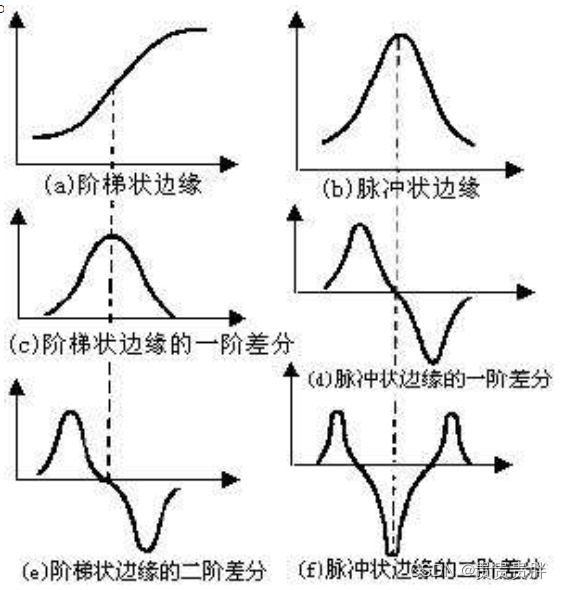
        图像的二阶微分：理论上，图像阶梯状边缘处的一阶微分（梯度）对应极值点，通过一阶导数可以确定；对于图像脉冲状边缘，一阶导数较难确定，需要借助二阶导数。

（1）图像的二阶微分离散化求解，需考虑像素距离h：

`        改为双向差分，偏移当前点：

         模板表达：

                                               

 

（2） 图像的二阶微分梯度幅值：

         该算子也称为Laplace算子，其特点是具有旋转不变性：

         模板表达：

 （3）包含交叉方向的Laplace算子：

         模板表达：

         考虑距中心点距离的模板表达：

         拉普拉斯算子缺点：（1）对噪声的敏感；（2）会产生双边效果；（3）不能检测出边的方向。

        拉普拉斯算子的应用：拉普拉斯算子不能直接用于边的检测，通常只起辅助作用；检测一个像素是在边的亮的一边还是暗的一边，利用零跨越，确定边的位置。

7.2.3.3 图像过零点检测（Marr-Hildreth算子）

        图像边缘处的二阶微分应该为零，确定过零点（Zero-Crossing）的位置要比确定极值点容易得多，也更为精确。但二阶微分对噪声更敏感，为抑制噪声，先平滑滤波然后作二次微分，通常用高斯函数作平滑滤波，因此有LoG（Laplacian of Gaussian）算子。用双高斯差函数DoG（Difference of Gaussians）对图像作卷积来近似检测边缘点（过零点）。

         过零点的检测所依赖的范围与参数有关，但边缘位置与sigma的选择无关，若只关心全局性的边缘，可选取较大范围（如sigma=4时，邻域接近40个像素宽）来获取明显的边缘。

        过零点检测更为可靠，不易受噪声影响，但缺点是对形状作了过分平滑，会丢失明显角点；还有产生环形边缘的倾向。

7.2.3.4 Canny边缘检测算法

        Canny边缘检测算法是最优的阶梯型边缘（step edge）检测算法，三个标准下，Canny边缘检测算子对受白噪声影响的阶跃型边缘最优：

        （1）检测标准：不丢失重要的边缘，不应有虚假的边缘；

        （2）定位标准：实际边缘与检测到的边缘位置之间的偏差最小；

        （3）单响应标准：将多个响应降低为单个边缘响应；

        Canny边缘检测算子是基于如下概念：边缘检测算子针对1D信号表达，对检测标准和定位标准最优；如果考虑第三个标准（多个响应），要通过数值优化得到最优解。该最优滤波器可有效地近似为标准差为σ的高斯平滑滤波器的一阶微分，误差小于20%。这与LoG边缘检测算子很相似。将边缘检测算子推广到2D情况。阶跃边缘由位置、方向和可能的幅度（强度）来确定。

        Canny边缘检测算法：

        （1）对于递增的标准差（重复（2）到（6）步骤）；

        （2）将图像f与尺度为高斯函数作卷积；

        （3）对图像中的每个像素，估计局部边缘法向量n；

        （4）用非最大抑制公式找到边缘位置；

        （5）用公式计算边缘强度：

        （6）对边缘图像作滞后阈值化处理，消除虚假响应；

        （7）用特征综合方法，收集来自多尺度的最终的边缘信息。

7.3 图像分割：基于区域的分割法

7.3.1 阈值分割法

        阈值分割法可分为：

        （1）通过交互方式得到阈值；

        （2）通过直方图得到阈值；

        （3）通过边界特性选择阈值；

        （4）简单全局分割；

        （5）分割连通区域；基于多个变量的阈值；

7.3.1.1 通过直方图取得阈值

        通过直方图得到阈值的依据：边界上的点的灰度值出现次数较少。

        通过直方图取得阈值的取值方法：取直方图谷底（最小值）的灰度值为阈值T。

        通过直方图取阈值的缺点：会受到噪声的干扰，最小值不是预期的阈值，而偏离期望的值。

        通过直方图取阈值方法的改进：1）取两个峰值之间的某个固定位置，如中间位置上。由于峰值代表的是区域内外的典型值，一般情况下，比选谷底更可靠，可排除噪声的干扰。2）对噪声的处理，对直方图进行平滑处理。

 7.3.1.2 通过边界特性选择阈值

        通过边界特性选择阈值，具有以下优点：

        （1）在前景和背景所占区域面积差别很大的时候，不会造一个灰度级的波峰过高、而另一个过低；

        （2）边缘上的点在区域内还是区域外的概率是相等的，因此可以增加波峰的对称性；

        （3）基于梯度和拉普拉斯算子的像素，可以增加波峰的高度；

        通过边界特性选择阈值，该算法的实现如下：

        （1）对图像进行梯度计算，得到梯度图像；

        （2）得到梯度值最大的那一部分（比如10%）的像素直方图；

        （3）通过直方图的谷底，得到阈值T；

        如果使用拉普拉斯算子，不通过直方图，直接得到阈值，方法是使用拉普拉斯算子过滤图像，将0跨越点对应的灰度值为阈值T。

7.3.1.3 简单全局阈值分割

        简单全局阈值分割的基本思想是用前述方法获得阈值T，并产生一个二值图，区分出前景对象和背景。

        简单全局阈值分割的算法实现如下：

        （1）规定一个阈值T，逐行扫描图像；

        （2）凡灰度级大于T的，颜色置255；凡灰度级小于T的，颜色置0；

 7.3.1.4 分割连通区域        

        分割连通区域的基本思想是用前述方法获得阈值T，并产生一个二值图，区分出单独的连通前景对象和背景区域。

        分割连通区域的算法实现如下：

        （1）规定一个阈值T，上下左右4个方向进行逐行扫描图像；

        （2）凡灰度级大于T的，颜色置255；凡灰度级小于T的，颜色置0；

7.3.1.5 基于多个变量的阈值

        基于多个变量的阈值的基本思想：把前面的方法扩展到多维空间，则寻找波谷的过程变为寻找点簇的过程。

        基于多个变量的阈值的算法实现：通过各维分量波谷之间进行逻辑与运算，从波谷重合的点，得到实际的阈值T。

7.4 图像分割：面向区域的分割

        基本概念：面向区域的分割的目标是将区域R划分为若干子区域R1、R2、···、Rn，这些子区域满足3个主要条件：

        （1）完备性：

        （2）连通性：每一个Ri都是一个连通区域；

        （3）独立性：对于任意i≠j，

        面向区域的分割的方法：

        （1）像素几何的区域增长：

                ① 根据图像的不同应用选择一个或一组种子，它或者是最亮或最暗的点，或者是位于点簇中心的点；

                ② 选择一个描述符（条件）；

                ③ 从该种子开始向外扩张，首先把种子像素加入结果集合，然后不断将与集合中各个像素连通、且满足描述符的像素加入集合；

                ④ 上一过程进行到不再有满足条件的新结点加入集合为止；

        （2）区域分裂与合并：

                ① 对图像中灰度级不同的区域，均分为四个子区域；

                ② 如果相邻子区域所有像素的灰度级相同，则将其合并；

                ③ 反复进行上两步操作，直至不再有新的分裂与合并为止；

         改进方法：根据小区域内的灰度分布的相似性进行区域合并的方法，称为统计假说检测法：

        （1）把图像分块，形成大小为n*n的小矩形区域；

        （2）比较邻接区域的灰度直方图，如果灰度分布情况相似，就合并为一个区域；

        （3）反复进行（2）的操作，直至区域合并完成为止；

        P.S 如果n过大，区域形状不自然，小的对象物体就会漏过；若n过小，可靠性就会减弱。n应设置为5~10的范围内。

7.5 Marr计算机视觉理论框架

        计算机视觉是近20~30年出现的新技术，其目标是利用场景的一幅或几幅图像来达到理解场景内容，其终极目标就是模拟一套智能系统，类似人的眼睛和大脑的功能，能对场景的内容进行有选择性的处理、主动性的识别，目的性的观察等等。

        计算机视觉的基本假设是：可以用计算的方式来模拟人类的视觉机制。

         马赫带（Mach Band）现象：一种主观的边缘对比效应。当观察两块亮度不同的区域时，边界处亮度对比加强，使轮廓表现得特别明显。

         V1视觉皮层区处理以后，目前假说认为有三条以上视觉路径分别处理运动、形状、颜色。

        Marr提出开始到现在一直是计算机视觉的基本研究理论，他主要将视觉研究从信号处理的角度进行理解，将视觉研究分为三个层次：

        （1）理论层次——计算理论计算的目的是什么？为什么它是合适的？它是依据什么决策实施的？

        （2）算法表达——计算的输入与输出采取什么表达形式？计算理论如何完成？

        （3）硬件实现——硬件实现表达与算法如何物理实现？

        Marr同时从信息处理将视觉分为三个阶段：原始信息、2.5维信息及三维信息：

        （1）初始简图（Primal Sketch）：提取出明显的轮廓和边缘信息；

        （2）2.5维简图（2.5D Sketch）：提取图像中物体在3D世界中的深度信息和其表面各处的方向信息；

        （3）以物体为中心的3维表示（3D Representation）：得到场景的三维几何信息；