常见的卷积神经网络模型

---

一、LeNet

       LeNet诞生于1994年，由深度学习三巨头之一的Yan LeCun提出，他也被称为卷积神经网络之父。
       LeNet主要用来进行手写字符的识别与分类，准确率达到了98%，并在美国的银行中投入了使用.
       LeNet莫定了现代卷积神经网络的基础。

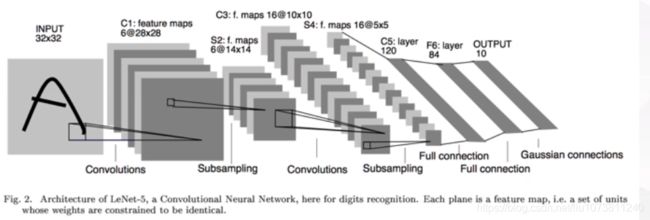
       LeNet网络除去输入输出层总共有六层网络,卷积核都是5*5的，stride=1, 池化都是平均池化:conv->pool->conv->pool->-conv(fc)->fc

二、AlexNet

AlexNet是2012年ImageNet竞赛冠军获得者Hinton和他的学生AlexKrizhevsky设计的。

2.1 AlexNet的优点

(1) 成功使用ReLU作为CNN的激活函数，并验证其效果在较深的网络超过了Sigmoid,成功解决了Sigmoid在网络较深时的梯度弥散问题。

(2) 训练时使用Dropout随机忽略一部分 神经元，以避免模型过拟合。在AlexNet中 主要是最后几个全连接层使用了Dropout。

(3) 在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化，AlexNet全 部使用最大池化，避免平均池化的模糊化效果。并且AlexNet中提出让步长比池化核的尺寸小，这样池化层的输出之间会有重叠和覆盖，提升了特征的丰富性。

(4) 提出了LRN(局部响应归一化)层，对局部神经元的活动创建竞争机制，使得其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力。

(5) 使用CUDA加速深度卷积网络的训练，利用GPU强大的并行计算能力，处理神经网络训练时大量的矩阵运算。

(6) 数据增强，随机地从256x256的原始图像中截取224x224大小的区域(以及水平翻转的镜像)，相当于增加了2*(256-224)^2=2048倍的数据量。如果没有数据增强，仅靠原始的数据量，参数众多的CNN会陷入过拟合中，使用了数据增强后可以大大减轻过拟合，提升泛化能力。

三：VGGNet

       VGGNet是牛津大学计算机视觉组和Google DeepMind公司一起研发的深度卷积神经网络，并取得了2014年lmagenet比赛定位项目第一名和分类项目第二名。vgg版本很多，常用的是VGG16，VGG19网络。

       图为VGG16的网络结构，共16层(不包括池化和softmax层)，所有的卷积核都使用3x3的大小，池化都使用大小为2x2, 步长为2的最大池化，卷积层深度依次为64 ->128-> 256-> 512 ->512.VGG-16有16个卷积层，包括五组卷积层和3个全连接层，即: 16=2+2+3+3+3+3.

3.1 VGG的特点

（1）LRN层无性能增益(A-LRN)VGG作者通过网络A-LRN发现，AlexNet曾经用到的LRN层(localresponse normalizstion,局部响应归一化)并没有带来性能的提升，因此在其它组的网络中均没再出现LRN层。

（2）随着深度增加，分类性能逐渐提高(A、B、C、D、E)从11层的A到19层的E， 网络深度增加对top1和top5的错误率下降很明显。

（3）多个小卷积核比单个大卷积核性能好(B) 。VGG作者做了实验用B和自己一个不在实验组里的较浅网络比较，较浅网络用conv5x5来代替B的两个conv3x3，结果显示多个小卷积核比单个大卷积核效果要好。

3.2 VGG与AlexNet的比较

（1） VGGNet网络层非常深，把网络层数加到了16-19层(不包括池化和softmax层)，
而AlexNet是8层结构。
（2）将卷积层提升到卷积块的概念。卷积块有2~3个卷积层构成，使网络有更大感受野的同时能降低网络参数，同时多次使用Relu激活函数有更多的线性变换，学习能力更强。
（3） 在训练时和预测时使用Multi-Scale做数据增强。训练时将同一张图片缩放到不同的尺寸，再随机剪裁到224*224的大小，能够增加数据量。预测时将同一张图片缩放到不同尺寸做预测，最后取平均值。

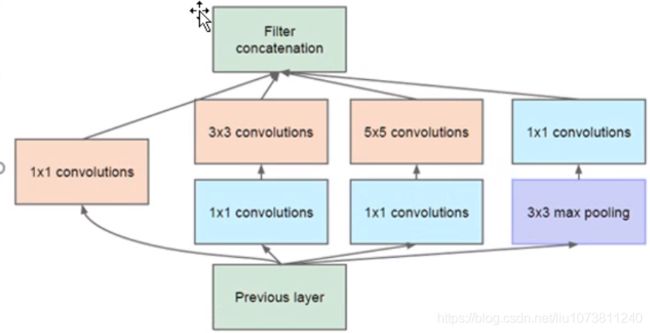
四：GoogLeNet(Google inception Net)

       Inception V1（也称为GoogLeNet，命名致敬Google和LeNet），是2014年由Christian Szegedy提出的一种全新的深度神经网络，该网络结构获得2014年ImageNet大赛的冠军。这两种网络结构都是通过增大网络的深度来获得更好的效果，但是深度的加深会带来一些副作用，比如过拟合、梯度消失、计算太复杂等，Inception提供了另外一种思路，增强卷积模块功能，可以在增加网络深度和宽度的同时减少参数。

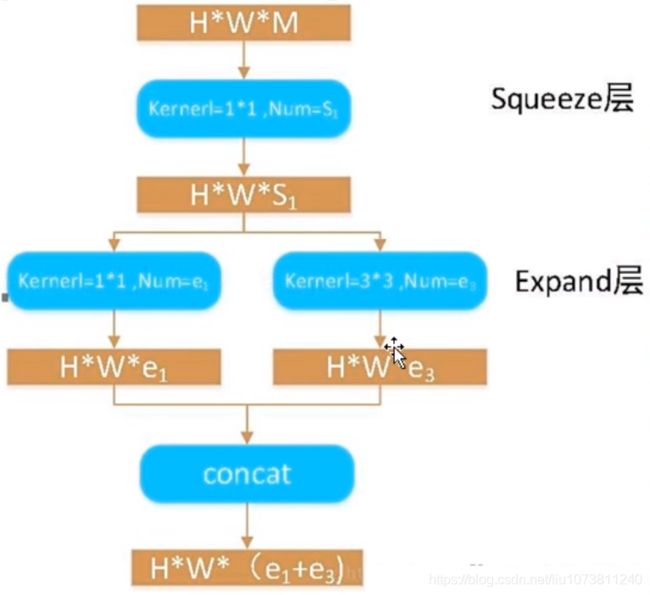
五：SqueezeNet

SqueezeNet的模型压缩使用了3个策略：

(1) 将3x3卷积替换成 1x1卷积：通过这一步，一个卷积操作的参数数量减少了9倍；

(2) 减少3x3 卷积的通道数：一个3x3卷积的计算量是 3x3xMxN（其中 M, N分别是输入Feature Map和输出Feature Map的通道数），作者认为这样一个计算量过于庞大，因此希望将 M, N减小以减少参数数量.

(3) 将下采样后置：作者认为较大的Feature Map含有更多的信息，因此将降采样往分类层移动。注意这样的操作虽然会提升网络的精度，但是它有一个非常严重的缺点：即会增加网络的计算量

五：ResNet

5.1 什么是残差？

       在统计学中，残差和误差是非常容易混淆的两个概念。误差是衡量观测值和真实值之间的差距，残差是指预测值和观测值之间的差距。对于残差网络的命名原因，作者给出的解释是，网络的一层通常可以看做y=F(x), 而残差网络的一个残差块可以表示为 H(x)=F(x) + x，也就是F(x)=H(x)-x ，在单位映射中， y=x 便是观测值，而 H(X) 是预测值，所以 F(X)便对应着残差，因此叫做残差网络。

5.2 残差网络背后的原理

       如果没有残差，没有这些捷径或者跳跃连接，凭经验你会发现随着网络深度的加深，训练错误会先减少，然后增多。而理论上，随着网络深度的加深，应该训练得越来越好才对。也就是说，理论上网络深度越深好。但实际上，如果没有残差网络，对于一个普通网络来说，深度越深意味着用优化算法越难训练。实际上，随着网络深度的加深，训练错误会越来越多。

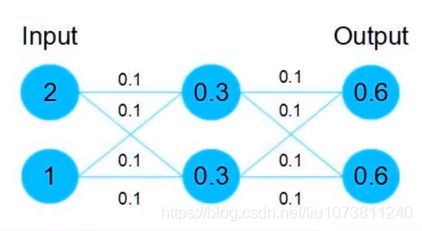
       假设该层网络只经过线性变换，没有bias也没有激活函数。我们发现因为随机初始化权重一般偏向于0，那么经过该网络的输出值为[0.6 0.6]，很明显会更接近与[0 0]，而不是[2 1]，相比与学习h(x)=x，模型要更快到学习F(x)=0。并且ReLU能够将负数激活为0，过滤了负数的线性变化，也能够更快的使得F(x)=0。

       这样当网络自己决定哪些网络层为冗余层时，使用ResNet的网络很大程度上解决了学习恒等映射的问题，用学习残差F(x)=0更新该冗余层的参数来代替学习h(x)=x更新冗余层的参数。这样当网络自行决定了哪些层为冗余层后，通过学习残差F(x)=0来让该层网络恒等映射上一层的输入，使得有了这些冗余层的网络效果与没有这些冗余层的网络效果相同，这样很大程度上解决了网络的退化问题。

5.3 ResNet能够解决的问题

（1）解决了梯度弥散问题
（2）解决了网络退化的问题
（3）适合解决各种复杂的问题

5.4 网络退化的原因

       假设已经有了一个最优化的网络结构，是18层。当我们设计网络结构的时候，我们并不知道具体多少层次的网络时最优化的网络结构，假设设计了34层网络结构。那么多出来的16层其实是冗余的，我们希望训练网络的过程中，模型能够自己训练这16层为恒等映射，也就是数据经过这些层时的输入与输出完全一样。

       但是往往模型很难将这16层恒等映射的参数学习正确，那么就一定会不比最优化的18层网络结构性能好，这就是随着网络深度增加，模型会产生退化现象。它不是由过拟合产生的，而是由冗余的网络层学习了不是恒等映射的参数造成的。

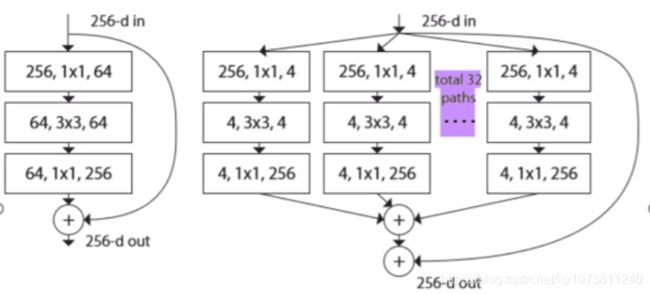
六：Deep Residual Learning

       作者的核心创新点提出了 aggregrated transformations，用一种平行堆叠相同拓扑结构的blocks代替原来 ResNet 的三层卷积的block，在不明显增加参数量级的情况下提升了模型的准确率，同时由于拓扑结构相同，超参数也减少了，便于模型移植。另外该算法目前只有Torch版本。

七：DenseNet

综合来看，DenseNet的优势主要体现在以下几个方面：

(1) 由于密集连接方式，DenseNet提升了梯度的反向传播，使得网络更容易训练。由于每层可以直达最后的误差信号，实现了隐式的“deep supervision”.

(2) 参数更小且计算更高效，这有点违反直觉，由于DenseNet是通过concat特征来实现短路连接，实现了特征重用，并且采用较小的growth rate，每个层所独有的特征图是比较小的；

(3) 由于特征复用，最后的分类器使用了低级特征。

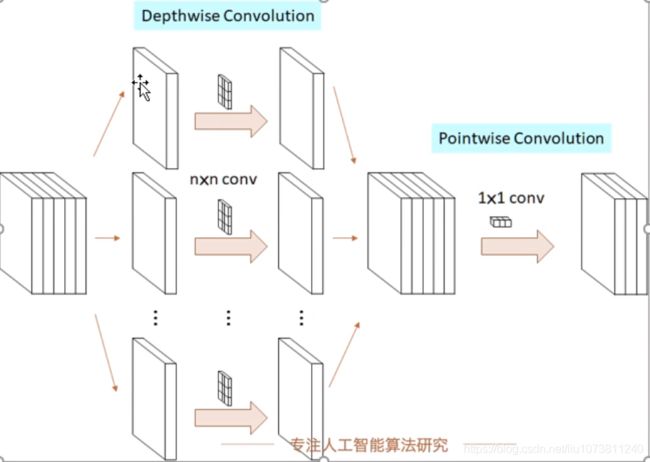
八：MobileNet

8.1 MobileNet-v1

一句话概括，V1 就是把 vgg中标准卷积层换成了深度可分离卷积；

1. 深度可分离卷积，大大减少参数量

2. 增加超参 α、β
   

8.2 MobileNet-v2

MobileNetV2 是由谷歌 在 2018 年提出，相比 V1，准确率更好，模型更小；

模型亮点：

1. Inverted Residuals（倒残差结构）

2. Linear bottlenecks
   

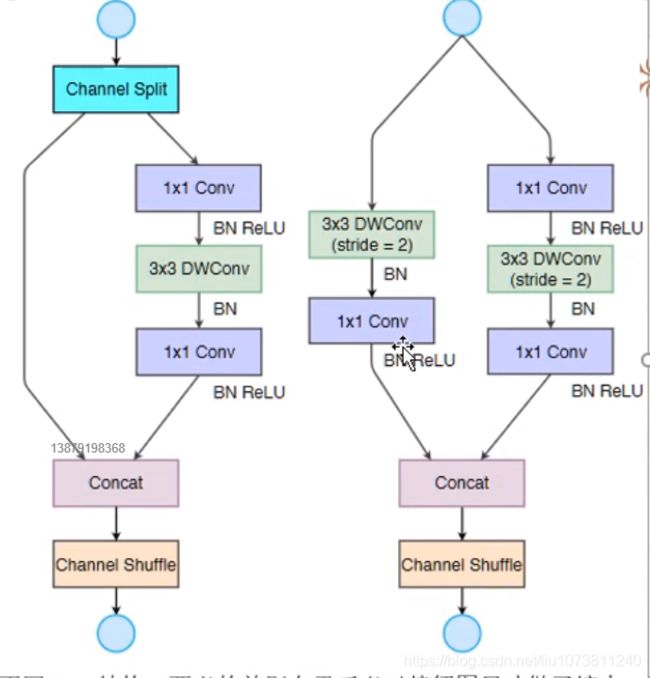
九：ShuffelNet

9.1 ShuffelNet-v1

       ShuffleNet的核心是采用了两种操作：pointwise group convolution和channel shuffle，这在保持精度的同时大大降低了模型的计算量。其基本单元则是在一个残差单元的基础上改进而成。

10.ShuffelNet-v2

(1) 卷积层的输入和输出特征通道数相等时MAC最小，此时模型速度最快.

(2) 过多的group操作会增大MAC，从而使模型速度变慢.

(2) 模型中的分支数量越少，模型速度越快.

(3) element-wise操作所带来的时间消耗远比在FLOPs上的体现的数值要多，因此要尽可能减少element-wise操作.

十：EfficientNet

1.探索

       卷积神经网络(ConvNets)通常是在固定的资源预算下开发的，如果有更多的资源可用，就会扩大规模以获得更好的准确性。作者系统地研究了模型缩放，发现平衡网络的深度、宽度和分辨率可以得到更好的性能。在此基础上，作者提出了一种新的尺度划分方法，即利用简单而高效的复合系数来均匀地划分深度/宽度/分辨率各维度。

       作者希望找到一个可以同时兼顾速度与精度的模型放缩方法，为此，作者重新审视了前人提出的模型放缩的几个维度:网络深度、网络宽度、图像分辨率，前人的文章多是放大其中的一一个维度以达到更高的准确率，比如ResNet-18到ResNet-152是通过增加网络深度的方法来提高准确率工作者跳出了前人对放缩模型的理解，从一个高度去审视这砦放缩维度，作者认为这三个维度之间是互相影响的并探索出了三者之间最好的组合，在此基础上提出了最新的网络EfficientNet (基于神经网络搜索)。

2. 提出第一个问题，实验得出结论

       那么第一个问题就是:单个维度做scaling存在什么问题吗?针对这个问题，作者做了这个实验，也就是针对某个分类网络的3个维度(宽度、深度和分辨率)分别做model scaling的结果对比。显然，单独优化这3个维度都能提升模型效果，但上限也比较明显，基本上在Acc达到80后提升就很小了。

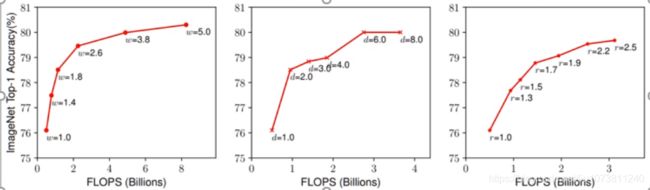
1、单纯增加层数(深度d)和精度的增加变化呈log函数，也就是说深度达到一定程度后，精度的增加就很小了，但是参数量却还在不断变大。
2、同理，只对通道(宽度w)的增加也和精度的增加变化呈log函数。
3、输入图像(分辨率r)越大，精度越高，但是它们之间也呈log函数。

       结论: 三个维度中任一维度的放大都可以带来精度的提开，但随着倍率越来越大，提升却越来越小。

       由于对单个维度的缩放存在问题，作者做了第二个实验，尝试在不同的d,r组合下变动w，得到上图。

       从实验结果可以看出最高精度比之前已经有所提升，且不同的组合效果还不一样，最高可以到82左右。作者又得到一个观点，得到更高的精度以及效率的关键是平衡网络宽度，网络深度，图像分辨率三个维度的放缩倍率(d, r, w)。

3. 提出第二个问题，实验得出结论

       问题:需要找到平衡参数(分辨率、深度、宽度)和精度之间的指标。既满足参数量少，又满足精度高。如果简单的根据给定上面的3个参数参数设计模型进行训练，显然是不可行的，这样的效率太低下。

       作者提出了一种混合维度放大法(compound scaling method)，该方法使用一个混合系数，先设计搜索一个较小(深度d和宽度w)的网络做为基础网络，传入较小的图片(分辨率r，一般为224)，先获得比较好的精度，然后增加一定的深度倍数a、宽度倍数β、分辨率倍数γ，在参数计算量增加2倍，并且精度最高的情况下搜索到了一组最佳的参数a=1.2,B=1.1,y=1.15，参数即满足公式: a*β^2 *γ^2≈2, (a≥1, β≥1, Y≥1)。

4.发现规律

       其中，a, γ, β均为常数(不是无限大的因为三者对应了计算量)，可通过网格搜索获得。混合系数φ可以人工调节。

       d、w和r参数对FLOPS计算的影响，以卷积层为例，假如d变成原来的2倍，那么FLOPS也会变成原来的2倍;假如w变成原来的2倍，那么FLOPS就变成原来的4倍，因为输入输出通道都变成原来的2倍了，所以在计算量方面相当于4倍; r和w一样，如果r变成原来的2倍，那么计算量也会变成原来的4倍，由于输入的图像变成了原来的2倍，所以输出特征图的宽和高都变成原来的2倍了。

       即卷积操作的计算量(FLOPS)与d^2， R^2 成正比，因此上图中的约束条件中有两个平方项。在该约束条件下，指定混合系数中之后，网络的计算量大概会是之前的2φ倍。

5.提出网络结构

       有了第一代的网络结构BfficientNet-b0之后，对模型扩张的参数调整可以分为两步第一步，首先固定中为1,即设定计算量为原来的2倍，在这样一个小模型上做网格搜索(grid search)， 得到了最佳系数为a=1.2,p=1.1,y=1.15。
       第二步，固定a=1.2,β=1.1,y=1.15，使用不同的混合系数中来放大初代网络得到EfficientNet-B1，EfficientNet-B7.