LeNet-ResNet-AlexNet网络详解
LeNet-ResNet-AlexNet
- LeNet
-
- pytorch实现
- ResNet
-
- pytorch实现
- AlexNet
-
- pytorch实现
LeNet
学习lenet-5的过程中,发现了一个可视化的网站
手写数字识别可视化网站

-
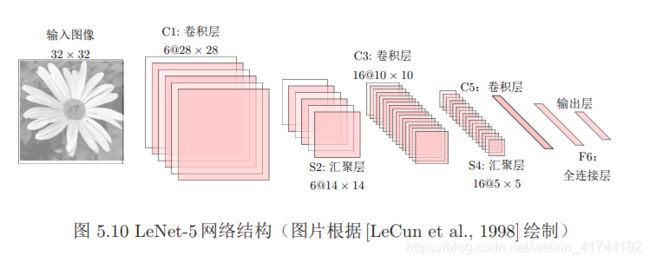
输入层:输入图像的尺寸统一归一化为32*32。
-
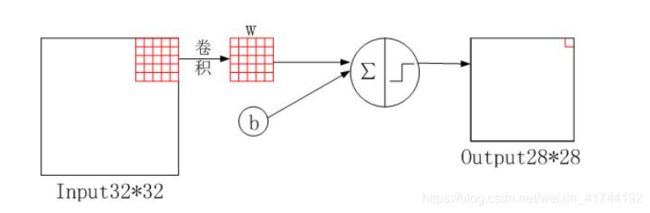
C1层-卷积层
输入图片:3232
卷积核大小:55
卷积核种类:6
输出feature map大小:2828 (32-5+1)=28
神经元数量:28286
可训练参数:(55+1) * 6(每个滤波器55=25个unit参数和一个bias参数,一共6个滤波器)
连接数:(55+1)62828=122304
详细说明:对输入图像进行第一次卷积运算(使用 6 个大小为 55 的卷积核),得到6个C1特征图(6个大小为2828的 feature maps, 32-5+1=28)。我们再来看看需要多少个参数,卷积核的大小为55,总共就有6*(55+1)=156个参数,其中+1是表示一个核有一个bias。对于卷积层C1,C1内的每个像素都与输入图像中的55个像素和1个bias有连接,所以总共有1562828=122304个连接(connection)。有122304个连接,但是我们只需要学习156个参数,主要是通过权值共享实现的。
-
S2层-池化层(下采样层)
输入:2828
采样区域:22
采样方式:4个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过sigmoid
采样种类:6
输出feature Map大小:1414(28/2)
神经元数量:14146
连接数:(22+1)61414
S2中每个特征图的大小是C1中特征图大小的1/4。
详细说明:第一次卷积之后紧接着就是池化运算,使用 22核 进行池化,于是得到了S2,6个1414的 特征图(28/2=14)。S2这个pooling层是对C1中的22区域内的像素求和乘以一个权值系数再加上一个偏置,然后将这个结果再做一次映射。同时有5x14x14x6=5880个连接。

-
C3层-卷积层
输入:S2中所有6个或者几个特征map组合
卷积核大小:55
卷积核种类:16
输出feature Map大小:1010 (14-5+1)=10
C3中的每个特征map是连接到S2中的所有6个或者几个特征map的,表示本层的特征map是上一层提取到的特征map的不同组合存在的一个方式是:C3的前6个特征图以S2中3个相邻的特征图子集为输入。接下来6个特征图以S2中4个相邻特征图子集为输入。然后的3个以不相邻的4个特征图子集为输入。最后一个将S2中所有特征图为输入。则:可训练参数:6*(355+1)+6*(455+1)+3*(455+1)+1*(655+1)=1516
连接数:10101516=151600
怎么从6 个特征图得到 16个特征图了?
这里是通过对S2 的特征图特殊组合计算得到的16个特征图。C3的前6个feature map(对应上图第一个红框的6列)与S2层相连的3个feature map相连接(上图第一个红框),后面6个feature map与S2层相连的4个feature map相连接(上图第二个红框),后面3个feature map与S2层部分不相连的4个feature map相连接,最后一个与S2层的所有feature map相连。具体如下:
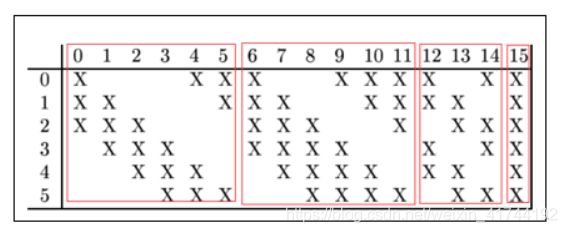
通过S2的输入,如何卷积得到C3的一个特征图?
我用C3层0号特征图举例,它由S2层0,1,2号特征图作为输入,由于C3层共有16个卷积核,即C3每一个特征图是由一个卷积核对S2层相应的输入特征图卷积得到的,这里值得注意的是,下图的一个卷积核是一个5×5大小具有3个通道,每个通道各不相同,这也是下面计算时55后面还要乘以3,4,4,6的原因。具体可参考多通道卷积。
参数个数:(553+1)6+(554+1)6+(554+1)3+(556+1)=1516
连接数:15161010=151600

为什么采用上述这样的组合了?论文中说有两个原因:
1)减少参数,
2)这种不对称的组合连接的方式有利于提取多种组合特征。
- S4层是一个池化层,采样窗口为2 × 2,得到16个5 × 5大小的特征映射,可训练参数数量为16 × 2 = 32,连接数为16 × 25 × (4 + 1) = 2000。
- C5层是一个卷积层,使用120 × 16 = 1,920个5 × 5的滤波器,得到120组大小为1 × 1的特征映射,这里的计算跟C3相同,也是多通道卷积,因此5*5后面乘以16。C5层的神经元数量为120,可训练参数数量为1, 920 × 25 + 120 = 48,120,连接数为120 × (16 × 25 + 1) = 48120。
- F6层是一个全连接层,有84个神经元,可训练参数数量为84×(120+1) =10, 164。连接数和可训练参数个数相同,为10164。
- 输出层:Output层也是全连接层,共有10个节点,分别代表数字0到9,且如果节点i的值为0,则网络识别的结果是数字i。采用的是径向基函数(RBF)的网络连接方式。假设x是上一层的输入,y是RBF的输出,则RBF输出的计算方式是:

上式w_ij 的值由i的比特图编码确定,i从0到9,j取值从0到7*12-1。RBF输出的值越接近于0,则越接近于i,即越接近于i的ASCII编码图,表示当前网络输入的识别结果是字符i。该层有84x10=840个参数和连接。
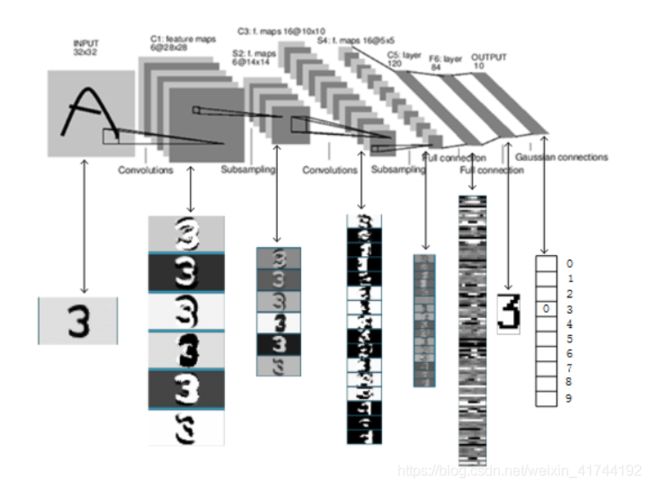
上图是LeNet-5识别数字3的过程。
pytorch实现
import time
import torch
from torch import nn, optim
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
device = torch.device('cuda' if torch.cuda.is_available() else
'cpu')
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(1, 6, 5), # in_channels, out_channels,kernel_size
nn.Sigmoid(),
nn.MaxPool2d(2, 2), # kernel_size, stride
nn.Conv2d(6, 16, 5),
nn.Sigmoid(),
nn.MaxPool2d(2, 2)
)
self.fc = nn.Sequential(
nn.Linear(16*4*4, 120),
nn.Sigmoid(),
nn.Linear(120, 84),
nn.Sigmoid(),
nn.Linear(84, 10)
)
def forward(self, img):
feature = self.conv(img)
output = self.fc(feature.view(img.shape[0], -1))
return output
ResNet
对神经⽹络模型添加新的层,充分训练后的模型是否只可能更有效地降低训练误差?
理论上,原模型解的空间只是新模型解的空间的⼦空间。也就是说,如果我们能将新添加的层训练成恒等映射 ,新模型和原模型将同样有效。由于新模型可能得出更优的解来拟合训练数据集,因此添加层似乎更容易降低训练误差。然⽽在实践中,添加过多的层后训练误差往往不降反升。即使利⽤批量归⼀化带来的数值稳定性使训练深层模型更加容易,该问题仍然存在。针对这⼀问题,何恺明等⼈提出了残差⽹络(ResNet。它在2015年的ImageNet图像识别挑战赛夺魁,并深刻影响了后来的深度神经⽹络的设计。
让我们聚焦于神经⽹络局部。如图5.9所示,设输⼊为 。假设我们希望学出的理想映射为 ,从⽽作为图5.9上⽅激活函数的输⼊。左图虚线框中的部分需要直接拟合出该映射 ,⽽右图虚线框中的部分则需要拟合出有关恒等映射的残差映射 。残差映射在实际中往往更容易优化。以本节开头提到的恒等映射作为我们希望学出的理想映射 。我们只需将图5.9中右图虚线框内上⽅的加权运算(如仿射)的权᯿和偏差参数学成0,那么 即为恒等映射。实际中,当理想映射 极接近于恒等映射时,残差映射也易于捕捉恒等映射的细微波动。图5.9右图也是ResNet的基础块,即残差块(residual block)。在残差块中,输⼊可通过跨层的数据线路更快地向前传播。

pytorch实现
残差块
import time
import torch
from torch import nn, optim
import torch.nn.functional as F
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
device = torch.device('cuda' if torch.cuda.is_available() else'cpu')
class Residual(nn.Module):
# 本类已保存在d2lzh_pytorch包中⽅便以后使⽤
def __init__(self, in_channels, out_channels,use_1x1conv=False, stride=1):
super(Residual, self).__init__()
self.conv1 = nn.Conv2d(in_channels, out_channels,
kernel_size=3, padding=1, stride=stride)
self.conv2 = nn.Conv2d(out_channels, out_channels,
kernel_size=3, padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(in_channels, out_channels,
kernel_size=1, stride=stride)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(out_channels)
self.bn2 = nn.BatchNorm2d(out_channels)
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
return F.relu(Y + X)
下面我们来查看输⼊和输出形状⼀致的情况。
blk = Residual(3, 3)
X = torch.rand((4, 3, 6, 6))
blk(X).shape # torch.Size([4, 3, 6, 6])
我们也可以在增加输出通道数的同时减半输出的⾼和宽。
blk = Residual(3, 6, use_1x1conv=True, stride=2)
blk(X).shape # torch.Size([4, 6, 3, 3])
AlexNet
2012年,AlexNet横空出世。这个模型的名字来源于论⽂第⼀作者的姓名Alex Krizhevsky 。AlexNet使⽤了8层卷积神经⽹络,并以很⼤的优势赢得了ImageNet 2012图像识别挑战赛。它⾸次证明了学习到的特征可以超越⼿⼯设计的特征,从⽽⼀举打破计算机视觉研究的前状。
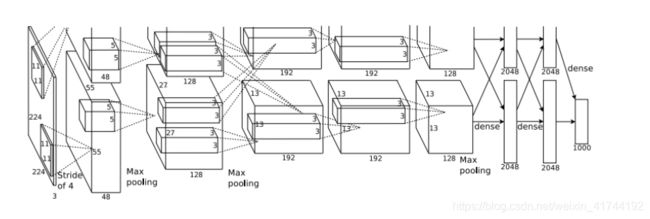
AlexNet的具体结构如下: 这里的卷积核使用四维张量来描述。
- 输入层,224 × 224 × 3的图像;
- 第一个卷积层,使用两个11 × 11 × 3 × 48的卷积核,步长s = 4,零填充p = 3,得到两个55 × 55 × 48的特征映射组。
- 第一个汇聚层,使用大小为3 × 3的最大汇聚操作,步长s = 2,得到两个27 × 27 × 48的特征映射组。
- 第二个卷积层,使用两个 5 × 5 × 48 × 128的卷积核,步长s = 1,零填充p = 1,得到两个27 × 27 × 128的特征映射组。
- 第二个汇聚层,使用大小为3 × 3的最大汇聚操作,步长s = 2,得到两个13 × 13 × 128的特征映射组。
- 第三个卷积层为两个路径的融合,使用一个 3 × 3 × 256 × 384的卷积核,步长s = 1,零填充p = 1,得到两个13 × 13 × 192的特征映射组。
- 第四个卷积层,使用两个 3 × 3 × 192 × 192的卷积核,步长s = 1,零填充p = 1,得到两个13 × 13 × 192的特征映射组。
- 第五个卷积层,使用两个 3 × 3 × 192 × 128的卷积核,步长s = 1,零填充p = 1,得到两个13 × 13 × 128的特征映射组。
- 汇聚层,使用大小为3×3的最大汇聚操作,步长s = 2,得到两个6×6×128的特征映射组。
- 三个全连接层,神经元数量分别为4096,4096和1000。
AlexNet与LeNet的设计理念⾮常相似,但也有显著的区别。
第⼀,与相对较⼩的LeNet相⽐,AlexNet包含8层变换,其中有5层卷积和2层全连接隐藏层,以及1个全连接输出层。下⾯我们来详细描述这些层的设计。AlexNet第⼀层中的卷积窗⼝形状是 。因为ImageNet中绝⼤多数图像的⾼和宽均⽐MNIST图像的⾼和宽⼤10倍以上,ImageNet图像的物体占⽤更多的像素,所以需要更⼤的卷积窗⼝来捕获物体。第⼆层中的卷积窗⼝形状减⼩到 ,之后全采⽤ 。此外,第⼀、第⼆和第五个卷积层之后都使⽤了窗⼝形状为 、步幅为2的最⼤池化层。⽽且,AlexNet使⽤的卷积通道数也⼤于LeNet中的卷积通道数数⼗倍。紧接着最后⼀个卷积层的是两个输出个数为4096的全连接层。这两个巨⼤的全连接层带来将近1 GB的模型参数。由于早期显存的限制,最早的AlexNet使⽤双数据流的设计使⼀个GPU只需要处理⼀半模型。幸运的是,显存在过去⼏年得到了⻓⾜的发展,因此通常我们不再需要这样的特别设计了。
第⼆,AlexNet将sigmoid激活函数改成了更加简单的ReLU激活函数。⼀⽅⾯,ReLU激活函数的计算更简单,例如它并没有sigmoid激活函数中的求幂运算。另⼀⽅⾯,ReLU激活函数在不同的参数初始化⽅法下使模型更容易训练。这是由于当sigmoid激活函数输出极接近0或1时,这些区域的梯度⼏乎为0,从⽽造成反向传播⽆法继续更新部分模型参数;⽽ReLU激活函数在正区间的梯度恒为1。因此,若模型参数初始化不当,sigmoid函数可能在正区间得到⼏乎为0的梯度,从⽽令模型⽆法得到有效训练。
第三,AlexNet通过丢弃法来控制全连接层的模型复杂度。⽽LeNet并没有使⽤丢弃法。
第四,AlexNet引⼊了⼤量的图像增⼴,如翻转、裁剪和颜⾊变化,从⽽进⼀步扩⼤数据集来缓解过拟合。
pytorch实现
简化过的AlexNet。
class AlexNet(nn.Module):
def __init__(self):
super(AlexNet, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(1, 96, 11, 4), # in_channels, out_channels,kernel_size, stride, padding
nn.ReLU(),
nn.MaxPool2d(3, 2), # kernel_size, stride
# 减⼩卷积窗⼝,使⽤填充为2来使得输⼊与输出的⾼和宽⼀致,且增⼤输出通道数
nn.Conv2d(96, 256, 5, 1, 2),
nn.ReLU(),
nn.MaxPool2d(3, 2),
# 连续3个卷积层,且使⽤更⼩的卷积窗⼝。除了最后的卷积层外,进⼀步增⼤了输出通道数。
# 前两个卷积层后不使⽤池化层来减⼩输⼊的⾼和宽
nn.Conv2d(256, 384, 3, 1, 1),
nn.ReLU(),
nn.Conv2d(384, 384, 3, 1, 1),
nn.ReLU(),
nn.Conv2d(384, 256, 3, 1, 1),
nn.ReLU(),
nn.MaxPool2d(3, 2)
)
# 这⾥全连接层的输出个数⽐LeNet中的⼤数倍。使⽤丢弃层来缓解过拟合
self.fc = nn.Sequential(
nn.Linear(256*5*5, 4096),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(4096, 4096),
nn.ReLU(),
nn.Dropout(0.5),
# 输出层。由于这⾥使⽤Fashion-MNIST,所以⽤类别数为10,⽽⾮论⽂中的1000
nn.Linear(4096, 10),
)
def forward(self, img):
feature = self.conv(img)
output = self.fc(feature.view(img.shape[0], -1))
return output