A*算法实现全局路径规划——基于python

A*算法简介

一种在已知地图、目标点和起始点的情况下，寻找最短路径的启发式算法。

数学表达式：核心在于计算F值
$$F=G+H$$
其中：
F：为总移动代价
G：起点到当前点的代价（已经发生的代价）
H：当前点到目标点的代价（尚未发生，人为预估的代价）

H值的计算可用欧拉距离或曼哈顿距离等
启发函数的定义需体现出“引导性”，能够“引导”粒子向目标点移动

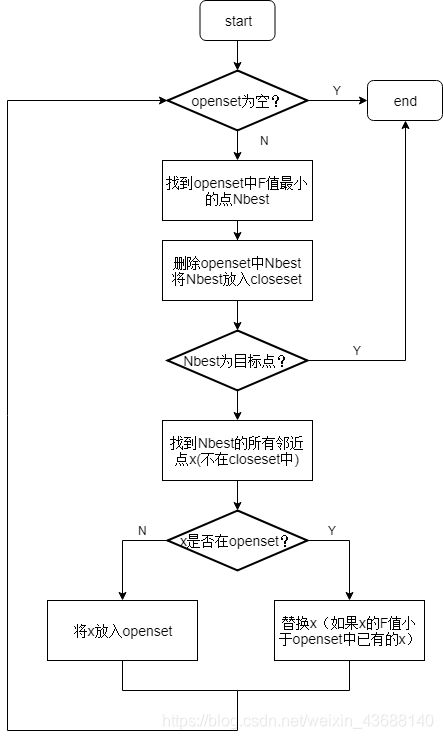
算法实现思路

python代码实现

"""
	Author: Tomanlon

	Copyright: Tomanlon

	Date: 2019-3-9

	Description: Simple demo for displaying astar algorithm with path find

	MailBox: [email protected]
"""
"""
	Author：Zheng Yeping
	Data：2021-6-5
	Description：Add some details about the code
"""

import matplotlib.pyplot as plt
import math

#define node

#定义Node节点类
#坐标、父节点、代价、索引
class Node:
	def __init__(self,x,y,parent,cost,index):
		self.x = x
		self.y = y
		#used for tracking path node in closeset
		self.parent = parent
		self.cost = cost
		# node index
		self.index = index

# tracking path node
# 计算路径上所有点的坐标
# 父结点的作用：保证封闭列表中，节点的顺序性
def calc_path(goaln,closeset):
	rx,ry=[goaln.x],[goaln.y]
	print (closeset[-1])
	#goal parent node in closeset
	parentn = closeset[-1]

	while parentn!=None:
		rx.append(parentn.x)
		ry.append(parentn.y)
		parentn = parentn.parent
	return rx,ry


# astar algorithm core
def astar_plan(sx,sy,gx,gy):
	# 生成地图
	# ox,oy为障碍物坐标点
	# xwidth,ywidth为地图的长和宽
	ox,oy,xwidth,ywidth=map_generation()
	# show map
	plt.figure('Astar algorithm demo')
	plt.plot(ox,oy,'ks')
	plt.plot(sx,sy,'bs')
	plt.plot(gx,gy,'ro')
	#定义每个点的可运动方向（8个）
	motion = motion_model()
	# 初始化开放列表与封闭列表
	openset,closeset=dict(),dict()
	sidx = sy*xwidth+sx
	gidx = gy*xwidth+gx
	# start node and goal node
	#Node(x,y,父节点,代价,索引)
	starn=Node(sx,sy,None,0,sidx)
	goaln=Node(gx,gy,None,0,gidx)
	#起点放入开放列表
	openset[sidx] = starn
	while 1:
		# calculate node with min f_cost as current node
		# h_cost()是启发函数，评估当前点到目标点的代价
		c_id = min(openset,key=lambda o:openset[o].cost + h_cost(openset[o],goaln))

		#代价F值最小的点，作为考察节点
		curnode = openset[c_id]
		# if arrive goal point break else closset add current node and remove current node from openset
		if curnode.x == goaln.x and curnode.y == goaln.y:
			print ('find goal')
			closeset[-1] = curnode
			break
		else:
			closeset[c_id] = curnode	
			plt.plot(curnode.x,curnode.y,'gx')
			if len(openset.keys())%10==0:
				plt.pause(0.01)
			del openset[c_id]
		
		# check 8 direction point
		for j in range(len(motion)):
			newnode = Node(curnode.x+motion[j][0],
						   curnode.y+motion[j][1],
						   curnode, #新节点的父结点为当前节点
						   curnode.cost + motion[j][2], # F=G+H，已知代价（已经发生的）加上预估代价
						   c_id)
			# 计算新节点的索引值
			n_id = index_calc(newnode,xwidth)
			
			# if node in closeset out of loop once
			# 新节点在封闭列表中，则跳过
			if n_id in closeset:
				continue
			
			# 新节点是障碍物，则跳过
			if node_verify(newnode,ox,oy):
				continue
			
			# 新节点不在开放列表，则立即加入开放列表
			# 新节点在开放列表，则比较该节点的F值；如果新节点的F值更小，则替换
			if n_id not in openset:
				openset[n_id] = newnode
			else:
				# id对应唯一的点，但到达该点的方式有很多，不同的方式对应不同的父结点和代价G
				# 更新openset已有点，主要是更新点的父结点和已发生代价值G
				if openset[n_id].cost >= newnode.cost:
					openset[n_id] = newnode
	# get path node x ,y 
	px,py = calc_path(goaln,closeset)
	return px,py

#初始化地图
#产生地图数据障碍物坐标点(ox,oy)
def map_generation():
	# ox,oy list for obstacles
	ox,oy=[],[]
	#边界
	for i in range(60):
		ox.append(i)
		oy.append(0)

	for i in range(60):
		ox.append(i)
		oy.append(60)

	for i in range(60):
		ox.append(0)
		oy.append(i)

	for i in range(60):
		ox.append(60)
		oy.append(i)

	#障碍物坐标
	for i in range(25):
		ox.append(i)
		oy.append(20)

	for i in range(40):
		ox.append(35)
		oy.append(i)

	for i in range(40):
		ox.append(50)
		oy.append(60-i)

	minx = min(ox)
	miny = min(oy)
	maxx = max(ox)
	maxy = max(oy)
	# map  xwidth,  ywidth
	xwidth = maxx-minx
	ywidth = maxy-miny
	
	return ox,oy,xwidth,ywidth
	

	
# motion model in 8 direction with 8 g_costs
# 定义运动模型，向每个节点的8个方向运动，并产生运动代价
def motion_model():
	motion =[[1,0,1],
			 [1,1,math.sqrt(2)],
			 [1,-1,math.sqrt(2)],
			 [0,1,1],
			 [0,-1,1],
			 [-1,1,math.sqrt(2)],
			 [-1,0,1],
			 [-1,-1,math.sqrt(2)]]
	return motion

#定义评价函数，当前点到目的点的预估代价
#可采用欧氏距离或曼哈顿距离
#曼哈顿距离：两点在坐标系上轴距之和|x1-x0|+|y1-y0|
#欧式距离：直线距离
def h_cost(node,goal):
	# Weight
	w = 1.0
	#h = w*math.sqrt((goal.x-node.x)**2 + (goal.y-node.y)**2)
	# Mahattan distance
	h = w*(abs(goal.x-node.x) + abs(goal.y-node.y))
	return h

# Node index obtain
# 计算节点索引，感觉是将二维转化为一维
def index_calc(node,xwid):
	n_id = node.y*xwid + node.x
	return n_id

# Verify node is in obstacle or not
#判断节点是否为障碍物
def node_verify(node,ox,oy):
	if (node.x,node.y) in zip(ox,oy):
		return True
	else:
		return False

def main():
	# Define  start point(sx,sy),goal point(gx,gy)
	sx,sy=15,15
	gx,gy=55,50
	# Astar algorithm tracking path node
	rx,ry=astar_plan(sx,sy,gx,gy)
	print (rx,ry)
	# show path
	plt.plot(rx,ry,'r-',linewidth=3)
	plt.show()


if __name__ =="__main__":
	main()

参考文献

[1] 陶满礼. ROS机器人编程与SLAM算法解析指南[M]. 北京：人民邮电出版社