机器学习之KNN算法
文章目录
- 前言
- 一、KNN算法概述
- 二、KNN算法介绍
-
- 距离量度
-
- 闵可夫斯基距离
- 欧氏距离
- 曼哈顿距离
- 三、 KNN特点
-
- KNN算法的优势和劣势
-
- KNN算法优点
- KNN算法缺点
- 四、 實戰
- 總結
前言
随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文就介绍了机器学习的基础内容。
一、KNN算法概述
KNN可以说是最简单的分类算法之一,同时,它也是最常用的分类算法之一,注意KNN算法是有监督学习中的分类算法,它看起来和另一个机器学习算法Kmeans有点像(Kmeans是无监督学习算法),但却是有本质区别的。最明顯的區別就是他是需要標簽的
二、KNN算法介绍
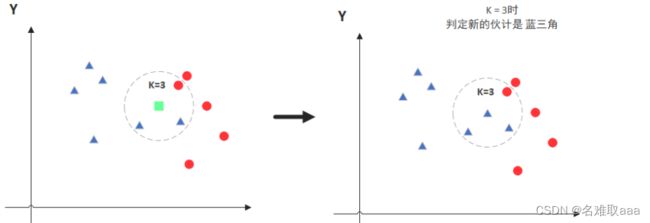
KNN的全称是K Nearest Neighbors,意思是K个最近的邻居,从这个名字我们就能看出一些KNN算法的蛛丝马迹了。K个最近邻居,毫无疑问,K的取值肯定是至关重要的。那么最近的邻居又是怎么回事呢?其实啊,KNN的原理就是当预测一个新的值x的时候,根据它距离最近的K个点是什么类别来判断x属于哪个类别
图中绿色的点就是我们要预测的那个点,假设K=3那么KNN算法就会找到与它距离最近的三个点(这里用圆圈把它圈起来了),看看哪种类别多一些,比如这个例子中是蓝色三角形多一些,新来的绿色点就归类到蓝三角了。
但是,当K=5的时候,判定就变成不一样了。这次变成红圆多一些,所以新来的绿点被归类成红圆。从这个例子中,我们就能看得出K的取值是很重要的。
距离量度
样本空间内的两个点之间的距离量度表示两个样本点之间的相似程度:距离越短,表示相似程度越高;反之,相似程度越低。
常用的距离量度方式包括:
-
闵可夫斯基距离
-
欧氏距离
-
曼哈顿距离
-
切比雪夫距离
-
余弦距离
闵可夫斯基距离
闵可夫斯基距离本身不是一种距离,而是一类距离的定义。对于n维空间中的两个点x(x1,x2,…,xn)和y(y1,y2,…,yn),x和y之间的闵可夫斯基距离可以表示为:
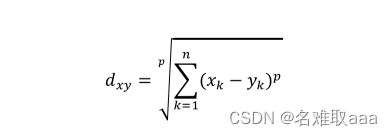
其中,p是一个可变参数:
当p=1时,被称为曼哈顿距离;
当p=2时,被称为欧氏距离;
当p=\infty时,被称为切比雪夫距离。
欧氏距离
根据以上定义,欧氏距离可以写为

欧氏距离(L2范数)是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式,也是最常用的距离量度。
曼哈顿距离
根据闵可夫斯基距离定义,曼哈顿距离的计算公式可以写为:
三、 KNN特点
KNN是一种非参的,惰性的算法模型。什么是非参,什么是惰性呢?
非参的意思并不是说这个算法不需要参数,而是意味着这个模型不会对数据做出任何的假设,与之相对的是线性回归(我们总会假设线性回归是一条直线)。也就是说KNN建立的模型结构是根据数据来决定的,这也比较符合现实的情况,毕竟在现实中的情况往往与理论上的假设是不相符的。
惰性又是什么意思呢?想想看,同样是分类算法,逻辑回归需要先对数据进行大量训练(tranning),最后才会得到一个算法模型。而KNN算法却不需要,它没有明确的训练数据的过程,或者说这个过程很快。
KNN算法的优势和劣势
KNN算法优点
- 简单易用,相比其他算法,KNN算是比较简洁明了的算法。即使没有很高的数学基础也能搞清楚它的原理。
- 模型训练时间快,上面说到KNN算法是惰性的,这里也就不再过多讲述。
- 预测效果好。
- 对异常值不敏感
KNN算法缺点
- 对内存要求较高,因为该算法存储了所有训练数据
- 预测阶段可能很慢
- 对不相关的功能和数据规模敏感
四、 實戰
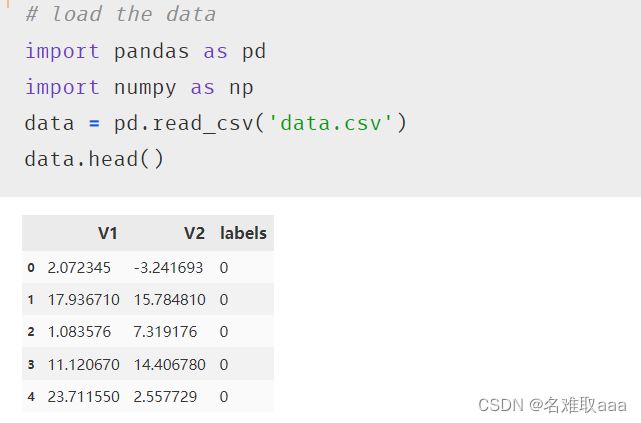
# load the data
import pandas as pd
import numpy as np
data = pd.read_csv('data.csv')
data.head()
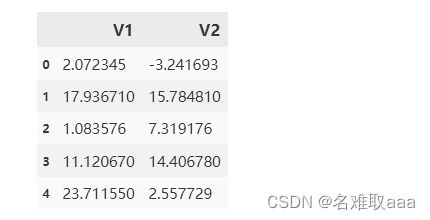
#define X and y
X = data.drop(['labels'],axis=1)
y = data.loc[:,'labels']
X.head()
from matplotlib import pyplot as plt
fig1 = plt.figure()
plt.scatter(X.loc[:,'V1'],X.loc[:,'V2'])
plt.title('un-labled data')
plt.xlabel('V1')
plt.ylabel('V2')
plt.show()
可視化看一下原始數據
fig2 = plt.figure()
lable0 = plt.scatter(X.loc[:,'V1'][y==0],X.loc[:,'V2'][y==0])
lable1 = plt.scatter(X.loc[:,'V1'][y==1],X.loc[:,'V2'][y==1])
lable2 = plt.scatter(X.loc[:,'V1'][y==2],X.loc[:,'V2'][y==2])
plt.title('labled data')
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((lable0,lable1,lable2),('lable0','lable1','lable2'))
plt.show()
加上標簽可視化
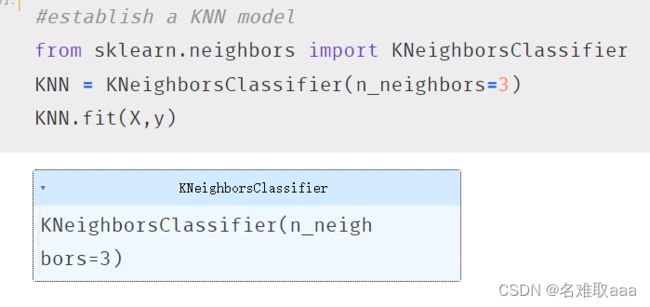
#establish a KNN model
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X,y)
訓練模型
#predict based on the test data V1=80, V2=60
y_predict_knn_test = KNN.predict([[80,60]])
y_predict_knn = KNN.predict(X)
print(y_predict_knn_test)
print('knn accuracy:',accuracy_score(y,y_predict_knn))
測試模型和看一下accuracy_score,可以看出預測還是比較好
fig6 = plt.subplot(121)
lable0 = plt.scatter(X.loc[:,'V1'][y_predict_knn==0],X.loc[:,'V2'][y_predict_knn==0])
lable1 = plt.scatter(X.loc[:,'V1'][y_predict_knn==1],X.loc[:,'V2'][y_predict_knn==1])
lable2 = plt.scatter(X.loc[:,'V1'][y_predict_knn==2],X.loc[:,'V2'][y_predict_knn==2])
plt.title('knn results')
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((lable0,lable1,lable2),('lable0','lable1','lable2'))
plt.scatter(centers[:,0],centers[:,1])
fig7 = plt.subplot(122)
lable0 = plt.scatter(X.loc[:,'V1'][y==0],X.loc[:,'V2'][y==0])
lable1 = plt.scatter(X.loc[:,'V1'][y==1],X.loc[:,'V2'][y==1])
lable2 = plt.scatter(X.loc[:,'V1'][y==2],X.loc[:,'V2'][y==2])
plt.title('labled data')
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((lable0,lable1,lable2),('lable0','lable1','lable2'))
plt.scatter(centers[:,0],centers[:,1])
plt.show()
總結
這就是本次學習KNN的筆記
附上數據集和源碼
鏈接:https://github.com/fbozhang/python/tree/master/jupyter