【联邦学习论文阅读】FedAvg(2016)Communication-Efficient Learning of Deep Networks from Decentralized Data
【FedAvg】论文链接:https://arxiv.org/abs/1602.05629
摘要
移动通信设备中有许多有用的数据,训练模型后可以提高用户体验。但是,这些数据通常敏感或很庞大,不能直接上传到数据中心,使用传统的方法训练模型。据此提出联邦学习,将训练数据分布在移动设备上,通过聚合本地计算的更新来学习共享模型。
考虑了5种不同的模型和4个数据集,证明本文的方法对不平衡和非独立同分布的数据是鲁棒的,且降低了通信成本。
一、介绍
主要贡献:
- 将移动设备的去中心化数据的训练作为重要研究方向
- 选择可以应用的简单而实用的算法
- 对所提出的方法进行广泛的实证评估
1.联邦学习的理想问题具有以下特性:
- 训练来自移动设备的真实数据比数据中心提供的代理数据具有明显优势;
- 数据是隐私敏感或较大规模的,最好不要仅出于训练模型的目的将其记录在数据中心;
- 对于监督任务,可以从用户交互中自然地推断出数据的标签。
许多移动设备上的智能应用有满足上述标准的数据,如 图像分类 和 语言模型。两个任务都非常适合学习神经网络:前者有前馈深层网络,特别是卷积网络;后者有循环神经网络,特别是LSTM。
2.与数据中心训练持久数据相比,联邦学习具有明显的隐私优势:
- 联邦学习传输的信息是改进特定模型所必需的最小更新(隐私利益的强度取决于更新的内容);
- 更新本身是短暂的,所包含的信息绝不会超过原始训练数据且通常会少得多;
- 聚合算法不需要更新源,因此无需识别元数据,就可以通过混合网络(例如Tor)或可信第三方传输更新;
- 在本文的最后,简要地讨论了将联合学习与安全的多方计算和差分隐私相结合的可能性。
3.联邦优化问题的关键(对比分布式优化问题)
- 客户端数据非独立同分布: 特定的用户数据不能代表整体用户的数据分布;
- 客户端数据量不平衡: 数据量不均衡,有的用户多,有的用户少;
- 客户端(分布)是大规模的: 参与优化的用户数>平均每个用户的数据量;
- 客户端设备通信限制: 移动设备经常掉线、速度缓慢、费用昂贵。
实际部署的联邦优化系统还须解决许多实际问题:
- 随着数据添加和删除而不断改变的客户端数据集;
- 客户端(更新)的可用性与其本地数据分布有着复杂的关系;
- 从来不响应或发送信息的客户端会损坏更新。
这些实际问题超出了当前工作的范围,本文使用了适合实验的可控环境,且解决了客户端可用性、不平衡和non-IID数据的关键问题。
【非凸神经网络的目标函数】
一般的机器学习或深度学习中,最终的目标都是最小化所有样本的损失函数( f i ( w ) = ℓ ( x i , y i ; w ) f_i(w)=\ell(x_i,y_i;w) fi(w)=ℓ(xi,yi;w) 是损失函数,n是样本数量,w是训练的模型参数): m i n w ∈ R d f ( w ) where f ( w ) = d e f 1 n ∑ i = 1 n f i ( w ) \underset{w\in \mathbb{R}^d}{min}\ f(w)\ \texttt{where} \ f(w)\overset{def}{=}\frac{1}{n}\sum_{i=1}^{n}f_i(w) w∈Rdmin f(w) where f(w)=defn1i=1∑nfi(w)
假设数据分布在K个客户端,则联邦学习将每个设备的平均损失函数,按照设备的数据集大小进行加权平均,对上式进行改写(Fk是单个设备上所有样本的平均损失函数,nk是第k个设备的样本数量,pk是第k个设备的样本集合,n为系统所有设备的样本数量之和):
f ( w ) = ∑ k = 1 K n k n F k ( w ) where F k ( w ) = 1 n k ∑ i ∈ P k f i ( w ) f(w)=\sum_{k=1}^{K} \frac{n_k}{n}F_k(w)\ \texttt{where} \ F_k(w)=\frac{1}{n_k}\sum_{i\in \mathcal{P}_k}f_i(w) f(w)=k=1∑KnnkFk(w) where Fk(w)=nk1i∈Pk∑fi(w)
如果划分Dk是所有用户数据的随机取样(符合分布式优化问题的独立同分布假设),则目标函数f(w)就等价于损失函数关于Dk的期望:
E P k [ F k ( w ) ] = f ( w ) \mathbb{E}_{\mathcal{P}_k}[F_k(w)]=f(w) EPk[Fk(w)]=f(w)
【通信成本与计算成本】
在数据中心优化问题中,通信成本相对较小,而计算成本占主导地位(可使用GPU来降低这些成本);而在联邦优化中:
- 通信成本占主导地位(通常会受到1MB/s或更小的上传带宽限制;客户通常只会在充电,插入电源和不计量的Wi-Fi连接时自愿参与优化;希望每个客户每天只参加少量的更新轮)
- 且计算成本相对较小(任何单个设备上的数据集都比总数据集的规模小;现代智能手机具有相对较快的处理器)
因此,尽量使用额外的计算来减少训练模型所需的通信次数。
两种方法来添加计算量:
- 提高并行性:在每个通信轮之间使用更多的客户端独立工作;
- 增加每个客户端的计算量: 与执行像梯度计算那样的简单计算不同,每个客户端在每个通信轮之间执行更复杂的计算。
研究两种方法发现,实现加速主要是由于在每个客户端上增加了更多的计算。
4.相关工作
McDonald等人研究了通过迭代平均本地训练模型,分布式训练感知机(2010);Povey等人研究了用于语音识别DNN(2015);张等研究了一种具有 “软”平均的异步方法(2015)。
这些工作仅考虑集群/数据中心设置(最多16个工作人员,基于快速网络的挂钟时间),不考虑不平衡且非IID的数据集。
Neverova等人讨论了将敏感用户数据保存在设备上的优点(2016);Shokri和Shmatikov的工作有多种联系:专注于训练深层网络,强调隐私的重要性,并通过在每一轮通信中仅共享一部分参数来解决通信成本(2015)。
没有考虑不平衡和非IID数据,因此实证评估是有限的。
在凸设置中,分布式优化和估计问题受到了极大关注(Balcan等,2012; Fercoq等,2014; Shamir和Srebro,2014),一些算法专门针对通信效率(Shamir et al。,2013; Yang,2013; Ma et al。,2015; Zhang and Xiao,2015)。
需满足凸性假设;且通常要求客户端数量<客户端的平均数据量,数据以IID方式分布在客户端之间,并且每个节点客户端都具有相同的数据点数量。而联邦优化的设置不符合这些假设。
SGD的异步分布式形式也已用于训练神经网络,例如Dean等(2012)。
这些方法在联邦学习中需要进行大量更新。
分布式共识算法放松了数据的IID假设(2014)。
仍不适合在很多客户端上进行通信优化。
最终考虑简单一次平均(simple one-shot averaging),每个客户端训练将其本地数据的损失降到最低(可能是正则化的)的模型,然后将这些模型取平均值以生成最终的全局模型。
这种方法已经在带有IID数据的凸情况下进行了广泛的研究,在最坏的情况下,生成的全局模型并不比在单个客户端上训练模型更好(Zhang等人,2012;
Arjevani和Shamir,2015; Zinkevich等,2010)。
二、FedAvg算法
从SGD开始构建用于联邦优化的算法,随机梯度下降的重要性:
- 深度学习的最新成功应用几乎都依赖于随机梯度下降(SGD) 的变体进行优化;
- 实际上,许多进展可以理解为通过调整模型的结构(或者损失函数),使其更易于使用简单的gradient-based methods进行优化(Goodfellow等,2016)。
基线算法:FederatedSGD(FedSGD)
- SGD可以直接应用于联邦优化,即每轮在随机选择的客户端上进行一次梯度计算。计算有效,但需要进行大量训练才能生成好的模型。
- 将大批量同步SGD(实验表明其在数据中心设置中是最先进的,优于异步方法)应用于联邦学习,需要在每一轮中选择C个客户端。
设置C=1,固定学习率为η,下面两者等价(FedSGD->FedAvg):
-
第k个客户端计算梯度 g k = ∇ F k ( ω ) g_{k}=\nabla F_{k}(\omega) gk=∇Fk(ω),
中心服务器聚合梯度并更新 w t + 1 ← w t − η ∑ k = 1 K n k n g k w_{t+1} \leftarrow w_{t}-\eta \sum_{k=1}^{K} \frac{n_{k}}{n} g_{k} wt+1←wt−η∑k=1Knnkgk;
-
第k个客户端计算梯度 g k = ∇ F k ( ω ) g_{k}=\nabla F_{k}(\omega) gk=∇Fk(ω),并更新参数 w t + 1 k ← w t − η g k w_{t+1}^{k} \leftarrow w_{t}-\eta g_{k} wt+1k←wt−ηgk
中心服务器聚合梯度 w t + 1 ← ∑ k = 1 K n k n w t + 1 k w_{t+1} \leftarrow \sum_{k=1}^{K} \frac{n_{k}}{n} w_{t+1}^{k} wt+1←∑k=1Knnkwt+1k
| worker节点(第i个) | server节点 | |
|---|---|---|
| FedSGD | 从server接收模型参数w; 用w和本地数据计算梯度 g k g_k gk; 发送 g k g_k gk给server |
从m个workers接收梯度 g 1 , . . . , g m g_1,...,g_m g1,...,gm; 计算 g = g 1 + . . . + g m g=g_1+...+g_m g=g1+...+gm; 更新模型参数 w ← w − α ⋅ g w\leftarrow w-\alpha·g w←w−α⋅g |
| FedAvg | 从server接收模型参数w; 重复步骤:用w和本地数据计算梯度 g g g, 并完成本地更新 w ← w − α ⋅ g w\leftarrow w-\alpha·g w←w−α⋅g |
从m个workers接收参数 w ~ 1 , . . . , w ~ m \widetilde{w}_1,...,\widetilde{w}_m w 1,...,w m; 更新模型参数 w ← 1 m ( w ~ 1 + . . . + w ~ m ) w\leftarrow \frac{1}{m}(\widetilde{w}_1+...+\widetilde{w}_m) w←m1(w 1+...+w m) |
C=E=1 ,B=∞时,FedAvg等价于FedSGD:每次采用client的所有数据集进行训练,本地训练次数为1,然后进行聚合
- C:每次参与联邦聚合的clients数量占client总数的比例(C=1 代表所有成员参与聚合)
- B:client的本地的训练的batchsize,B=无穷大代表batchsize是整个本地数据集
- E:两次联邦训练之间的本地训练的次数
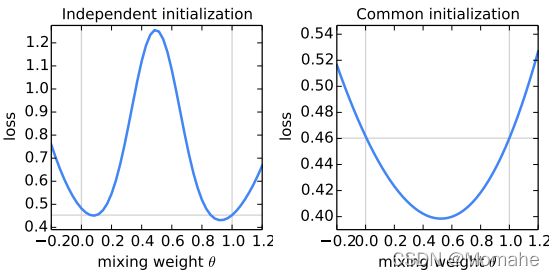
对于一般的非凸目标函数,参数空间中的平均模型可能会产生任意不好的模型结果。 按照Goodfellow等人(2015年)的方法 ,当平均两个从不同初始条件训练的MNIST数字识别模型时,可看到这种不良结果(图左);而从相同的随机初始化开始两个模型,然后在不同的数据子集上对每个模型进行独立训练,平均效果很好(图右)。由此应用于FedAvg,客户端从中心服务器加载相同的初始化模型,中心服务器采用加权平均方法聚合客户端的训练模型。
FedAvg算法步骤:
- 服务器初始化训练模型 w 0 w_0 w0;
- 进行第t轮模型融合,服务器从所有客户端中随机选取 S t S_t St 个客户端,将模型广播给被选择的客户端;
- 被选择的客户端将接受到的模型作为初始化模型,利用本地数据进行训练,然后将新模型参数 w t + 1 k w^k_{t+1} wt+1k 上传给服务器;
- 服务器聚合收到的模型,对k个模型取平均得到 w t + 1 w_{t+1} wt+1;
- 依次往复,进行下一轮模型融合;
三、实验结果
1.数据集和对应模型
MINIST digit recognition(图像分类):
- 两种数据划分(IID & non-IID)
- IID:将数据打乱,100个clients,平均每个clients有600个样本;
- non-IID:按照数字标签(0-9)对数据进行排序,然后划分为200个大小为300的“片段”,然后给100个clients分配2个“片段”(每人600条数据,且最多有两个数字标签的数据)
- 两种模型:simple multilayer-perceptron;CNN
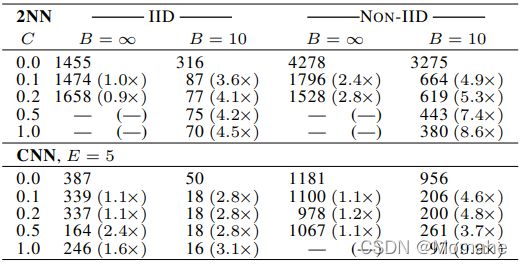
对于IID和non-IID的数据,提高E和B都能减少通信轮数,并且对于不同pair的手写数据集,模型平均竟然有一些效果,说明了方法具有鲁棒性。
Language Modeling for Works of Shakespeare
- 两种数据划分:
- 为每个剧中的每个角色构造一个client数据集(至少两行),共1146个clients;每个client有80%的训练行数据和20%的测试行数据(训练集中有3,564,579个字符,测试集中有870,014个字符),该数据是不平衡的,许多角色只有几行,而有些角色有很多行;每个剧本按时间顺序将行分为训练集与测试集,而不是随机划分样本;
- 使用相同的训练/测试拆分,构造平衡的IID版本的数据集,也有1146个客户端。
- 模型为堆叠的字符级LSTM语言模型(读取一行中的每个字符后,预测下一个字符)
莎士比亚的不平衡和非IID分布数据(按角色扮演)更能代表实际应用中的数据分布,训练更加容易(加速95倍,而平衡IID数据则为13倍)。推测这主要是由于某些角色具有相对较大的本地数据集,使得增加本地训练特别有价值。
CIFAR-10 dataset(进一步验证FedAvg的效果)
- 均衡的IID数据:将数据(由具有三个RGB通道的10类32x32图像组成)划分为100个clients,每个client包含500个训练样本和100个测试样本。
- 模型架构取自TensorFlow教程,包括2个卷积层、2个全连接层和1个线性转换层生成logit(共约106个参数)
对于CIFAR数据集,最先进的方法已达到96.5%的测试准确度; 但目标是评估优化方法,而不是在此任务上获得最佳的准确性,所以使用标准的模型架构即可。
大规模LSTM实验(探索FedAvg和FedSGD在各种learning rate下的效果)
- 按作者对大型社交网络的1000万条公开帖子进行分组(总共有50多万客户),将每个客户数据集限制为最多5000个单词,并在来自不同作者的1e5篇文章的测试集上报告准确性(在10000个可能性中,对下一个单词的正确预测概率最高的数据的一部分)。
- 模型为基于10,000个单词词汇表的256个节点LSTM
实验需要大量的计算资源,因此没有彻底探讨超参数。所有运行都训练200个clients/轮,FedAvg使用B = 8,E =5
2.分析超参数C、E、B对实验结果的影响,以便后续研究(达到指定准确度所需的通信轮数):
-
增加每个客户端的计算量(C=0.1;E、B)
每个客户端每回合的预期更新次数: u = ( E [ n k ] / B ) E = n E / ( K B ) u=\left(\mathbb{E}\left[n_{k}\right] / B\right) E=n E /(K B) u=(E[nk]/B)E=nE/(KB)

下图表明每轮添加更多本地SGD更新可以大大降低通信成本,上表量化了这些加速。

3.三个模型总结分析
FedAvg收敛到比基准FedSGD模型更高的测试集准确性水平(即使超出了绘制范围,这种趋势仍继续)。例如,对于CNN,B =∞,E = 1 FedSGD模型最终在1200轮后达到了99.22%的准确度(并且在6000轮之后并没有进一步改善);而B = 10,E = 20的FedAvg模型达到了300轮后达到99.44%。因此推测,除了降低通信成本外,模型平均还产生了与dropout正则化相似的优化效果。关注泛化性能,FedAvg在优化训练损失方面也很有效。
能否让客户端一直优化下去?
当前模型参数仅通过初始化影响每个Client Update中执行的优化。 当E→∞时,至少对于凸问题,并且无论初始化如何,都将达到全局最小值;对于非凸问题,只要初始化是在同一个“盆地”中,算法也会收敛到相同的局部最小值。可以说,虽然一轮平均可以产生一个合理的模型,但是额外的几轮交流(和平均)不会产生进一步的改进。
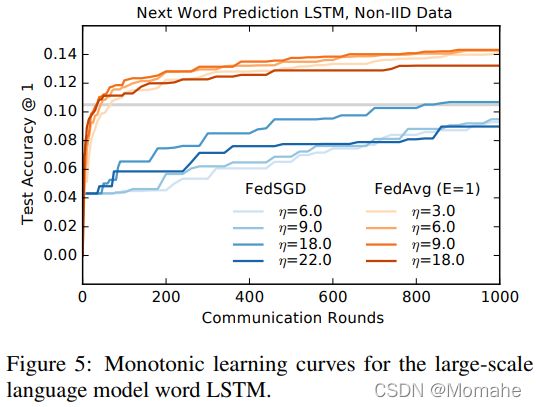
下图显示了训练中E的设置对莎士比亚LSTM的影响,可以看到E的增大,不一定带来收敛速度的明显下降。

下表给出了在CIFAR-10数据集上,Baseline SGD,FedSGD和FedAvg达到三项不同精度目标所需的轮数。

对于所有算法,除了初始learning-rate外,还调整了learning-rate decay,下图给出了FedAvg与FedSGD的学习率曲线,可看出FedAVG相对于FedSGD在相同效果情况下,通信成本大大降低:
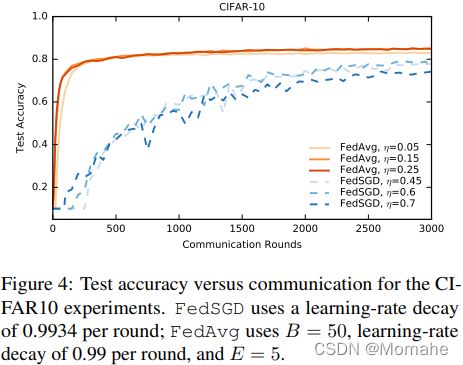
下图使用大规模LSTM实验,显示了最佳学习率的单调学习曲线。 η= 0.4的FedSGD需要310轮才能达到8.1%的准确度,而η= 18.0的FedAvg仅在20轮就达到了8.5%的准确性(比FedSGD少15倍):
四、结论和未来工作
优点:用于解决FedSGD模型融合耗时过长问题,通过增加节点本地运算量,减少了通信量,提升训练效率。
缺点:各个客户端公用一个融合模型,对于非独立同分布数据,可能无法满足各个客户端需求。