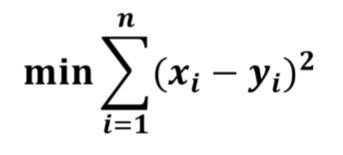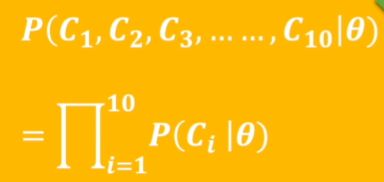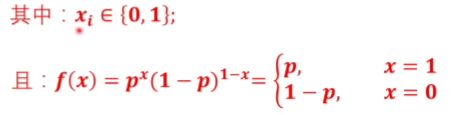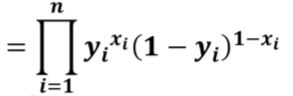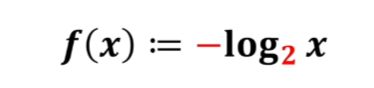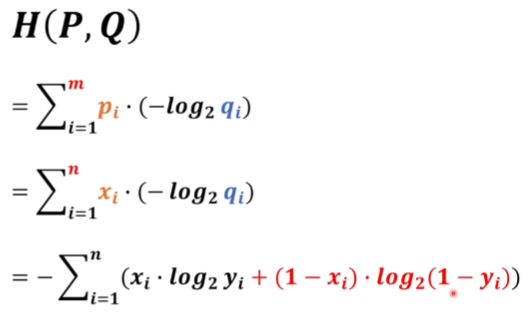由损失函数设计原理,重理解交叉熵推导
主要讨论最小二乘,极大似然估计,交叉熵
思路来源:“损失函数”是如何设计出来的?直观理解“最小二乘法”和“极大似然估计法”_哔哩哔哩_bilibili
目录
最小二乘
极大似然估计
由概率分布推预测结果:
由结果推概率分布:
交叉熵
信息量
熵
KL散度
最小二乘
最直观寻找两个值之间差距大小,直接相减的绝对值,为了方便求导,加个平方
最小二乘名字的理解:平方就是乘两次,找这个二乘式的最小值
其实就是在说均方差损失,连加对应过来就是每一组训练数据,在计算损失的时候一个一个的计算或者按照一个batch计算,也是需要Loss_function最小
极大似然估计
由概率分布推预测结果:
如果我们已知抛硬币 为正的概率和为反的概率都为0.5,即x和p服从如下概率分布时,可以推测抛10次硬币的结果五个正、五个反。
这个是基于当前概率分布的理论预测值
由结果推概率分布:
假设结果已经发生,抛硬币十次的结果如下图
当结果为下方图一所示时,举例左边三种概率分布,计算其发生的可能性
也就是在![]() 这个概率分布下,发生每次事件的概率:
这个概率分布下,发生每次事件的概率:
可以直观感受到概率分布为0.7:0.3时投出7正3负的可能性最大
极大似然估计:由于是从结果反推的概率分布,所以这个分布就叫做似然值,而使得结果最大的这一组似然值可以认为是估计得最接近真实值的一组概率分布,所以叫极大似然估计。
带入分类问题中,w,b视为概率分布,x为标签值,y为通过w,b这个分布计算出的预测值
因为分类只有0,1两种情况,所以符合伯努利分布
第1类时预测值为p,第0类预测值为1-p
转化到分类问题中就是第1类时预测值为y,第0类预测值为1-y
所以一式 等于:
由于连乘计算量太大,所以加log换加法
此时算的是使之概率最大的似然,加个负号转换为最小问题,就跟交叉熵损失基本一致了
交叉熵
信息量
信息量:衡量一个事件从不确定到确定的难度有多大
一个信息的信息量大小不是由你知不知道这个信息决定的,比如吴恩达昨天吃了汉堡,确实是一个未知的信息,但是这个信息也确实没啥作用。
信息量看的是一个信息能带来多少确定性
假设每个队实力相同,那么阿根廷夺冠的概率就是八分之一
那如果一个信息说阿根廷夺冠了,这个信息量就很高,或者阿根廷进决赛了,也消除了一部分不确定性,也是有信息量的,但是没夺冠高
要将P(夺冠)=P(进决赛)*P(赢决赛)通过一个f转换成加法,自然想到log,概率越小的事件发生信息量越大,log是单调增的,所以加一个符号,底数任取不影响走向即可
熵
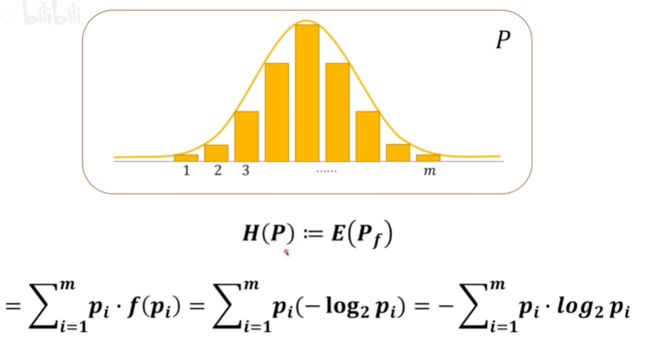
熵:衡量一个系统的所有时间从不确定到确定的难度
下述两场球赛视为两个系统,我们需要设计一种计算模式,使得哪个系统从不确定到确定的难度越大,那个系统的熵就要越大
按照上述定于计算每队赢球的信息量,但是由于每个系统只有一个队赢,不会两个队赢球同时发生,所以贡献的信息量要乘自己的概率再加起来
可以看出来第一个系统的熵明显高于第二个系统,就将这种对系统贡献的信息量定义为熵
图p表示某种概率分布下,熵的定义如下
KL散度
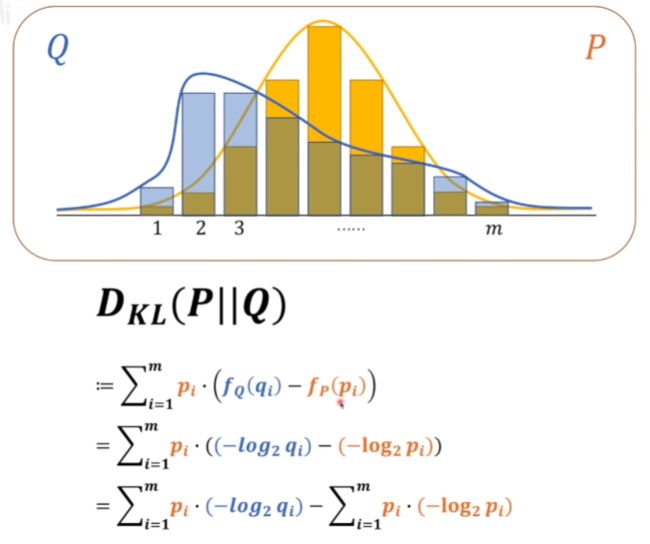
计算两个分布的差别
fp fq代表两个概率分布系统的信息量
计算散度时,P||Q 和Q||P是不等的
上图为以P为基准计算与Q的相差程度,用p的概率乘信息量的差再求期望(均值)
p,q信息量相等的话KL散度就为零,所以不等于0就代表两个概率分布有差别
展开后的减号右边部分就是系统p的熵,熵肯定都是大于零的,两个大于零的数相减不确定,通过下面这个结论可以确定此处相减大于零
KL散度越大差距越大,而减号左边值越小,KL散度就越小,而左边这一部分就是p,q的交叉熵
所以求KL散度最小就转换为求交叉熵最小
此处的x表示输入图像的标签,y表示预测值
q表示的是有多像猫,当x为1时求有多像猫的概率,x为0时求有多不像猫的概率,所以最后构造成下图形式