cv2.resize()原理详解

以下使用python语言，使用opencv库，解释最近邻插值法和双线性插值法的原理，并通过python代码复现。

文章借鉴：https://blog.csdn.net/jningwei/article/details/78822026

以及           https://www.cnblogs.com/lfri/p/10596530.html

 

目录

1、cv2.resize函数说明

2、最近邻插值与双线性插值

 3、源代码复现

效果对比：

---

---

1、cv2.resize函数说明

    resize是opencv库中的一个函数，主要起到对图片进行缩放的作用。

   example: 以下代码就可以将原图片转化为宽和长分别为300，300的图片。width和height可以自己任意指定，不论大小。

import cv2 as cv

width = 300
height = 300
img = cv.imread('图片所在路径')
#例如cv.imread("test/1.jpg")

img = cv.resize(img,(width,height))
# 默认使用双线性插值法

cv.imshow("img",img)
cv.waitKey(0)
cv.destroyAllWindows()

 

  参数说明：

resize(InputArray src, OutputArray dst, Size dsize, 
        double fx=0, double fy=0, int interpolation=INTER_LINEAR )

InputArray src ：输入，原图像，即待改变大小的图像；
OutputArray dst： 输出，改变后的图像。这个图像和原图像具有相同的内容，只是大小和原图像不一样而已；
dsize：输出图像的大小，如上面例子（300，300）。

其中，fx和fy就是下面要说的两个参数，是图像width方向和height方向的缩放比例。
fx：width方向的缩放比例
fy：height方向的缩放比例

如果fx=0.3，fy=0.7，则将原图片的x轴缩小为原来的0.3倍，将y轴缩小为原来的0.7倍，效果如下：

interpolation（插值）：这个是指定插值的方式，图像缩放之后，肯定像素要进行重新计算的，就靠这个参数来指定重新计算像素的方式，有以下几种：
INTER_NEAREST - 最邻近插值
INTER_LINEAR - 双线性插值，如果最后一个参数你不指定，默认使用这种方法
INTER_CUBIC - 4x4像素邻域内的双立方插值
INTER_LANCZOS4 - 8x8像素邻域内的Lanczos插值

 

2、最近邻插值与双线性插值

（1）INTER_NEAREST | 最近邻插值

opencv使用：python只需要    img = cv.resize(img,(width,height),interpolation=cv.INTER_NEAREST) 一行代码即可

在一维空间中，最近点插值就相当于四舍五入取整。在二维图像中，像素点的坐标都是整数，该方法就是选取离目标点最近的点。

会在一定程度上损失 空间对称性（Alignment）

1 2 3                
4 5 6  ----------->> 将3*3的图片转换为5*5
7 8 9             

1、使用最近邻插值法，令原图片为n*n，目标图片为m*m,图片从0开始数
则目标图片（i，j）位置的像素值为（n/m）*i，（n/m）*j这两个数四舍五入取整对应的原图片的像素

如目标图片（2，2）位置的像素为（3/5）*2，（3/5）*2，四舍五入取整也就分别是（1，1），而这对应原图片的像素值为5，即目标图片（2，2）的像素值为5

[[1 2 2 3 3]
 [4 5 5 6 6]
 [4 5 5 6 6]
 [7 8 8 9 9]
 [7 8 8 9 9]]

（2）INTER_LINEAR | 双线性插值（默认设置）

opencv使用：python只需要    img = cv.resize(img,(width,height),interpolation=cv.INTER_LINEAR) 一行代码即可

  在两个方向分别进行一次线性插值。

   在图像处理的时候，我们先根据

srcX = dstX* (srcWidth/dstWidth)
srcY = dstY * (srcHeight/dstHeight)

  来计算目标像素在源图像中的位置，这里计算的srcX和srcY一般都是浮点数，比如 f（1.2, 3.4）这个像素点是虚拟存在的，先找到与它临近的四个实际存在的像素点

（1，3） （2，3）
（1，4） （2，4）

   写成 f(i+u,j+v)的形式，则 u=0.2,v=0.4, i=1, j=3。

f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1) 

  保证了 空间对称性

 

 3、源代码复现

1、最近邻插值

# 将最近邻插值法源代码复现
import cv2 as cv
import numpy as np
height = 250
width = 250
dst = np.zeros([width,height,3],dtype='uint8')
img = cv.imread("test/1.jpg")
for c in range(3):
    for i in range(width):
        for j in range(height):
            x = (img.shape[0]/width)*i
            y = (img.shape[1]/height)*j
            dst[i,j,c] = img[round(x),round(y),c]
#             print (dst[i,j,c])
print (type(dst))
print (type(img))
cv.imshow("img",img)
cv.waitKey(0)
cv.imshow("dst",dst)
cv.waitKey(0)
cv.destroyAllWindows()

效果对比：

2、双线性插值（默认）

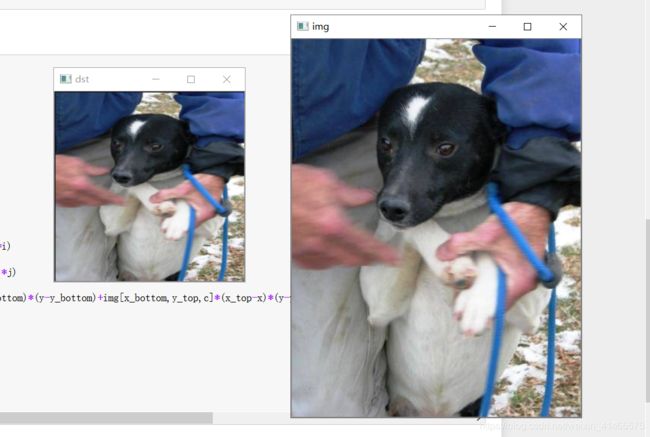
# 将双线性插值法源代码复现
import cv2 as cv
import numpy as np
import math
height = 250
width = 250
dst = np.zeros([width,height,3],dtype='uint8')
img = cv.imread("test/1.jpg")
for c in range(3):
    for i in range(width):
        for j in range(height):
            x = (img.shape[0]/width)*i
            y = (img.shape[1]/height)*j
            
            x_top = math.ceil((img.shape[0]/width)*i)
            x_bottom = int((img.shape[0]/width)*i)
            y_top = math.ceil((img.shape[1]/height)*j)
            y_bottom = int((img.shape[1]/height)*j)
            dst[i,j,c] = img[x_top,y_top,c]*(x-x_bottom)*(y-y_bottom)+img[x_bottom,y_top,c]*(x_top-x)*(y-y_bottom)+img[x_bottom,y_bottom,c]*(x_top-x)*(y_top-y)+img[x_top,y_bottom,c]*(x-x_bottom)*(y_top-y)

print (type(dst))
print (type(img))
cv.imshow("img",img)
cv.waitKey(0)
cv.imshow("dst",dst)
cv.waitKey(0)
cv.destroyAllWindows()

效果对比： 

可以看出，上述两种不同的插值方式，最终生成的图片差别并不明显