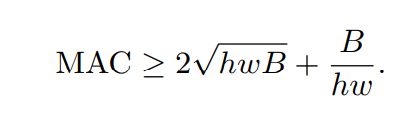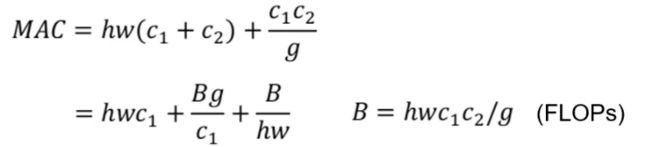ShuffleNetV1详解、ShuffleNetV2对计算复杂度的优化做了非常详细的分析
ShuffleNetV1
提出了channel shuffle思想
作者给出的解释是:
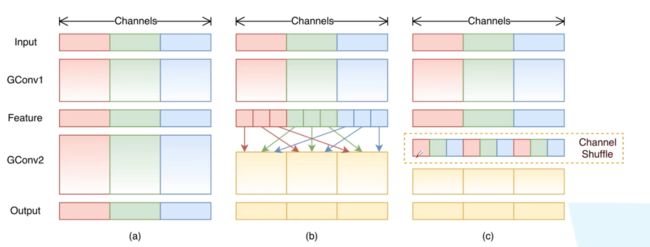
对于组卷积而言,每个通道之间没有数据交流(图a)
而shuffleNet使用channel shuffle操作,将组卷积分出的g个组再划分g次,成g个小组
每个大组的第i个小组组合在一起形成新的组,再进行卷积。
ShuffleNetV1的block
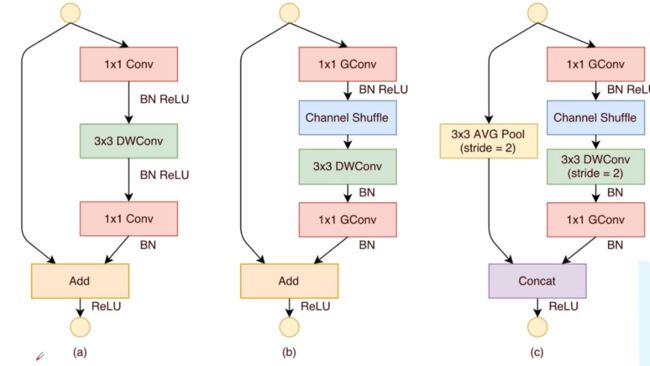
(a)为残差结构
(b)为stride=1时,shuffleNet的block
(c)为stride=2时,shuffleNet的block,跳跃连接用的池化,而不是1*1卷积
channel shuffle实现
定义channel_shuffle函数来实现该操作
传入要操作的tensor矩阵 x 和要划分成多少组 g
传入数据x的size排列顺序为 batch_size,channels,herght,width
用x的channels除以g获取划分后的channel大小 c2 = c1/g
原本是b*c1*h*w
转换为b*g*c2*h*w
def channel_shuffle(x: Tensor, groups: int) -> Tensor: batch_size, channels, height, width = x.size() channels_per_group = channels // groups # reshape # [batch_size, channels, height, width] -> [batch_size, groups, channels_per_group, height, width] x = x.view(batch_size, groups, channels_per_group, height, width) x = torch.transpose(x, 1, 2).contiguous() # flatten x = x.view(batch_size, -1, height, width) return x
对size操作的理解和验证
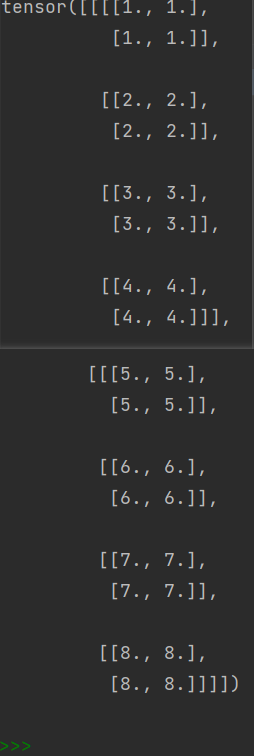
先构造一个b*c1*w*h为2*4*2*2的tensor
x = torch.FloatTensor([[[[1,1],[1,1]],[[2,2],[2,2]],[[3,3],[3,3]],[[4,4],[4,4]]],[[[5,5],[5,5]],[[6,6],[6,6]],[[7,7],[7,7]],[[8,8],[8,8]]]])
![]()
每个通道取不同的值方便验证size将那几个通道分类到一起
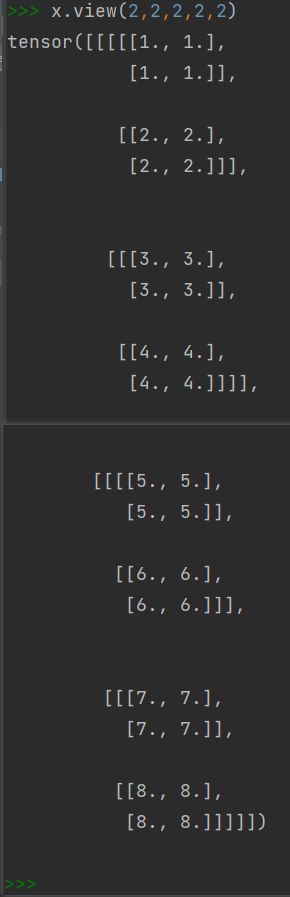
模拟g取2时,c2=c1/g=2
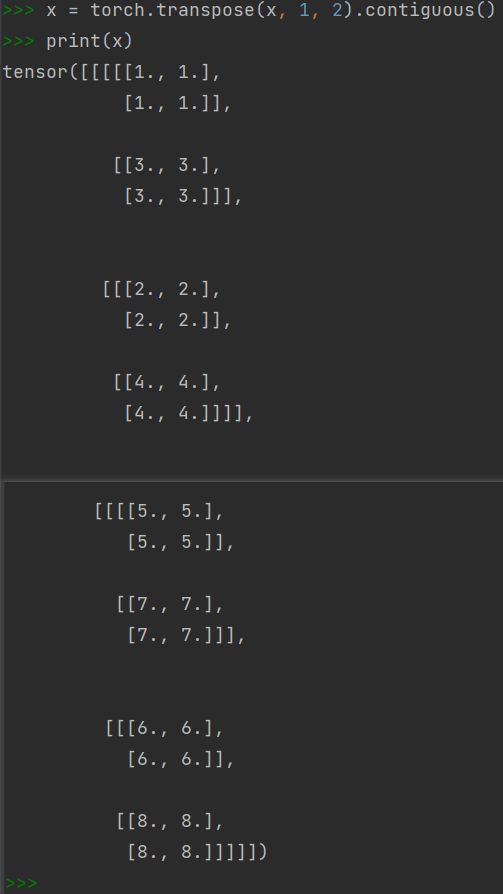
x = x.view(2,2,2,2,2)transpose做的是转置操作
例如一个c*h*w为2*2*3的矩阵transpose(1,2)的结果为2*3*2,成为原矩阵的转置
x = torch.transpose(x, 1, 2).contiguous()但此处不是对高宽操作,是对g和c2操作,转置就达到了取出每组第i个通道组合在一起的效果
此处转置的理解:
效果就变为如下:
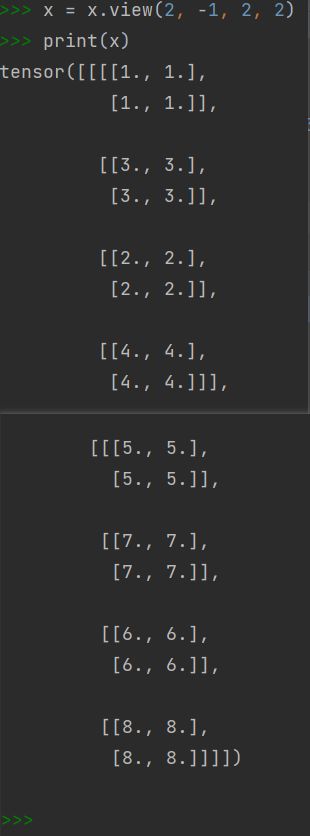
最后做一个展开
view中-1的含义是根据周围其他数值限定的形状,结合输入维度自适应-1处的大小
此处的输入是2*2*2*2*2 自适应限定了2*-1*2*2 所以输出结果将二三维合并输出,也就是形成了将两个小的组拼会一起形成一个大组的效果。
# flatten
x = x.view(batch_size, -1, height, width)浮点计算量FLOPs
对比resnet和resnext,主要减少的参数就在于
①1*1卷积换成了1*1组卷积②将3*3组卷积换成了逐通道卷积
两个1*1卷积换组卷积计算次数除以g
3*3卷积换成逐通道卷积计算量除以通道数m
总结
V1的内容很少,感觉更像是ResNeXt的一次升级
①在ResNeXt的基础上改动了一下组卷积构成channel shuffle
②在残差结构上改动了1*1卷积为组卷积,3*3卷积改为逐通道卷积,也就是改为组卷积的极限情况
跳跃连接用池化替换1*1卷积
ShuffleNetV2
ShuffleNetV2论文中对计算复杂度以及优化做了非常深度的分析
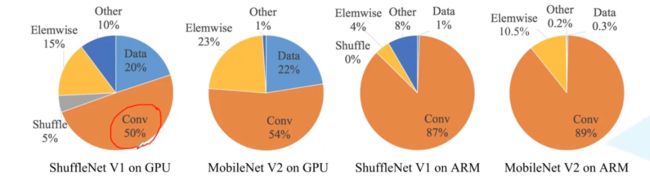
在评价计算复杂度的时候,其实看的时整体运行时间,而不是单看模型的理论计算量FLOPs
例如MAC(memory acces cost)内存访问往往会占用大量时间,例如大量的打印操作,或者使用SummerWriter往tensorboard中写入数据都会使时间花在io操作,以及数据的读取,都会使得计算卡在cpu中。
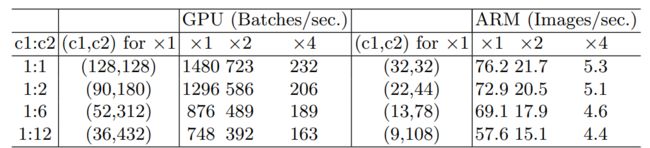
原文给出了在GPU中和在基于ARM的cpu中的时间占比
提出了四个结论
G1) 输出通道与输入通道相等时,MAC消耗最小
G1) Equal channel width minimizes memory access cost (MAC).
证明:
推导是当卷积为1*1时,浮点计算量B=h*w*c1*c2(高 宽 输入通道 输出通道)
MAC=h*w*(c1+c2)+c1*c1 (h w c1是输入的计算量,
h w c2是输出的FLOPs,
c1*c2是卷积核。1*1*c1大小 c2个卷积核)
将MAC等式套入均值不等式
该均值不等式取等的条件是 c1=c2,所以输入与输出通道相等时取得MAC的最小值
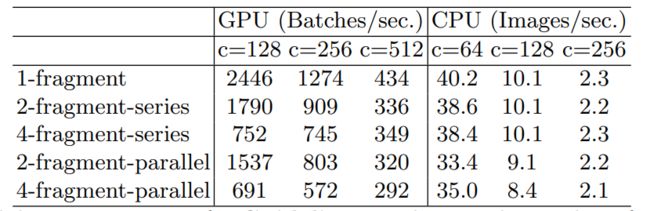
G2)当组卷积的组增大时,MAC也会变大
G2) Excessive group convolution increases MAC.
有一个大前提是FLOPs不变的情况下满足这个结论,也就是说当g增大后c是需要增大才能保持B不变的
这里你可能会认为,g增大真正的影响是由c的增加带来的
但是此处我们计算的是读取一组数据花的时间,而不是计算时间,当B不变时读入数据的总FLOPs是不变的,也就是cpu需要读取的总量不变,所以任然是控制了变量的
实验结果数据:
G3)网络的碎片化程度越高,速度越慢
G3) Network fragmentation reduces degree of parallelism.
碎片化可以理解为网络的分支的多少,串联并联都算分支
虽然这种零散的结构已被证明对准确性有利,但它可能会降低效率,因为它对具有强大并行能力的设备不友好。它还引入了额外的开销,如内核启动和同步。启动和同步。
series串行实验结果,parallel并行实验结果
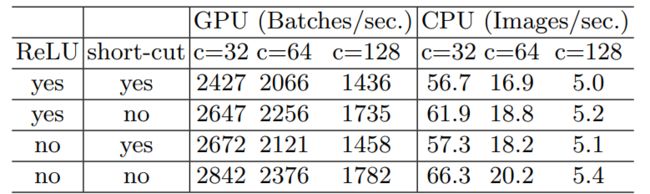
G4) Element-wise operations are non-negligible.
Element-wise主要指relu或者加减之类的,表达的就是将relu或者short_cut连接加在合适的位置,不要随意的堆叠在无用的地方徒增计算成本
V2对网络结构的优化
有了上述四条理论后,从(a)(b)优化成(c)(d)
(c)对应sride=1 (d)对应sride=2