【数据结构】线性表的应用:稀疏一元多项式运算器
***************************
本文作者科大MF22某班Noah懒羊羊同学,为大家提供一个作业思路,请勿直接copy!!!一起进步学习~
*****************************
目录
1.问题的描述
1.1基本功能
1.2健壮性
1.3 规范性
2.算法的描述
2.1数据结构的描述
2.2程序结构的描述
3.调试分析
4.算法的时空分析
5.测试结果及分析
6.实验体会和收获
代码
Noah_exp1.h
Main.cpp
1.问题的描述
1.1基本功能
- 使用所学线性表知识构建一元多项式数据结构,并且实现创建、显示、求和、微分和不定积分等功能。
- 关于创建和显示功能,输入格式不作要求,输出形式如:X^3–X^2+2X-2。
- 关于求和功能,要求按照先使用创建功能创建两个多项式,然后进行求和并输出(屏幕打印),例如输入X3+3X2+2X+6和X3-X2+2X-2,输出为2X3+2X2+4X+4。
- 关于微分功能,要求先输入一个多项式,然后对其求N阶微分,例如N=1时:X3+3X2+2X+6→3X2+6X+2,N=2时:X3+3X2+2X+6→6X+6。
- 关于求不定积分功能,要求首先输入一个多项式,然后求其不定积分,例如
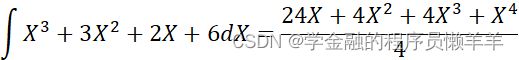
- 此外,要求整个程序需搭建出良好的人机交互模式,有菜单界面和各个功能界面,并且界面切换逻辑要正确。
1.2健壮性
- 输入X3-X2+2X-2时,按X3、-X2、+2X、-2顺序输入 和 按-2、X3、-X2、+2X顺序输入时,结果显示的是否相同。
- 求和:会把系数为0项消除:(X3+3X2+2X+6) + (X3-3X2+2X+6)=2X3+4X+12。
- 微分 N=4 :X3+3X2+2X+6→0。
- 菜单界面和各个功能界面切换逻辑正确。
1.3 规范性
- 代码注释
- 程序模块化
- 人机交互友好
2.算法的描述
2.1数据结构的描述
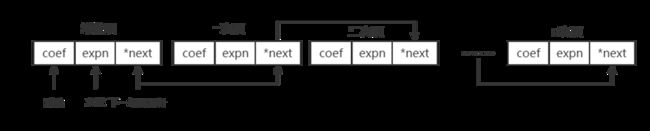
使用单链表结构来存储,结点使用结构体对多项式的每一项进行定义,每个节点中包含三个元素,分别是系数、指数和下一结点指针。数据的逻辑结构如下图所示,
在内存中,结点并不存储在相邻的存储空间,而是通过每个结点中的*next指针来访问下一结点,通过头结点即可找到所有结点。
主要变量说明:
| 变量 |
类型 |
说明 |
| polynomial_Node |
结构体 |
多项式中的单项结点结构体 |
| *polylist |
机构体指针 |
用于访问结构体,存储结构体内存位置 |
| coef |
float |
polynomial_Node中的元素之一,单项式中的系数 |
| expn |
int |
polynomial_Node中的元素之一,单项式中的指数 |
| *next |
结构体指针 |
polynomial_Node中的元素之一,用于访问结构体,存储结构体内存位置 |
| pre_node |
结构体指针 |
在多个重要函数中出现,用于构建多项式数据结构时,暂存前一节点的指针 |
| result / result_return |
结构体指针 |
在多个重要函数中作为参数出现,一般作为函数的出口,存储函数操作后的输出结果 |
2.2程序结构的描述
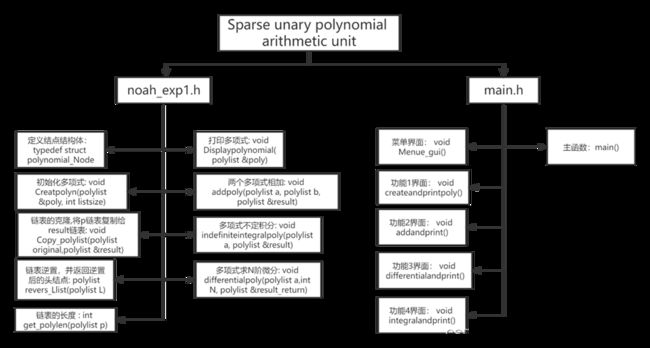
程序主要包含noah_exp1.h头文件和main.cpp主文件,其中noah_exp1.h文件为实现多项式数据结构的代码集合,main.cpp中主要实现菜单和功能界面的交互以及头文件中函数的调用。其具体结构如下,
noah_exp1.h中模块具体说明:
(1)typedef struct polynomial_Node{
/***********************
Name: polynomial_Node; *polylist
Description: 多项式结点的结构体定义
Input Parameters: -
Output Parameters: -
Return: -
Supplement: -
***********************/
(2)void Creatpolyn(polylist &poly, int listsize){
/***********************
Name: Creatpolyn()
Description: 输入listsize+1项的系数和指数,建立表示多项式的有序链表
Input Parameters: -poly, 所需初始化的链表的第一个结点(该数据结构中无头结点)
-listsize,所需初始化的链表的长度
Output Parameters: -poly,引用参数,作为出口保存了初始化后的链表的头结点
Return: -
Supplement: -该链表没有头结点
***********************/
(3)int get_polylen(polylist p){
/***********************
Name: get_polylen()
Description: 返回链表的长度(多项式的最高次幂+1)
Input Parameters: -p,所需求长度的链表的第一个结点
Output Parameters: -
Return: -len,int数据类型,为链表的长度
Supplement: -该链表没有头结点
***********************/
(4)void Copy_polylist(polylist original,polylist &result){
/***********************
Name: Copy_polylist()
Description: 链表的克隆,将p链表复制给result链表,两表的内存地址不同
Input Parameters: -original,被复制的链表的第一个结点
-result,克隆后的链表的头结点
Output Parameters: -result,引用参数,作为函数的出口保存了克隆后的链表的第一个结点
Return: -
Supplement: -该链表没有头结点
***********************/
(5)polylist revers_Llist(polylist L){
/***********************
Name: revers_Llist()
Description: 链表逆置,并返回逆置后的第一个结点
Input Parameters: -L,需要逆置的链表的第一个结点
Output Parameters: -
Return: -逆置后的第一个结点
Supplement: -该链表没有头结点
***********************/
(6)void Displaypolynomial(polylist poly){
/***********************
Name: Displaypolynomial()
Description: 以常见的格式打印多项式
Input Parameters: -poly,需要打印的链表的第一个结点
Output Parameters: -
Return: -
Supplement: -该链表没有头结点,因此第一个结点也需要打印,
输出第一项时如果系数为正则不需要输出加号,如果是常数项则不输出X,如果幂为1则不显示次幂,
系数不等于0,指数等于0时不显示X^n,
系数不等不等于0,指数等于1时不显示^n,
系数等于0时,省略该项。
***********************/
(7)void addpoly(polylist a, polylist b, polylist &result){
/***********************
Name: addpoly()
Description: 将两个多项式相加并将结果存储在result的链表中
Input Parameters: -a,需要相加的其中一个链表的第一个结点
-b,需要相加的第二个链表的第一个结点
-result,输入的空结点
Output Parameters: -result,作为函数出口,以result为第一个结点的链表保存了相加后的的多项式
Return: -
Supplement: -
***********************/
(8)void differentialpoly(polylist a,int N, polylist &result_return){
/***********************
Name: differentialpoly()
Description: 将多项式微分N阶并将结果存储在result的链表中
Input Parameters: -a,需要进行微分的多项式的第一个结点指针
-result_return,输入的空结点
Output Parameters: -result_return,作为函数出口,以result_return为第一个结点的链表保存了N阶微分后的的多项式
Return: -
Supplement: -参考了递归思路,每次进入函数N-1,当N=0时转向函数出口
***********************/
(9)void indefiniteintegralpoly(polylist a, polylist &result){
/***********************
Name: indefiniteintegralpoly()
Description: 求多项式不定积分并将结果存储在result的链表中
Input Parameters: -a,需要求不定积分的多项式的第一个结点指针
-result,输入的空结点
Output Parameters: -result,作为函数出口,以result为第一个结点的链表保存了求不定积分后的的多项式
Return: -
Supplement: -
***********************/
3.调试分析
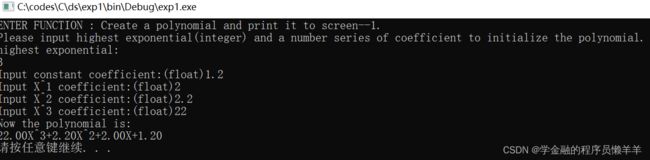
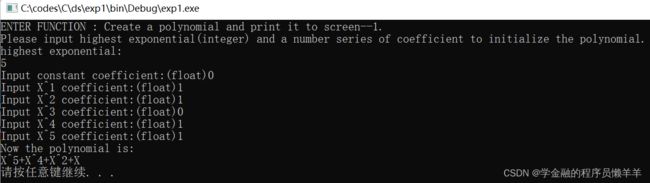
调试功能一:Create a polynomial and print it to screen
在进行初始化时首先要输入该多项式的最高次数,然后按照从低次到高次地输入系数。
测试数据选择:
- 3- 1.2, 2, 2.2 ,22
- 1-1,2
- 0-2
- 5-0, 1, 1, 0, 1, 1
问题及解决方法:
(1)float精度问题,由于判断系数的大小时(尤其是==判断)需要进行比较,但由于float数据类型的精度有问题因此使用fabs(p->coef-0.000) > FLOAT_PRECISON替代。
(2)其他打印细节问题,例如系数等于0时省略、指数为1时不显示次数,使用不同的判断语句对不同的情况进行处理。
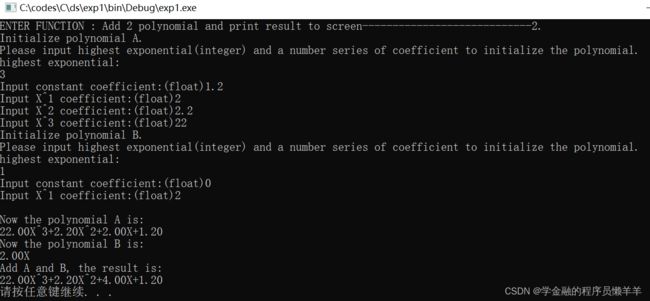
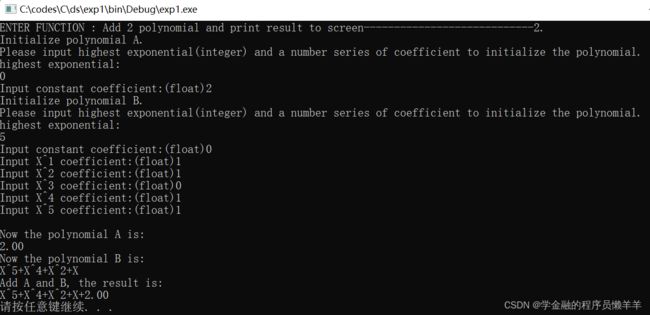
调试功能二:Add 2 polynomial and print result to screen
测试数据选择:
- 3- 1.2, 2, 2.2 ,22;1-1,2
- 0-2;5-0, 1, 1, 0, 1, 1
问题及解决方法:
无
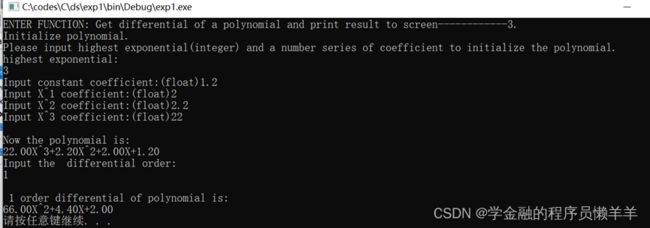
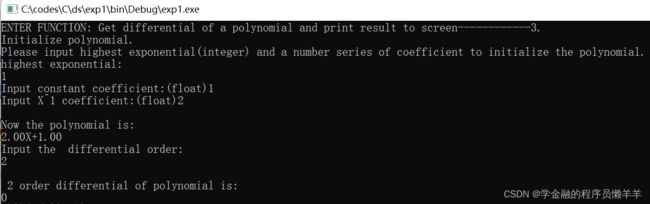
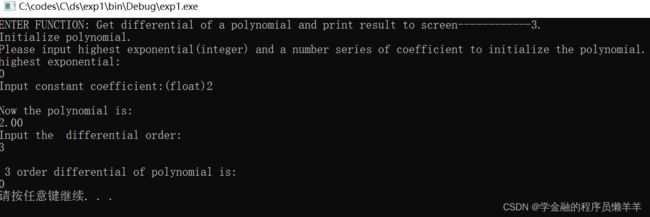
调试功能三:Get differential of a polynomial and print result to screen
测试数据选择:
- 3- 1.2, 2, 2.2 ,22;1
- 3- 1.2, 2, 2.2 ,22;2
- 1-1,2;1
- 1-1,2;2
- 0-2;1
- 0-2;2
- 5-0, 1, 1, 0, 1, 1;1
- 5-0, 1, 1, 0, 1, 1;2
问题及解决方法:
无
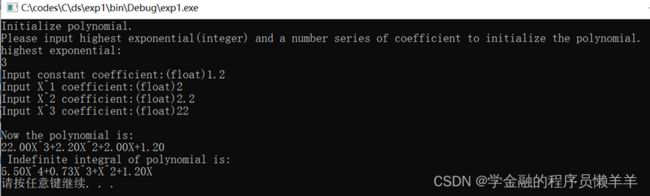
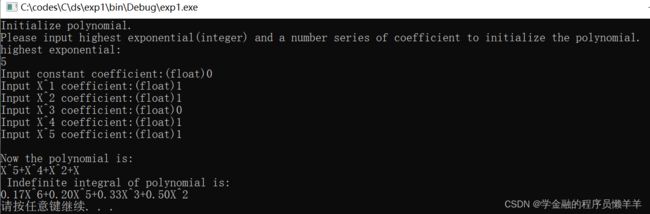
调试功能四:Get indefinite integral of a polynomial and print result to screen
测试数据选择:
- 3- 1.2, 2, 2.2 ,22
- 1-1,2
- 0-2
- 5-0, 1, 1, 0, 1, 1
问题及解决方法:
无
4.算法的时空分析
(1)void Creatpolyn(polylist &poly, int listsize)
时间复杂度:O(n)
空间复杂度:O(n)
(2)int get_polylen(polylist p)
时间复杂度:O(n)
空间复杂度:O(n)
(3)void Copy_polylist(polylist original,polylist &result)
时间复杂度:O(n)
空间复杂度:O(n)
(4)polylist revers_Llist(polylist L)
时间复杂度:O(n)
空间复杂度:O(n)
(5)void Displaypolynomial(polylist poly)
时间复杂度:O(n)
空间复杂度:O(n)
(6)void addpoly(polylist a, polylist b, polylist &result)
时间复杂度:O(n)
空间复杂度:O(n)
(6)void differentialpoly(polylist a,int N, polylist &result_return)
时间复杂度:O(n)
空间复杂度:O(n)
(6)void indefiniteintegralpoly(polylist a, polylist &result)
时间复杂度:O(n)
空间复杂度:O(n)
5.测试结果及分析
测试功能一:Create a polynomial and print it to screen
| 测试用例 |
结果 |
分析 |
| 3- 1.2, 2, 2.2 ,22 |
√,一次项不输出次幂只有 |
|
| 1-0,2 |
√,常数项为0省略输出 |
|
| 0-2 |
√,只有一项正常输出 |
|
| 5-0, 1, 1, 0, 1, 1 |
√,稀疏多项式输出正确 |
调试功能二:Add 2 polynomial and print result to screen
| 测试用例 |
结果 |
分析 |
| 3- 1.2, 2, 2.2 ,22;1-0,2 |
√,对应次幂相加正确 |
|
| 0-2;5-0, 1, 1, 0, 1, 1 |
√ |
问题及解决方法:
无
测试功能三:Get differential of a polynomial and print result to screen
| 测试用例 |
结果 |
分析 |
| 3- 1.2, 2, 2.2 ,22;1 |
√,一阶微分正常输出 |
|
| 3- 1.2, 2, 2.2 ,22;2 |
√,二阶微分正常输出 |
|
| 1-1,2;2 |
√,微分阶数大于最高次幂输出为0 |
|
| 0-2;3 |
√,微分阶数大于最高次幂输出为0 |
调试功能四:Get indefinite integral of a polynomial and print result to scree
| 测试用例 |
结果 |
分析 |
| 3- 1.2, 2, 2.2 ,22 |
√ |
|
| 1-1,2 |
||
| 5-0, 1, 1, 0, 1, 1 |
6.实验体会和收获
- 学会了灵活运用链表这种数据结构;
- 对指针、引用参数、函数返回值的认识更加深刻;
- 对递归的思想理解更加深刻,并且能够用于实战;
- 学会了如何更快地定位程序BUG并进行调试;
- 学会了如何更科学地设计测试用例来对程序进行功能测试。
代码
Noah_exp1.h
/**************************************************************************
Copyright Copyright 2022 Noah Zhan.* File Name: noah_exp1.h* Description: 实现一元稀疏多项式数据机构及相关功能** Version: V1.0* Author: Noah Zhan* Create Time: 2022-10-20
**************************************************************************/
#ifndef NOAH_EXP1_H_INCLUDED
#define NOAH_EXP1_H_INCLUDED
#define FLOAT_PRECISON 0.0000001//用于浮点数的大小比较
#include
//定义多项式结点结构体
typedef struct polynomial_Node{
/***********************
Name: polynomial_Node; *polylist
Description: 多项式结点的结构体定义
Input Parameters: -
Output Parameters: -
Return: -
Supplement: -
***********************/
float coef;
int expn;
struct polynomial_Node *next;
}polynomial_Node,*polylist;
//初始化多项式
void Creatpolyn(polylist &poly, int listsize){
/***********************
Name: Creatpolyn()
Description: 输入listsize+1项的系数和指数,建立表示多项式的有序链表
Input Parameters: -poly, 所需初始化的链表的第一个结点(该数据结构中无头结点)
-listsize,所需初始化的链表的长度
Output Parameters: -poly,引用参数,作为出口保存了初始化后的链表的头结点
Return: -
Supplement: -该链表没有头结点
***********************/
poly = (polylist)malloc(sizeof(polynomial_Node));
poly->next = nullptr;
printf("Input constant coefficient:(float)");
scanf("%f",&poly->coef);
poly->expn = 0;
//初始化剩下的listsize-1个结点
polylist pre_node = poly;
for(int i = 1; icoef);
p->next = nullptr;
p->expn = i;
pre_node->next = p;
pre_node = p;
}
}
//返回链表的长度(多项式的最高次幂+1)
int get_polylen(polylist p){
/***********************
Name: get_polylen()
Description: 返回链表的长度(多项式的最高次幂+1)
Input Parameters: -p,所需求长度的链表的第一个结点
Output Parameters: -
Return: -len,int数据类型,为链表的长度
Supplement: -该链表没有头结点
***********************/
int len = 1;
while(p->next!=nullptr){
len++;
p = p->next;
}
return len;
}
//链表的克隆,将p链表复制给result链表,两表的内存地址不同
void Copy_polylist(polylist original,polylist &result){
/***********************
Name: Copy_polylist()
Description: 链表的克隆,将p链表复制给result链表,两表的内存地址不同
Input Parameters: -original,被复制的链表的第一个结点
-result,克隆后的链表的头结点
Output Parameters: -result,引用参数,作为函数的出口保存了克隆后的链表的第一个结点
Return: -
Supplement: -该链表没有头结点
***********************/
//克隆头结点
result = (polylist)malloc(sizeof(polynomial_Node));
result->coef = original->coef;
result->expn = original->expn;
result->next = nullptr;
polylist pre_node = result;
int len = get_polylen(original);
//克隆剩下的结点
for(int i = 1; inext;
//printf("%f %d %f %d",original->coef,original->expn,original->next->coef,original->next->expn);
polylist p = (polylist)malloc(sizeof(polynomial_Node));
p->coef = original->coef;
p->expn = original->expn;
p->next = nullptr;
pre_node->next = p;
pre_node = p;
}
}
//链表逆置,并返回逆置后的第一个结点
polylist revers_Llist(polylist L){
/***********************
Name: revers_Llist()
Description: 链表逆置,并返回逆置后的第一个结点
Input Parameters: -L,需要逆置的链表的第一个结点
Output Parameters: -
Return: -逆置后的第一个结点
Supplement: -该链表没有头结点
***********************/
if(L->next==nullptr)//如果长度为1,则不必逆置
return L;
polylist p = L->next;
L->next = nullptr;
while(p){
polylist temp = p->next;
p->next = L;
L = p;
p = temp;
}
return L;
}
//打印多项式
void Displaypolynomial(polylist poly){
/***********************
Name: Displaypolynomial()
Description: 以常见的格式打印多项式
Input Parameters: -poly,需要打印的链表的第一个结点
Output Parameters: -
Return: -
Supplement: -该链表没有头结点,因此第一个结点也需要打印,
输出第一项时如果系数为正则不需要输出加号,如果是常数项则不输出X,如果幂为1则不显示次幂,
系数不等于0,指数等于0时不显示X^n,
系数不等不等于0,指数等于1时不显示^n,
系数等于0时,省略该项。
***********************/
polylist p = poly;
//输出第一项(如果系数为正则不需要输出加号,如果是常数项则不输出X,如果幂为1则不显示次幂)
if(fabs(p->coef-0.000) > FLOAT_PRECISON && p->expn==0)//系数不等于零,指数等于零时
printf("%.2f",p->coef);
else if(fabs(p->coef-0.000) > FLOAT_PRECISON && p->expn==1)//系数不等于零,指数等于1时
printf("%.2fX",p->coef);
else{
while(fabs(p->coef-0.000) < FLOAT_PRECISON){//系数等于零时,p = p->next
if(p->next==nullptr){//如果多项式只有一项且系数为0
printf("0"); return;}
p = p->next;
}
if(fabs(p->coef-1.000) < FLOAT_PRECISON && p->expn!=0)
printf("X^%d",p->expn);
else if(fabs(p->coef-(-1.000)) < FLOAT_PRECISON && p->expn!=0)
printf("-X^%d",p->expn);
else
printf("%.2fX^%d",p->coef,p->expn);
}
p = p->next;
//输出剩下的项
while(p!=nullptr){
if(fabs(p->coef-0.000) < FLOAT_PRECISON){//如果系数为0则该项不打印
p = p->next;
continue;
}
else if(p->coef<0.000 && p->expn!=0 && p->expn !=1){//系数小于零直接打印,自带减号
if(fabs(p->coef-(-1.000)) < FLOAT_PRECISON)//系数为-1
printf("-X^%d",p->expn);
else//系数不为-1
printf("%.2fX^%d",p->coef,p->expn);
}
else if(p->coef>0.000 && p->expn!=0 && p->expn !=1){ //系数大于零打印时要加“+”
if(fabs(p->coef-1.000) < FLOAT_PRECISON)//系数为1
printf("+X^%d",p->expn);
else//系数不为1
printf("+%.2fX^%d",p->coef,p->expn);
}
else if(p->expn==0){//指数为零的时候不打印X和次幂
if(p->coef>0)
printf("+%.2f",p->coef);
else if(p->coef<0)
printf("%.2f",p->coef);
}
else if(p->expn==1){//指数为1的时候不打印次幂
if(p->coef>0){
if(fabs(p->coef-1.000) < FLOAT_PRECISON)//系数为1
printf("+X");
else
printf("+%.2fX",p->coef);}
else if(p->coef<0){
if(fabs(p->coef-(-1.000)) < FLOAT_PRECISON)//系数为-1
printf("-X");
else
printf("%.2fX",p->coef);}
}
p = p->next;
}
}
//两个多项式相加
void addpoly(polylist a, polylist b, polylist &result){
/***********************
Name: addpoly()
Description: 将两个多项式相加并将结果存储在result的链表中
Input Parameters: -a,需要相加的其中一个链表的第一个结点
-b,需要相加的第二个链表的第一个结点
-result,输入的空结点
Output Parameters: -result,作为函数出口,以result为第一个结点的链表保存了相加后的的多项式
Return: -
Supplement: -
***********************/
result = (polylist)malloc(sizeof(polynomial_Node));
polylist pre_node;
int head_state = 1;//用于在生成第一个结点时的控制
if(a->expn!=0){//当a头结点次幂不为0时进行逆置操作,方便后续相加运算
a = revers_Llist(a);
}
if(b->expn!=0){//当b头结点次幂不为0时进行逆置操作,方便后续相加运算
b = revers_Llist(b);
}
while(a!=nullptr || b!=nullptr){
float coef_a,coef_b;//暂存
int expn_a,expn_b;//暂存
//计算新的coef和expt
if(a==nullptr && b != nullptr){
coef_a = 0.000;
expn_a = 0;
}
else{
coef_a = a->coef;
expn_a = a->expn;
}
if(b==nullptr && a != nullptr){
coef_b = 0.000;
expn_b = 0;
}
else{
coef_b = b->coef;
expn_b = b->expn;
}
float coef = coef_a + coef_b;
int expn = expn_a|expn_b;
//如果是头结点
if(head_state){
result->coef = coef;
result->expn = expn;
result->next = nullptr;
pre_node = result;
//printf("%f %d",result->coef,result->expn);
if(a!=nullptr)
a = a->next;
if(b!=nullptr)
b = b->next;
head_state = 0;
continue;
}
//如果不是头结点
polylist temp = (polylist)malloc(sizeof(polynomial_Node));
temp->coef = coef;
temp->expn = expn;
temp->next = nullptr;
pre_node->next = temp;
pre_node = temp;
if(a!=nullptr)
a = a->next;
if(b!=nullptr)
b = b->next;
}
result = revers_Llist(result);
}
//多项式求N阶微分
void differentialpoly(polylist a,int N, polylist &result_return){
/***********************
Name: differentialpoly()
Description: 将多项式微分N阶并将结果存储在result的链表中
Input Parameters: -a,需要进行微分的多项式的第一个结点指针
-result_return,输入的空结点
Output Parameters: -result_return,作为函数出口,以result_return为第一个结点的链表保存了N阶微分后的的多项式
Return: -
Supplement: -参考了递归思路,每次进入函数N-1,当N=0时转向函数出口
***********************/
if(get_polylen(a)<=N){//微分阶数过高时进行控制
result_return = (polylist)malloc(sizeof(polynomial_Node));
result_return->coef = 0.000;
result_return->expn = 0;
result_return->next = nullptr;
return ;
}
else if(N>0){//此时还要继续微分
polylist result;
result = (polylist)malloc(sizeof(polynomial_Node));
polylist pre_node;
int head_state = 1;//用于在生成第一个结点时的控制
while(a!=nullptr){
//如果expn为0则这项微分后不存在了,直接跳过这个node
if(a->expn==0){
a = a->next;
continue;
}
//计算微分后新的coef和expt
float coef = a->coef * a->expn;
int expn = a->expn - 1;
//如果是头结点
if(head_state){
result->coef = coef;
result->expn = expn;
result->next = nullptr;
pre_node = result;
a = a->next;
head_state = 0;
continue;
}
//如果不是头结点
polylist temp = (polylist)malloc(sizeof(polynomial_Node));
temp->coef = coef;
temp->expn = expn;
temp->next = nullptr;
pre_node->next = temp;
pre_node = temp;
a = a->next;
}
differentialpoly(result,N-1,result_return);//进入下一阶微分
free(result);//释放内存
}
else if(N==0)//出口,将最终结果复制给result_return
Copy_polylist(a,result_return);
}
//多项式不定积分
void indefiniteintegralpoly(polylist a, polylist &result){
/***********************
Name: indefiniteintegralpoly()
Description: 求多项式不定积分并将结果存储在result的链表中
Input Parameters: -a,需要求不定积分的多项式的第一个结点指针
-result,输入的空结点
Output Parameters: -result,作为函数出口,以result为第一个结点的链表保存了求不定积分后的的多项式
Return: -
Supplement: -
***********************/
result = (polylist)malloc(sizeof(polynomial_Node));
result->coef=0.000;result ->expn=0;result->next=nullptr;
polylist pre_node = result;
while(a!=nullptr){
polylist temp = (polylist)malloc(sizeof(polynomial_Node));
temp->coef = float(a->coef / (float(a->expn) + 1.00));
temp->expn = a->expn + 1;
temp->next = nullptr;
pre_node->next = temp;
pre_node = temp;
a = a->next;
}
}
#endif // NOAH_EXP1_H_INCLUDED
Main.cpp
#include
#include "noah_exp1.h"
#include
#include
using namespace std;
void Menue_gui();
void createandprintpoly();
void addandprint();
void differentialandprint();
void integralandprint();
int main()
{
while(1){
Menue_gui();
int func;
scanf("%d",&func);
switch(func){
case 0:
exit(0);
case 1:
createandprintpoly();break;
case 2:
addandprint();break;
case 3:
differentialandprint();break;
case 4:
integralandprint();break;
default:
printf("Input error! Please try again!");
}
printf("\n");
system("pause");
}
return 0;
}
//菜单界面
void Menue_gui(){
system("cls");//清屏
printf("********************This is Sparse unary polynomial arithmetic unit**************************\n");
printf("*********************************************************************************************\n");
printf("Menue:\n");
printf("\nExit this program------------------------------------------------------0.\n");
printf("\nCreate a polynomial and print it to screen-----------------------------1.\n");
printf("\nAdd 2 polynomial and print result to screen----------------------------2.\n");
printf("\nGet differential of a polynomial and print result to screen------------3.\n");
printf("\nGet indefinite integral of a polynomial and print result to screen-----4.\n");
printf("\n**********************************************************************************************\n");
printf("Choose the function you want to use(input number):\n");
}
//功能1界面
void createandprintpoly(){
system("cls");//清屏
printf("ENTER FUNCTION : Create a polynomial and print it to screen--1.\n");
polylist poly_1;
printf("Please input highest exponential(integer) and a number series of coefficient to initialize the polynomial.\n");
printf("highest exponential:\n");
int Initsize;
scanf("%d",&Initsize);
Initsize=Initsize+1;
//printf("The number series of coefficient:(input)\n");
Creatpolyn(poly_1,Initsize);
printf("Now the polynomial is:\n");
//Displaypolynomial(poly_1);//这是从低次幂到高次幂进行打印
//将正向链表逆置,得到从高次降到低次的链表
polylist poly_1_reverse;
Copy_polylist(poly_1,poly_1_reverse);//复制一个原链表到别的内存空间
poly_1_reverse = revers_Llist(poly_1_reverse);//逆置
Displaypolynomial(poly_1_reverse);
}
//功能2界面
void addandprint(){
system("cls");//清屏
printf("ENTER FUNCTION : Add 2 polynomial and print result to screen----------------------------2.\n");
//初始化多项式A
printf("Initialize polynomial A.\n");
polylist poly_2;
printf("Please input highest exponential(integer) and a number series of coefficient to initialize the polynomial.\n");
printf("highest exponential:\n");
int Initsize;
scanf("%d",&Initsize);
Initsize=Initsize+1;
//printf("The number series of coefficient:(input)\n");
Creatpolyn(poly_2,Initsize);
//初始化多项式B
printf("Initialize polynomial B.\n");
polylist poly_3;
printf("Please input highest exponential(integer) and a number series of coefficient to initialize the polynomial.\n");
printf("highest exponential:\n");
//int Initsize;
scanf("%d",&Initsize);
Initsize=Initsize+1;
//printf("The number series of coefficient:(input)\n");
Creatpolyn(poly_3,Initsize);
//展示多项式A
printf("\nNow the polynomial A is:\n");
polylist poly_2_reverse;
Copy_polylist(poly_2,poly_2_reverse);//复制一个原链表到别的内存空间
poly_2_reverse = revers_Llist(poly_2_reverse);//逆置
Displaypolynomial(poly_2_reverse);
//展示多项式B
printf("\nNow the polynomial B is:\n");
polylist poly_3_reverse;
Copy_polylist(poly_3,poly_3_reverse);//复制一个原链表到别的内存空间
poly_3_reverse = revers_Llist(poly_3_reverse);//逆置
Displaypolynomial(poly_3_reverse);
//多项式A\B相加并打印
printf("\nAdd A and B, the result is:\n");
polylist add_result;
addpoly(poly_2_reverse,poly_3_reverse,add_result);
Displaypolynomial(add_result);
}
//功能3界面
void differentialandprint(){
system("cls");//清屏
printf("ENTER FUNCTION: Get differential of a polynomial and print result to screen------------3.\n");
//初始化多项式C
printf("Initialize polynomial.\n");
polylist poly_5;
printf("Please input highest exponential(integer) and a number series of coefficient to initialize the polynomial.\n");
printf("highest exponential:\n");
int Initsize;
scanf("%d",&Initsize);
Initsize=Initsize+1;
//printf("The number series of coefficient:(input)\n");
Creatpolyn(poly_5,Initsize);
//展示多项式C
printf("\nNow the polynomial is:\n");
polylist poly_5_reverse;
Copy_polylist(poly_5,poly_5_reverse);//复制一个原链表到别的内存空间
poly_5_reverse = revers_Llist(poly_5_reverse);//逆置
Displaypolynomial(poly_5_reverse);
printf("\nInput the differential order:\n");
int N;
scanf("%d",&N);
//一阶微分阶数
printf("\n %d order differential of polynomial is:\n",N);
polylist differential_result_1st;
differentialpoly(poly_5_reverse,N,differential_result_1st);
Displaypolynomial(differential_result_1st);
}
//功能4界面
void integralandprint(){
system("cls");//清屏
//初始化多项式D
printf("Initialize polynomial.\n");
polylist poly_6;
printf("Please input highest exponential(integer) and a number series of coefficient to initialize the polynomial.\n");
printf("highest exponential:\n");
int Initsize;
scanf("%d",&Initsize);
Initsize=Initsize+1;
//printf("The number series of coefficient:(input)\n");
Creatpolyn(poly_6,Initsize);
//展示多项式D
printf("\nNow the polynomial is:\n");
polylist poly_6_reverse;
Copy_polylist(poly_6,poly_6_reverse);//复制一个原链表到别的内存空间
poly_6_reverse = revers_Llist(poly_6_reverse);//逆置
Displaypolynomial(poly_6_reverse);
//不定积分
printf("\n Indefinite integral of polynomial is:\n");
polylist integeral_result;
indefiniteintegralpoly(poly_6_reverse,integeral_result);
Displaypolynomial(integeral_result);
}