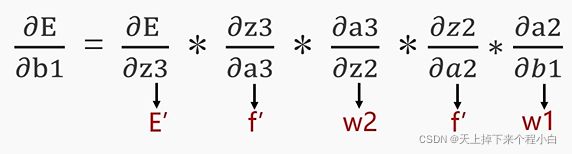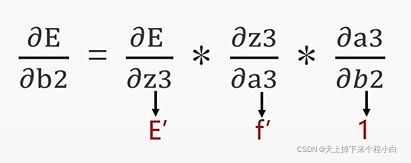BP神经网络
1.BP神经网络是什么
BP(Back-propagation,反向传播)神经网络是最传统的神经网络。也就是使用了Back-propagation算法的神经网络。请注意他不是时下流行的那一套深度学习。要训练深度学习level的网络你是不可以使用这种算法的。原因我们后面解释。而其实机器学习的bottleneck就是成功的突破了非常深的神经网络无法用BP算法来训练的问题。
那么反向传播的东西是什么呢?答案是:误差。就是在模拟过程中(这是一个循环,我们在训练神经网络的时候是要不断的去重复这个过程的)收集系统所产生的误差,并且返回这些误差到输出值,之后用这些误差来调整神经元的权重,这样生成一个可以模拟出原始问题的人工神经网络系统。
2.神经网络基础架构
神经网络其实就是几层神经元,每层神经元里有几个神经元点。不同layer之间的神经元相互连接。其实就是如此:
在这,每一个神经元就是三件事:输入,判断和输出。输入层的神经元(就是那个圆形的圈,代表一个神经元或者一个神经细胞)是读入你输入的数据的。只要你有数据,这个玩意就能跑。这就好比你只要有汽油,汽车就能开是一个道理。中间则是”隐含层。你可以控制这个隐含层的层数,以及每一层里有多少个神经元或者神经细胞。当然在实际操作里为了方便我们一般都直接认为你不管用几层,每层的神经元或者神经细胞数目都是一样的。因为这样的话写代码会比较方便。
3. 运算过程:矩阵乘法
我们要把输入在这个数学结构上传递到输出,要怎么办呢?答案是,使用矩阵乘法。其实这样的思路一开始是非常简单的。 我们以这个例子来说明:
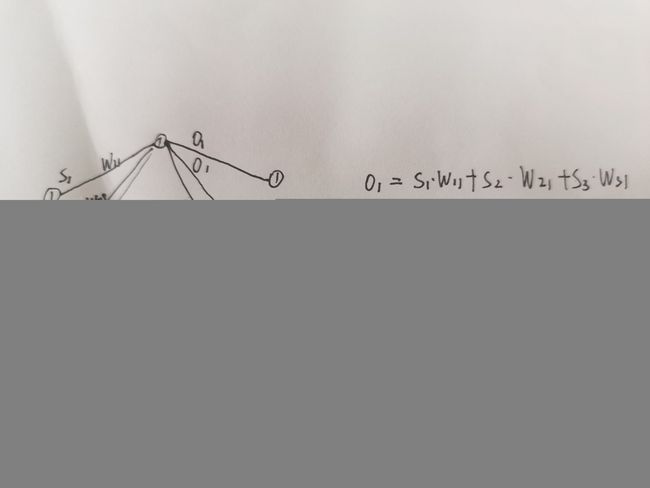
在这幅图里,我们把上一层的第i个神经元和下一层的第j个神经元之间的权重记为w(ij)。而把上一层传入的三个input,分别记为S(1),S(2)和S(3)。
因为数据肯定是在不同的层之间流动的。我们所做的就是通过一个矩阵乘法求解下一层的输出数值。
这个过程其实也非常简单。我们把输出记为O(1),O(2)和O(3)。结合权重,这个其实不就是一个高中生都可以理解的思想吗?以O(1)举例。O(1)里的输出自然有来自S1,2,3的。那么分别按照权重去乘就可以了。权重自然就是一个大于等于零的实数嘛。
O(1)=S(1)*w(11)+S(2)*w(21)+S(3)*w(31)
类似的我们可以求解出O(2)和O(3)。其实答案也很简单:
O(2)=S(1)*w(12)+S(2)*w(22)+S(3)*w(32)
O(3)=S(1)*w(13)+S(2)*w(23)+S(3)*w(33)
写到这里,熟悉矩阵乘法的同学肯定要恍然大悟了。没错,这就是一个矩阵的乘法!最基础的那种。写成矩阵他应该是什么样呢?
其实答案便是:
 我们其实用这种方法,自然可以一层一层的把最左边输入的数据送到最右边来。我们自然可以得到一个结果。但是这个结果有可能是错的吧!所以怎么办呢?我们用真实的结果去和这个结果去比如求差,自然就可以把误差求解出来了。同样的道理,我们可以把误差按照矩阵乘法一路返回。而且在这个过程中,每个神经元和神经线自然可以得到一些”信息“。我们可以用这些信息来修正神经网络,其实也就是给所有的边去赋予不同的权重。
我们其实用这种方法,自然可以一层一层的把最左边输入的数据送到最右边来。我们自然可以得到一个结果。但是这个结果有可能是错的吧!所以怎么办呢?我们用真实的结果去和这个结果去比如求差,自然就可以把误差求解出来了。同样的道理,我们可以把误差按照矩阵乘法一路返回。而且在这个过程中,每个神经元和神经线自然可以得到一些”信息“。我们可以用这些信息来修正神经网络,其实也就是给所有的边去赋予不同的权重。
输出O1,O2,O3与真实值T1,T2,T3自然会有一定的误差,而输入S1,S2,S3是不变的,因此要减小误差损失,就要调节权重矩阵W。
如法炮制。在你有误差E(1),E(2),E(3)的时候,自然可以用这些误差返回上一层,得到上一层应该被返回的误差。其实也是一个矩阵乘法的内容。
4. 如何去调参数:微积分(其实就是梯度下降)
其实这就是我们使用了人工神经网络来模拟学习的过程。理论上,这个算法可以处理世界上的任何问题。无论是股票交易还是生物信息,无论是飞机上天还是潜艇下水。当然了,工程就是另一回事了。
那么这些权重是如何被求解出来的呢?答案便是:微积分。
首先说明,这里我们使用Sigmoid函数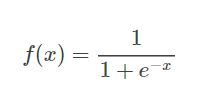 作为激活函数,其作用详见这篇文章。
作为激活函数,其作用详见这篇文章。
![]()
整体框架如下:
在我们的获得预测结果后,我们通过反向传播对w(权重)和b(偏置:相当于y=ax+b中的b)进行梯度调整,从而得到最优的w和b。最后在应用调整后的模型进行测试
1.前向传播
[注]:S(a2)意为对a2进行Sigmoid函数激活,其余同理。
最终得到前向传播结果z3。他与真实值T有一定的误差。
2.误差反向传播
y*即为z3,y为真实值T,两者相减平方除以2求均方误差E,通过梯度下降对其中的参数b1,w1,b2,w2进行调整。(不明白梯度下降的参考此文章)
1.对b1进行求导:
f'为sigmoid的导数 。
2.对b2进行求导:
3.对w1进行求导:
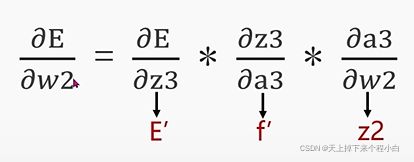
4.对w2进行求导:
以b1为例进行梯度下降求最优解:
同理可对b2,w1,w2进行调整,逐步找到最优解。
当迭代次数超过一定数值,即迭代次数足够大或误差小于某个值时,便停止迭代,此时的权重矩阵w和偏置b即为最优解。
BP神经网络就是通过前向传播得到误差,反向传播调整误差,再前向传播,再反向传播一轮一轮得到最优解的。