回溯法（基础版）

“能进则进,不能进则换,不能换则退,退一步海阔天空。”

---

算法适用问题

搜索问题(求解的个数)/最优解问题

算法思想步骤

深度优先搜索

1. 定义解空间
   解的组织形式：一个n元组{x${}_1$,x${}_2$,x${}_3$,……,x${}_n$}。
   显约束：对解分量x${}_i$取值范围的限定，控制解空间的大小。
2. 确定解空间的组织结构
   通常用解空间树形象表示。一般为子集树、排列数、m叉树等等。
3. 搜索解空间
   根据隐约束即剪枝函数（约束函数->找可行解和限界函数->找最优解）搜索解，若当前结点满足条件，继续向下搜索，若不满足返回上一级结点。

子集树、m叉树：
void backtrack(int t)          //t表示递归深度，即当前扩展节点在解空间树的深度
{ 
    if ( t > n ) output(x);    //n控制递归深度，如果算法已经搜索到叶节点，记录输出可行解X
    else
    {
        for(int i = f(n,t) ; i <= g(n,t) ; i++)  //在深度t，i从未搜索过得起始编号到终止编号
        {
            x[t] = h(i);       //查看i这个点的值是否满足题目的要求
            if( constraint(t) && bound(t)) 
                backtrack(t+1)
       //constraint（t）为true表示在当前扩展节点处x[1:t]的取值满足问题的约束条件；
       //bound(t)为true表示当前扩展节点取值没有使目标函数越界；
       //为true表示还需要进一步的搜索子树，否则减去子树。
         }
    }
}

排列树:
void backtrack(int t)          //t表示递归深度，即当前扩展节点在解空间树的深度
{ 
    if ( t > n ) output(x);    //n控制递归深度，如果算法已经搜索到叶节点，记录输出可行解X
    else
    {
        for(int i = f(n,t) ; i <= g(n,t) ; i++)  //在深度t，i从未搜索过得起始编号到终止编号
        {
            swap(x[t],x[i]);
            if( constraint(t) && bound(t)) 
                backtrack(t+1)
            swap(x[t],x[i]);
       //constraint（t）为true表示在当前扩展节点处x[1:t]的取值满足问题的约束条件；
       //bound(t)为true表示当前扩展节点取值没有使目标函数越界；
       //为true表示还需要进一步的搜索子树，否则减去子树。
         }
    }
}

---

基础题目

---

A.装载问题

有两艘货船,载重分别为w1、w2,物品总重量不超过载重总量w1+w2,问物品是否都可以装下。如,w1=w2=10，物品c1=c2=9,c3=2,则无法装下;c1=c2=5，c3=10,则可以装下。
基本思路：问题可以等价于，使第一艘货船尽可能装满，看剩下的物品能否装入第二艘货船

1. 定义解空间
   开始装第一艘货船， 对于每个物品只有拿与不拿两种选择。所以解空间为{x${}_1$,x${}_2$,x${}_3$,……,x${}_n$}。显约束x${}_i$=0或1，i=1,2,3…,n。有2${}^n$种解。
2. 确定解空间树
   子集树。
3. 搜索解空间
   约束条件：判断装入第一艘货船的物品总重量是否超出第一艘货船的容量。 （${\sum }_{i=1}^n{c}_i{x}_i$$<=W_1$）
   限界条件：如果要选择第t个分量,目前的重量加上剩余的所有重量，都没有当前最优解的重量大，放弃向下搜索，剪枝。
   $cw={\sum }_{i=1}^{t-1}{c}_i{x}_i$(当前载重量)
   $r={\sum }_{i=t}^n{c}_i{x}_i$(剩余物品总重量)
   bestw=当前最优解
   $(cw+r>bestw)$

#include
#define M 105
using namespace std;

int n; //物品个数 
double W1,W2; //两艘货船载重 
double cw; //当前重量 
double bestw;  //将第一艘货船尽可能装满 
double c[M],x[M]; //每个物品的重量 

double Bound(int i) //计算上界cw+r
{
	double r=0;
	while(i<=n)
	{
		r=r+c[i];
		i++;
	}
	return cw+r; 
} 
 
void Backtrack(int t)
{
	if(t>n) //找到一个最优解 
	{
		bestw=cw;
		return ;
	}
	if(cw+c[t]<=W1) //满足约束条件,搜索放入该物品的子树 
	{
		x[t]=1;
		cw=cw+c[t];
		Backtrack(t+1);
		cw=cw-c[t];
	}
	if(Bound(t+1)>bestw) 
	{
		x[t]=0;
		Backtrack(t+1);
	}
 } 
 
 void Init(double W,int n) //初始化 
 {
 	cw=0;
 	bestw=0;
 	double sumw=0;
 	for(int i=1;i<=n;i++)
 	sumw=sumw+c[i];
 	if(sumw<=W)
 	{
	 cout<<"Yes"<<endl;
	 return ;		
	}
	Backtrack(1); 
	if(sumw-bestw<=W2)
	{
		cout<<"Yes"<<endl;
		return ;
	}
	else
	{
	    cout<<"No"<<endl;
		return ;	
	}
}

int main()
{
	cout<<"物品总数为:";
	cin>>n;
	cout<<"两艘货船的载重为:";
	cin>>W1>>W2;
	cout<<"依次输入每个物品的重量"<<endl; 
	for(int i=1;i<=n;i++)
	cin>>c[i];
	Init(W1,n);
	return 0;	 
}

B.0-1背包问题

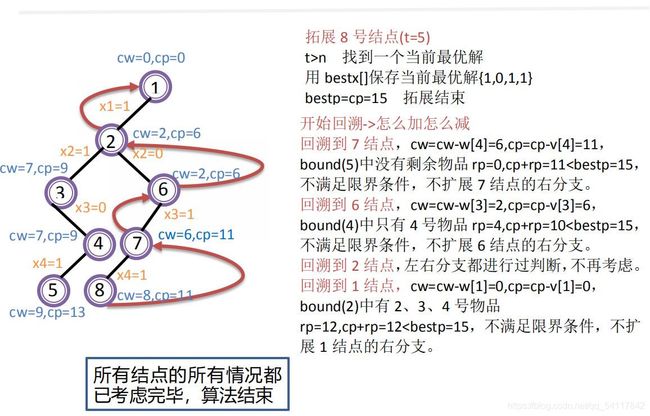
给定n种物品和一背包。物品 i 的重量为 wi，其价值为 vi，背包的容量为 W。问应该如何选择装入背包中的物品，使得装入背包中物品的总价值最大？

1. 定义解空间
   对于每个物品只有拿与不拿两种选择。所以解空间为{x${}_1$,x${}_2$,x${}_3$,……,x${}_n$}。显约束x${}_i$=0或1，i=1,2,3…,n。有2${}^n$种解。
2. 确定解空间树
   子集树。在搜索的时候，左节点是可行节点的时候，搜索就进入左子树。当右子树可能包含最优解的时候，就进入右子树搜索。否则减去右子树。
3. 搜索解空间
   约束条件：判断装入购物车的物品总重量是否超出购物车的容量。
   （${\sum }_{i=1}^n{w}_i{x}_i$<=W）
   限界条件：对于任意一个中间结点z，从根节点到z的分支状态已经确定，从z到子孙结点的分支状态是不确定的。即若z所在解空间树的层数是t，则第一种物品到第t-1种物品的状态已经确定，第t-1种物品到第n种物品的状态还没有确定。前t种物品的状态确定后，当前已装入购物车的总价值用cp表示。第t+1种物品到第n种物品的具体状态未定，假设全部装入购物车，第t+1种物品到第n种物品的总价值用rp表示。所以cp+rp是从跟出发经过中间节点z的可行解的价值上界。如果价值上界小于或等于当前搜索的最优值(bestp,初值为0)，则说明从z向下继续搜索不可能得到一个更优的解，即没有搜索下去的必要，反之继续从z向下搜索。即限界条件为 cp+rp>bestp。

图解

#include
#define M 105
using namespace std;

int n;  //物品总数 
double W; //购物车容量 
int x[M];  //当前每个物品的状态 
double w[M],v[M]; // 物品的重量与价值 
double cw;  //购物车当前重量 
double cp;  //购物车当前价值 
double bestp;  //当前最优价值 
int bestx[M];  //当前最优解 

double Bound(int i) //计算上界（已装物品价值+剩余物品i~n总价值） 
{
	double rp=0;
	while(i<=n) //依次计算剩余物品价值 
	{
		rp=rp+v[i];
		i++;
	}
	return cp+rp; //返回上界 
}

void Backtrack(int t)  // 当前判断结点在第t层 
{
	if(t>n) //已到达叶子结点 
	{
		for(int j=1;j<=n;j++)
		{
			bestx[j]=x[j];
		}
		bestp=cp; //保存当前最优解 
		return ;
	}
	 if(cw+w[t]<=W) //当前结点满足约束条件继续向左分支搜索 
	 {
	 	x[t]=1;
		cw=cw+w[t];
		cp=cp+v[t];
		Backtrack(t+1);
		cw=cw-w[t];
		cp=cp-v[t]; 
	 }	 
	 if(Bound(t+1)>bestp) //当前结点满足限界条件继续向右分支搜索 
	 {
	 	x[t]=0;
		Backtrack(t+1); 
	 } 
}

void Knapsack(double W,int n)
{
	//初始化
	cw=0;cp=0;bestp=0;
	double sumw=0.0,sumv=0.0; //统计物品总价值与总重量 
	for (int i=1;i<=n;i++)
	{
		sumv=sumv+v[i];
		sumw=sumw+w[i];
	}
	if(sumw<=W)
	{
		bestp=sumv;
		cout<<"放入购物车最大价值为"<<bestp<<endl;
		cout<<"所有物品均放入购物车"; 
		return;
	} 
	Backtrack(1);
	cout<<"放入购物车最大价值为"<<bestp<<endl;
	cout<<"放入购物车的物品序号为"<<endl;
	for(int i=1;i<=n;i++)
		if(bestx[i]) cout<<i<<" ";
}

int main()
{
	cout<<"请输入物品个数";
	cin>>n;
	cout<<"请输入购物车容量";
	cin>>W;
	cout<<"请依次输入每个物品的重量与价值";
	for(int i=1;i<=n;i++)
	{
		cin>>w[i]>>v[i];
	}
	Knapsack(W,n);
	return 0;
 } 

C.N皇后问题

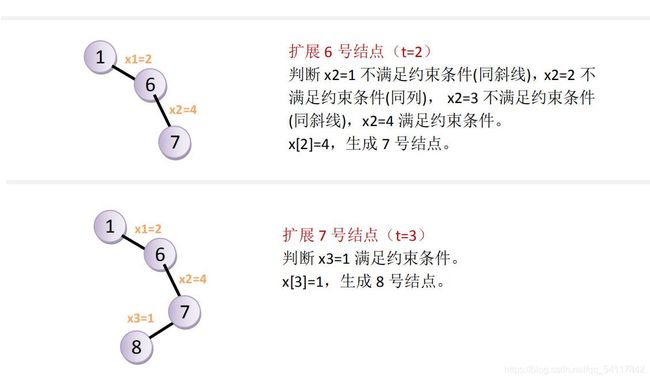
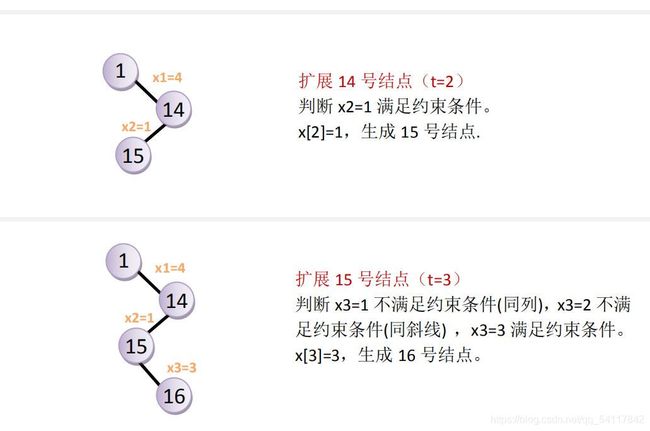
设计一种算法，打印 N 皇后在 N × N 棋盘上的各种摆法，其中每个皇后都不同行、不同列，也不在对角线上。这里的“对角线”指的是所有的对角线，不只是平分整个棋盘的那两条对角线。

1. 定义解空间
   以行为主导
   n元组{x${}_1$,x${}_2$,x${}_3$,……,x${}_n$}。x${}_i$表示第i个皇后在第i行第x${}_i$列，显约束x${}_i$=1，2，…,n。
2. 确定解空间树
   m(m=n)叉树，深度为n。
3. 搜索解空间
   约束条件：在第i行放置第i个皇后时，这个皇后不能与j行皇后同列、同斜线。 即**x${}_i$!=x${}_j$且$|i-j|$!=|x${}_i$- x${}_j$| ** 。
   限界条件：本题不求最优解只求可行解所以无限界条件。

图解

#include 
#define M 105 
using namespace std;
 
int n; //n皇后
int x[M]; //存放每个皇后存放列数
int countn=0; //可行解的个数 
 
bool Place(int t)//约束函数，判断第t个皇后能否放在第i个位置
{
	bool ok=true;
	for(int j=1;j<t;j++)
	{
		if(x[t]==x[j]||t-j==fabs(x[t]-x[j]))
		{
			ok=false;
			break;
		}
	}
	return ok;
}

void Backtrack(int t)//搜索求解 
{
	if(t>n) //找到一个可行解 
	{
		countn++;
		for(int i=1;i<=n;i++ ) //打印位置 
		cout<<x[i]<<" ";
		cout<<endl;
	}
	else
	{
		for(int i=1;i<=n;i++) //分别判断第t层的n个分支 
		{
			x[t]=i;
			if(Place(t))
			Backtrack(t+1); 
		 }		 
	}
}

int main()
{
	cin>>n;
	Backtrack(1);
	cout<<"有"<<countn<<"个可行解"; 
}  

D.涂色问题

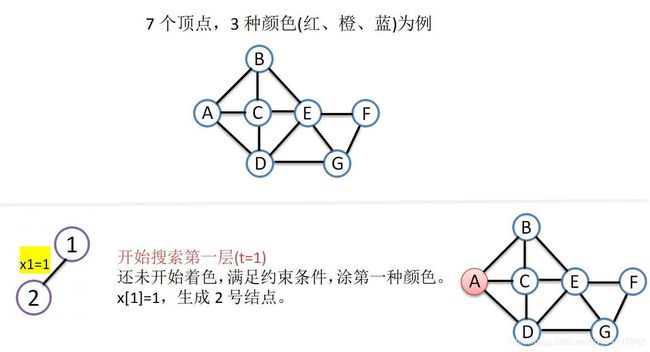
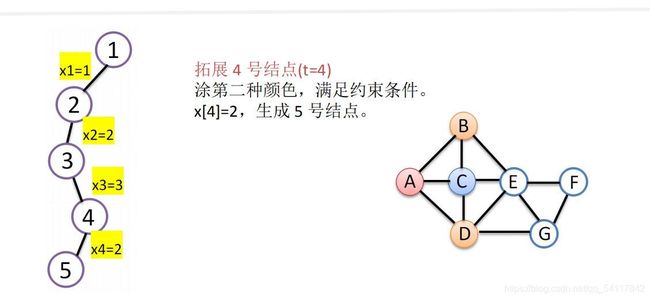
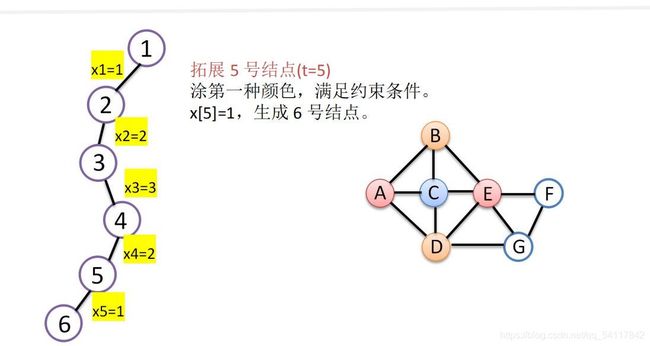
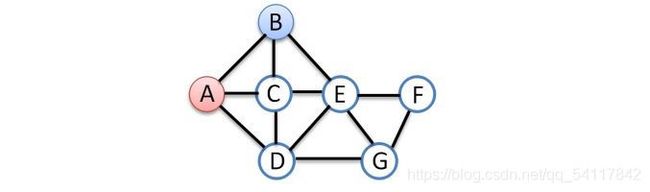
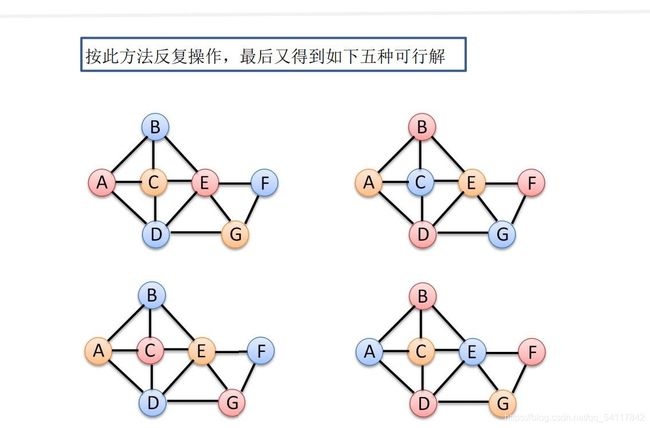
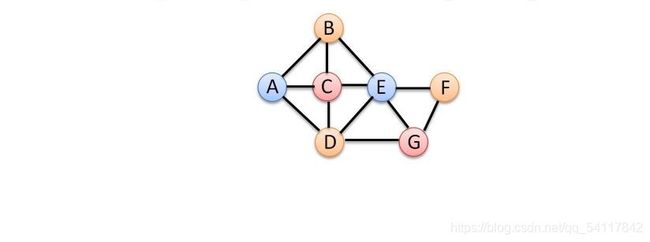
给定无向连通图G=(V, E)和m种不同的颜色，用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中相邻的两个顶点有不同的颜色。找出所有着色方案。

1. 定义解空间
   n元组{x${}_1$，x${}_2$，x${}_3$，……，x${}_n$}。x${}_i$表示第i个顶点是第几种颜色，显约束x${}_i$=1，2，…，m。
2. 确定解空间树
   m叉树，深度为n。
3. 搜索解空间
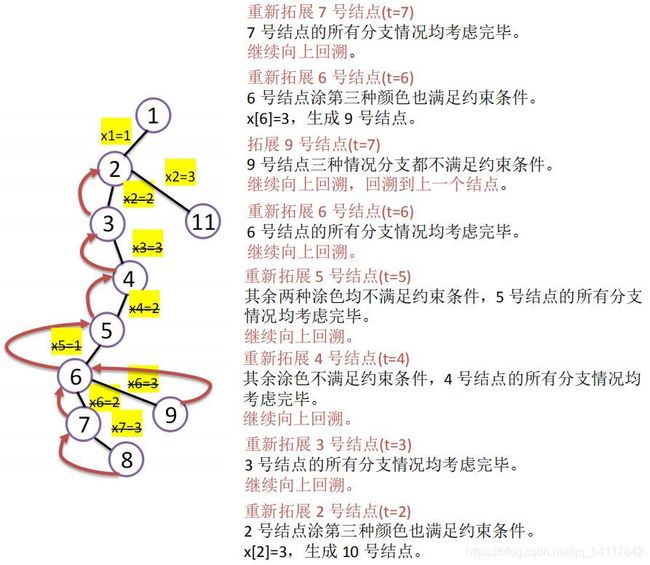
   约束条件：假设当前扩展结点处于解空间树第t层，则第1到t-1个结点的色号已经确定，继续拓展则需判断第t个结点的色号是否与前t-1个结点中与其有边相连的结点颜色相同。若不相同用此色号；若相同，换下一个色号尝试。
   限界条件：只需寻找可行解，无需限界条件。

图解

#include
#define M 105
using namespace std;

int sum;  //可行解的个数
int x[M];  //记录每一次可行解
int n,m,edge;  //顶点数、颜色数、边数
int Map[M][M]; //邻接矩阵表示图 

bool OK(int t) //约束条件
{
	for(int j=1;j<t;j++)
	{
		if(Map[t][j])  //t与j有边相连
		{
			if(x[j]==x[t])  //判断t与j色号是否相同
			return false; 
		} 
	}
	return true;
}

void Backtrack(int t)  //搜索函数
{
	if(t>n)  //找到一个可行解 
	{
		sum++;
		cout<<"第"<<sum<<"种方案为:" ;
		for(int i=1;i<=n;i++)
		 cout<<x[i]<<" ";
		cout<<endl;
	}
	else
	{
		for(int i=1;i<=m;i++) //每个结点尝试m种颜色 
		{
			x[t]=i;
			if(OK(t))
			 Backtrack(t+1);
		}
	}
}

void CreatMap()
{
	int u,v;
	cout<<"请输入无向图的边数:";
	cin>>edge;
	memset(Map,0,sizeof(Map)); //邻接矩阵里面数据初始化为0 
	cout<<"请依次输入有边相连的两个结点"<<endl;
	for(int i=0;i<edge;i++)
	{
		cin>>u>>v;
		Map[u][v]=Map[v][u]=1; 
	} 
	Backtrack(1);
}

int main() 
{
	cout<<"请输入顶点数:";
	cin>>n;
	cout<<"请输入颜色数:";
	cin>>m;
	CreatMap();
}