PU-Learning 原理介绍
解决问题
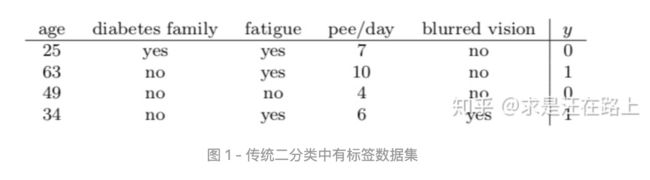
在实际分类场景中,经常会遇到类似这样的问题:只有已标记的正样本,以及未标记的样本。比如金融风控场景,只有部分用户被标记为欺诈用户,剩下的大量用户未被标记。虽然这其中大多数信用良好,但仍有少量可能为欺诈用户。
为了方便操作,我们可以将未标记的样本都作为负样本进行训练,但存在几个缺陷:
- 正负样本极度不平衡,负样本数量远远超过正样本,效果很差。
- 某些关键样本会干扰分类器的最优分隔面的选择,尤其是SVM。
如何辨别未标记样本中的正负样本,提升模型准确度,就成为一个值得思考的问题。PU Learning就是解决这种场景的一种学习方法。
基本概念
PU-Learning的目标与传统二分类问题一致,都是为了训练一个分类器用以区分正负样本。不同点在于:此时只有少数已标注的正样本,并没有负样本。
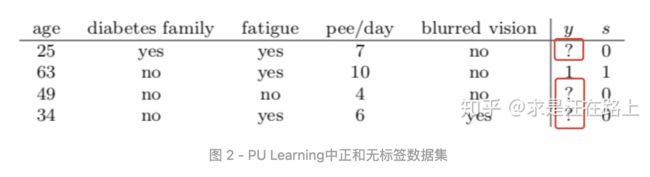
图2是一个典型的PU数据示例。s表示是否被标注。在PU问题中,如果某个样本被标注,则属于P集合,否则该样本标签未知,属于U集合。
事实上,这是因为:即使是领域专家,在很多案例中也难以保证判断的准确率。根据反证法的思想,专家对于判定为黑(正)的往往比较有信心,因为通常有证据可循,只要命中硬规则即可。然而要判定为白(负),则需要排除所有不可能,这在事实上是难以真正做到的,因为我们收集到的信息总是有限的。
为了维护一个充分可靠的P集合,我们要求专家在进行标注时,仅把具有充分信心的样本标注为1,保证P集合的正确性。而对于专家标注的0无法完全信任,因此会选择将标为0的样本重新放入U集合中,假装没有标注过。整个标注过程如图3所示。
根据PU问题的一般设定,只要一个样例被标注,那么其就是正样本。
Q:如何从U集合中拿样本?
可以采取某种打标机制(Labeling Mechanism)从U中选择样本。同时,最理想的情况是每次都是从U集合中的隐式的“P”集合中选择,再经专家标注验证后,加入显式的P集合中。这样可以节省很多成本,P集合也能得到快速扩充!
在信贷风控中,通常利用信用评分卡给客户打分,按信用分排序后,就可以进行拒绝或放贷。同样地,需要定义一个倾向评分模型(Propensity Score),用以预测U集合中样本被选中的可能性(倾向)。
基本假设
PU-Learning的问题设定:
- 一个是P集合,一个是U集合;
- 有标注即为正样本,即有标注和正样本是等价的;
Q:为什么有样本没有标注?
- 是负样本,按PU Learning的定义,对于专家标注的0无法完全信任,因此会选择将标为0的样本重新放入U集合中,假装没有标注过。
- 是正样本。只是没有被打标机制所选中,所以无法观察到其表现。
打标机制(Label Mechanism)
介绍构建选择模型时的一些假设
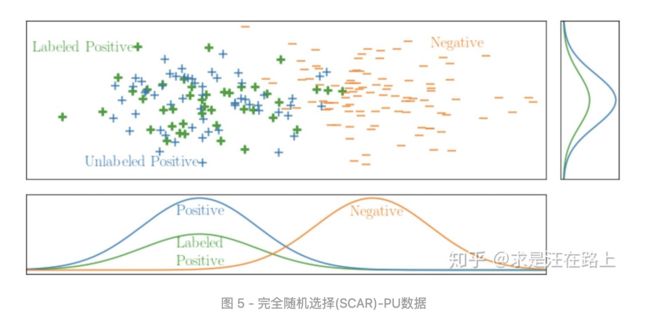
假设1:完全随机选择(Selected Completely At Random,SCAR)
有标签样本完全是从正样本分布中随机选择的,且与本身的特征属性无关。
如图5所示,从x和y两个维度观察,x轴和y轴都是无偏均匀采样。此时,倾向评分函数是常数,也就是说在所有样本上一视同仁,失去了排序性。
假设2:随机选择(Selected At Random,SAR)
有标签样本是从正样本分布中随机选择的,但与本身的特征属性有关。
如图6和图7所示,从x和y两个维度观察,虽然y轴上是均匀采样,但x轴上并不是,说明是有偏采样。造成这个现象的主要原因是——根据样本属性进行筛选。
假设3:概率差距(Probabilistic Gap,PG)
正负预测概率差距越大,被选中打标的概率也就越大。
数据假设(Data Assumptions)
对样本属性、标签等方面提出假设
假设4:负向性(Negativity)
假设U集合所有样本都属于负类。
尽管该假设不符合常理,但在实践中经常采用。主要原因在于:
- 已有P集合,只需要再有N集合,就可以直接归于成熟的二分类问题来解决。
- 作为EM算法中初始化的第一步,把U集合等同于N集合,然后不断迭代修正,最终收敛到一个稳态。
假设5:可分性(Separability)
始终存在一个分类器,能把正负两类然完全分开。
该假设主要是为了保证正负样本可分。在假设空间中,存在一个分界阈值,高于阈值预测为正样本,反之为负样本。
假设6:平滑性(Smoothness)
如果两个样本相似,那么预测概率评分也是基本一致的,不会存在跃变的情况。
该假设能保证可靠负样本是那些远离P集合中的所有样本。为此,很多人针对相似度(也就是距离)的衡量开展了各种研究。
PU-Learning的评估指标
- 准确率:表示预测为1的样本中,实际标签为1的样本的占比。
- 召回率:表示实际标签为1的样本里,预测为1的样本的占比。
两阶段技术(Two-step PU Learning)
基于可分性和平滑性假设,所有正样本都与有标签样本相似,而与负样本不同。
整体流程一般可分解为以下3个步骤:
- step 1: 从U集合中识别出可靠负样本(Reliable Negative,RN)。
- step 2: 利用P集合和RN集合组成训练集,训练一个传统的二分类模型
- step 3: 根据某种策略,从迭代生成的多个模型中选择最优的模型。
Q:可靠负样本的定义是什么?
基于平滑性假设,样本属性相似时,其标签也基本相同。换言之,可靠负样本就是那些与正样本相似度很低的样本。那么,问题的关键就是定义相似度,或者说距离(distance)。
识别可靠负样本
1)间谍技术(The Spy Technique)
- step 1:从P中随机选择一些正样本S,放入U中作为间谍样本(spy)。此时样本集变为P-S和U+S。其中,从P中划分子集S的数量比例一般为15%。
- step 2:使用P-S作为正样本,U+S作为负样本,利用迭代的EM算法进行分类。初始化时,把所有无标签样本当作负类,训练一个分类器,对所有样本预测概率 。
- step 3:以spy样本分布的最小值作为阈值,U中所有低于这个阈值的样本认为是RN。
注意:spy样本需要有足够量,否则结果可信度低。
2)1-DNF技术
- step 1:获取PU数据中的所有特征,构成特征集合F。
- step 2:对于每个特征,如果其在P集合中的出现频次大于N集合,记该特征为正特征(Positive Feature,PF),所有满足该条件的特征组成一个PF集合。
- step 3:对U中的每个样本,如果其不包含PF集合中的任意一个特征,则将该样本加入RN。
训练分类器
在识别出可靠负样本后,进行分类器的训练:
# 样本准备:P 和 RN 组成训练集X_train; P给定标签1,RN给定标签0,组成训练集标签y_train # 用 X_train 和 y_train 训练逻辑回归模型 model model.fit(X_train, y_train) # 用 model 对 Q 进行预测(分类)得到结果 prob Q = U - RN # 无标签样本集U中剔除RN prob = model.predict(Q) # 找出 Q 中被判定为负的数据组成集合 W predict_label = np.where(prob < 0.5, 0, 1).T[0] negative_index = np.where(predict_label == 0) W = Q[negative_index] # 将 W 和 RN 合并作为新的 RN,同时将 W 从 Q 中排除 RN = np.concatenate((RN, W)) # RN = RN + W Q = np.delete(Q, negative_index, axis=0) # Q = Q - W # 用新的 RN 和 P 组成新的 X_train,对应生成新的 y_train # 继续训练模型,扩充 RN,直至 W 为空集,循环结束。 # 其中每次循环都会得到一个分类器 model ,加入模型集 model_list 中
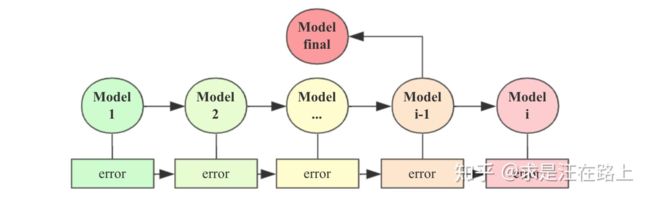
最优模型选择
从每次循环生成的分类器中,制定选择策略,选出一个最佳分类器。
1)预测误差提升差
训练的目标肯定是让模型的预测误差最小,因此,当预测误差提升差小于0时,说明当前一轮i比i-1轮模型的误差开始升高。我们就选择i-1轮训练的模型。
图 10 - 模型迭代和选择过程
2)F1值提升比
当F1值提升比>1时 ,说明模型性能在提升。因此,选择最后一次提升的模型。
3)投票(Vote)
对每轮迭代生成的模型model,进行加权组合成最终模型。
4)最后(Last)
直接选用最后一次迭代生成的分类器。
5) 假阴率(FNR > 5 %)
当超过已标注正样本的5%被错误预测为负类时,迭代停止。
用Python伪代码组织上述流程:
# 直接选用最后一次循环得到的分类器:
final_model = model_list[-1]
# 利用规则选出一个最佳分类器:
# 用最后一次循环得到的分类器 S-last 对 P 进行分类。
# 若分类结果中有超过8%条数据被判定为负,则选用第一次循环的分类器S-1。
# 否则继续选用 S-last 作为最终分类器
neg_predict = model_list[-1].predict(P)
neg_predict = np.where(neg_predict < 0.5, 0, 1).T[0]
if list(neg_predict).count(0) / neg_predict.shape[0] > 0.08:
final_model = model_list[0]
else:
final_model = model_list[-1]
# 对测试数据集进行分类
result = final_model.predict(X_test)
有偏学习(Biased PU Learning)
有偏PU Learning的思想是,把无标签样本当作带有噪声的负样本。那么,该如何把噪声考虑进PU问题模型学习过程?可以采取以下方式:
- 噪声引起误分类,因此对错误分类的正样本置于更高的惩罚。
- 基于适合PU问题的评估指标来调整模型参数。
Active Learning与PU Learning的对比
两者都是为了解决:针对有标签样本很少的情况,如何去训练一个二分类模型?
在Active Learning中,专家会多次标注,逐渐扩充L(Labeled)集合,active learner则会在多次学习L集合(包含正负样本)时不停提升自己的性能,我们称之为LU setting。在打标过程中,其有以下特点:
- 选择策略:在从U集合中选择样本时,选择策略与模型密切相关。例如,不确定性策略是选择模型最不确定的样本进行标注。
- L集合产物:在模型迭代过程中,积累的L集合包括P(Positive)和N(Negative),但其没有考虑到负样本的标注实际并不可靠这一问题。
- 人机交互:对人的依赖严重,需要人和模型之间交互频繁。
在PU Learning中,同样需要借助人工打标,Learner则在每次迭代的时候,基于PU数据进行学习,我们称之为PU setting。但差异点在于:
- 选择策略:在从U集合中选择样本时,选择策略与模型相关性低,主要依赖于样本自身之间的差异。例如,1-DNF技术致力于寻找正负样本显著差异的强特征集合。
- L集合产物:积累的L集合只包括P(Positive)。在Two-step PU Learning中,可靠负样本RN只是在模型迭代过程中的一个虚拟产物,我们总是认为负样本的标签是不可靠的。
- 人机交互:依赖相对较少。作为半监督学习的一种,在初始化后,可以依赖EM算法自动迭代。
参考文献
- 《PU Learning在风控中的应用(理论篇)》:PU Learning在风控中的应用(理论篇) - 知乎;