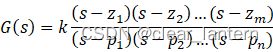MATLAB实现控制系统模型(传递函数)的建立与转化,传递函数模型与零极点增益模型的转化,连续系统与离散系统的转化,对比不同采样周期对系统性能的影响
最近使用MATLAB做了很多控制工程方面的仿真,测试不同系统的响应和特性。不得不说使用MATLAB做控制仿真还是十分简洁方便的,尤其是其中的simulink模块可以提供更加直观的模型,方便分析与测试。今天就分享在matlab中构造传递函数模型,并可将其转化为零极点模型,以及实现连续系统与离散系统的转化。并设计一个简单的系统,对比不同采样周期对系统性能的影响。
首先我们都知道一般传递函数的形式:
零极点模型即是根据传递函数的分子和分母上的多项式的根看作该分式的零点和极点。事实上,分别给定一个传递函数的零点和极点的值以及个数,在特定倍数k下,该传递函数就被确定了。零极点模型的传递函数的形式如下:
事实上,零极点模型的传递函数在实际应用中是更方便的,尤其在不确定系统的传递函数情况下,对系统进行系统辨识的过程中,可以测试不同的零点和极点的个数,观察系统的响应特性。而且MATLAB中自带的函数,在脚本中即可以将传递函数在这两种模型中转变。
首先将一个常规的传递模型转为零极点增益模型。代码如下:
num=[1,-1.3,0.3];
den=[1,3,2.5,0.5];
T=1;
Gs1=tf(num,den)
[z,p,k]=tf2zp(num,den);
Gz1=zpk(z,p,k,T)设置的采样时间为1秒,运行结果为:
Gs1 =
s^2 - 1.3 s + 0.3
-------------------------
s^3 + 3 s^2 + 2.5 s + 0.5
Continuous-time transfer function.
Gz1 =
(z-1) (z-0.3)
--------------------------
(z+1.707) (z+1) (z+0.2929)
Sample time: 1 seconds
Discrete-time zero/pole/gain model.
可见已将一个连续的传递函数模型以采样周期为1的零极点增益模型。
同样的,也可直接设置一个零极点增益模型,将其转化为连续系统的传递函数。
代码如下:
z=[0.3,0.5];
p=[-1,-0.3,-0.2];
k=[3];
T=1;
Gz2=zpk(z,p,k,T)
[num,den]=zp2tf(z',p',k);
Gs2=tf(num,den)运行结果:
Gz2 =
3 (z-0.3) (z-0.5)
---------------------
(z+1) (z+0.3) (z+0.2)
Sample time: 1 seconds
Discrete-time zero/pole/gain model.
Gs2 =
3 s^2 - 2.4 s + 0.45
-----------------------------
s^3 + 1.5 s^2 + 0.56 s + 0.06
Continuous-time transfer function.
此外,将连续系统离散化也是在各个工程领域的基本操作。在实际中,纯粹数学意义上的连续、导数、微分等概念都是不可能实现的,只能在一定精度范围内使用离散化手段,将连续模型离散化。离散的精度往往取决于采样周期或分辨率,也决定着控制系统的精度。
MATLAB中自带很多方法可以实现,连续系统模型与离散系统模型的相互转化:
| 连续模型-->离散模型 | 离散模型-->连续模型 |
|---|---|
| Gz = c2d(Gs,T,'使用方法') | Gs = d2c(Gz,T,'使用方法') |
| zoh:零阶保持器法 | zoh:零阶保持器法 |
| foh:一阶保持器法 | foh:一阶保持器法 |
| imp:脉冲响应不变法 | imp:脉冲响应不变法 |
| tustin:双线性变换法 | tustin:双线性变换法 |
| matched:零极点匹配法 | matched:零极点匹配法 |
现在设计一个简单的一阶系统,为两个传递函数串联,并将输出反馈回输入,对比不同采样周期下的系统响应曲线。
代码如下:
num=[10,1];
den=[1,1];
T=[0.1,0.5,1];
Gs1=tf(num,den);
Gz1=c2d(Gs1,T(1),'zoh');
Gz2=c2d(Gs1,T(2),'zoh');
Gz3=c2d(Gs1,T(3),'zoh');
Gs4=tf([1],[10,1,0]);
Gz4=c2d(Gs4,T(1),'zoh');
Gz5=c2d(Gs4,T(2),'zoh');
Gz6=c2d(Gs4,T(3),'zoh');
GS1 = Gs1*Gs4;
GZ1 = Gz1*Gz4;
GZ2 = Gz2*Gz5;
GZ3 = Gz3*Gz6;
G1=feedback(GS1,1);
G2=feedback(GZ1,1);
G3=feedback(GZ2,1);
G4=feedback(GZ3,1);
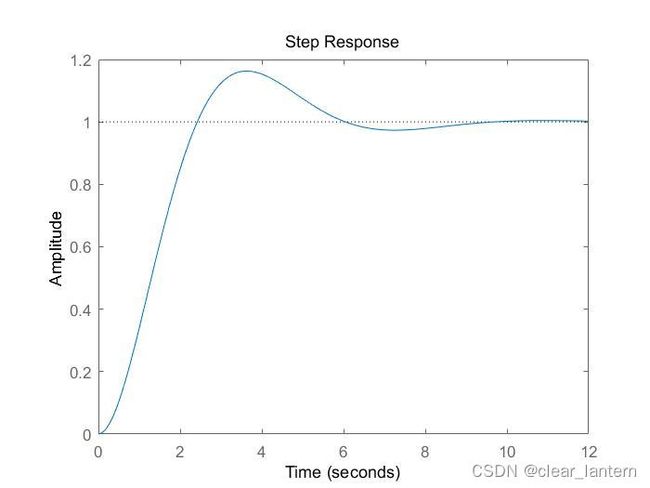
step(G1);
hold on;
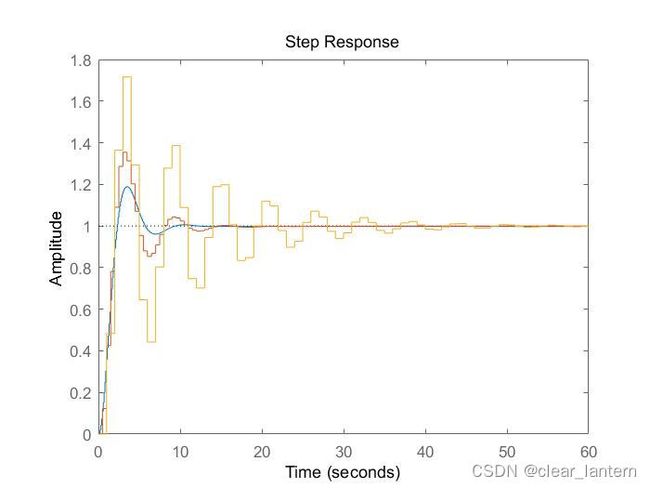
figure()
step(G2,G3,G4);传递函数串联可直接在脚本中相乘,分别设置采样周期为0.1、0.5、1。运行结果为:
可见,采样周期越大,系统的离散程度越大,精度就越低,超调量和调整时间都变大。
本文章适合学习控制工程的初学者浏览,代码大部分是直观好理解的。feedback(Gs1,Gs2)表示将Gs2的输出反馈给Gs1。观察某一传递函数的阶跃响应可以直接step(Gs)。