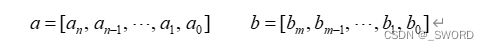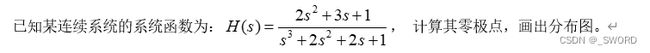【MATLAB】自控建模第一节--传输函数与零极点图

1. 连续系统的时域响应

        连续时间LTI系统可用如下的线性常系数微分方程来描述：

        已知输入信号x(t)以及系统初始状态，就可以求出系统的响应。MATLAB提供了微分方程的数值计算的函数，可以计算上述n阶微分方程描述的连续系统的响应，包括系统的单位冲激响应、单位阶跃响应、零输入响应、零状态响应和完全响应。

        在调用MATLAB函数时，需要利用连续系统对应的系数函数。对微分方程进行Laplace变换即可得系统函数：

在MATLAB中可使用向量和向量分别保存分母多项式和分子多项式的系数：

   

这些系数均按s的降幂直至s0排列。

(1) 连续系统的单位冲激响应h(t)的计算

impulse(sys)计算并画出系统的冲激响应。参数：sys可由函数tf(b,a)获得。其中： 

h=impulse(sys, t): 计算并画出系统在向量t定义的区间上的冲激响应，向量h保存对应区间的系统冲激响应的输出值。

(2) 连续系统的单位阶跃响应h(t)的计算

step(sys): 计算并画出系统的阶跃响应。

g=step(sys, t): 计算并画出系统在向量t定义的区间上的阶跃响应，向量g保存对应区间的系统阶跃响应的输出值。

(3) 连续系统的零状态响应y(t)的计算

lsim(sys, x, t) 计算并画出系统的零状态响应。参数 sys可由函数tf(b,a)获得,  x为输入信号，t为定义的时间向量。

2．连续系统的系统函数零极点分析

        系统函数H(s)的极点pi决定了冲激响应h(t)的基本形式，而零点和极点共同确定了冲激响应h(t)的幅值。

        MATLAB中提供了roots函数计算系统的零极点，提供了pzmap函数绘制连续系统的零极点分布图。

b=[2,3,1];a=[1,2,2,1];
z=roots(b)
p=roots(a)
sys=tf(b,a);
pzmap(sys)

3．连续系统的频率响应

        若连续因果LTI连续系统的系统函数H(s)的极点全部位于S左半平面，则系统的频率响应可由H(s)求出：

MATLAB中freqs函数可以分析连续系统的频响，格式如下：

H=freqs(b,a,w): 计算系统在指定频率点向量w上的频响H；w为频率点向量。

[H,w]=freqs(b,a) : 自动选取200个频率点计算频率响应。

b=[1];  a=conv([1,1],[1,1,1]);
[H,w]=freqs(b,a);
plot(w,abs(H));
xlabel('Frequency(rad/s)');
ylabel('Amplitude');
title('Magnitude response');

4. 离散系统的时域响应

        离散时间LTI系统可用如下的线性常系数差分方程来描述：

  

        已知输入信号x[k]以及系统初始状态y[-1]，y[-2] ...，就可以求出系统的响应。MATLAB提供了计算差分方程的数值解的函数，可以计算上述差分方程描述的离散系统的单位脉冲响应、零状态响应和完全响应等。

        在调用MATLAB函数时，需要利用描述该离散系统的系数函数。对差分方程进行Z变换即可得系统函数：

        在MATLAB中可使用向量a和向量b分别保存分母多项式和分子多项式的系数：

    

这些系数均从z0按z的降幂排列。

(1) 离散系统的单位冲激响应h[k]的计算

[h,k] = impz(b, a)：计算系统的单位脉冲响应h[k]和相应的时间向量k；

也可简写为：h = impz(b, a)。
[h,k] = impz(b, a, n)：计算n点单位脉冲响应h[k]；

也可简写为：h = impz(b, a, n)。

impz(b, a)：绘制单位脉冲响应h[k]的图形。

(2) 离散系统响应y[k]的计算

y = filter(b, a, x)：计算系统在输入x作用下的零状态响应y[k]；

y = filter(b, a, x, zi)：计算系统在输入x和初始状态作用下的完全响应y[k]。

zi是由系统的初始状态经过filtic函数转换而得到的初始条件：zi= filtic (b, a, Y0) ，

Y0为系统的初始状态，Y0= [ y[-1]，y[-2]，y[-3]，...]。

5.离散系统的系统函数零极点分析

        离散LTI系统的系统函数H(z)可以表示为零极点形式使用MATLAB提供的roots函数计算离散系统的零极点；使用zplane函数绘制离散系统的零极点分布图。

        注意：在利用这些函数时，要求H(z)的分子多项式和分母多项式的系数的个数相等，若不等则需要补零。

b=[1,2,0];  
a=[1,0.4,-0.12];
z=roots(b)
p=roots(a)
zplane(b,a)

6.离散系统的频率响应

        当离散因果LTI系统的系统函数H(z)的极点全部位于z平面单位圆内时，系统的频率响应可由H(z)求出： 

[H, w]=freqz(b, a, n)： 计算系统的n点频率响应H，w为频率点向量：

(1)[H,w]=freqz(B,A,N);  %N默认值为512，区间默认0~pi

(2)[H,w]=freqz(B,A,N,'whole'); %区间默认-pi~pi

(3)[H,w]=freqz(B,A,[自定义区间]);

H=freqz(b, a, w) ：计算系统在指定频率点向量w上的频响；

a=1时相当于对b做傅里叶变换

freqz(b,a)： 绘制频率响应曲线。

其中：b和a分别为系统函数H(z)的分子分母系数矩阵；

b=[1,1];
a=[1,-1,0.5];
[H,w]=freqz(b,a);
plot(w,abs(H))
xlabel('Frequency(rad)');
ylabel('Magnitude');
title('Magnitude response');

7．利用DTFT和DFT确定离散系统的特性

        在很多情况下，需要根据LTI系统的输入和输出对系统进行辨识，即通过测量系统在已知输入x[k]激励下的响应y[k]来确定系统的特性。

        若系统的脉冲响应为h[k]，由于存在y[k]=x[k]* h[k]，因而可在时域通过解卷积方法求解h[k]，但进行信号解卷积比较困难。因此，通常从频域来分析系统，这样就可以将时域的卷积转变为频域的乘积，从而通过分析系统输入序列和输出序列的频率特性来确定系统的频率特性，再由得到系统的脉冲响应h[k]。

        有限长序列的DTFT可以利用FFT计算出其在区间内的N个等间隔频率点上的样点值：

X = fft(x,N);   Y = fft(y,N); 再利用 H = Y./X 和 h =  ifft(H,N) 可以得到系统的单位脉冲响应h[k]。