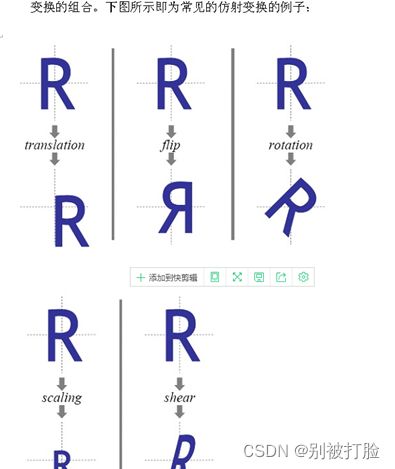
NNDL 实验五 前馈神经网络（1）二分类任务

目录

前言

一、4.1 神经元

4.1.1 净活性值

【思考题】加权相加与仿射变换之间有什么区别和联系？

4.1.2 激活函数

动手实现《神经网络与深度学习》4.1节中提到的其他激活函数：

4.2 基于前馈神经网络的二分类任务

4.2.1 数据集构建

4.2.2 模型构建

4.2.3 损失函数

4.2.4 模型优化

4.2.5 完善Runner类：RunnerV2_1

4.2.6 模型训练

4.2.7 性能评价

【思考题】对比

3.1 基于Logistic回归的二分类任务 4.2 基于前馈神经网络的二分类任务

修正与反思 

---

前言

   我这次还是写的非常细，但是这次学到很多东西，感觉都是值得的，同时，也有很多写的不太好的，希望老师，各位大佬帮我看看，多教教我。

---

       老师放的图，上课又讲了一下含义，必须给予足够的敬意，哈哈哈(确实在不同的时候学，能看到的东西是不一样的）  

一、4.1 神经元

4.1.1 净活性值

使用pytorch计算一组输入的净活性值z

净活性值z经过一个非线性函数f(·)后，得到神经元的活性值a

使用pytorch计算一组输入的净活性值，代码：

# coding=gbk
import torch
import matplotlib.pyplot as plt

 先说一下导入的包，这里注意的是，最好规定解码方式，也就是上边的#后边的，这样写注释才不会报错

# coding=gbk
import torch
import matplotlib.pyplot as plt
# 2个特征数为5的样本
X = torch.rand(size=[2, 5])

# 含有5个参数的权重向量
w = torch.rand(size=[5, 1])
# 偏置项
b = torch.rand(size=[1, 1])

# 使用'paddle.matmul'实现矩阵相乘
z = torch.matmul(X, w) + b
print("input X:", X)
print("weight w:", w, "\nbias b:", b)
print("output z:", z)

运行结果为：

input X: tensor([[0.2964, 0.5642, 0.3367, 0.5913, 0.9778],
        [0.6172, 0.4592, 0.1300, 0.5215, 0.6865]])
weight w: tensor([[0.5211],
        [0.6267],
        [0.7972],
        [0.3148],
        [0.9257]]) 
bias b: tensor([[0.4842]])
output z: tensor([[2.3520],
        [1.9969]])

       这个其实通过之前，对于函数理解就可以知道这个就是一个矩阵乘法 ，但是我要说的是，这个相当于适应全连接层，一般全连接的层的操作就是这样的，这个可以参考鱼书，鱼书上没用框架写全连接层大致就是这样的(细节上会有差异)。下文中的torch.nn.Linear,就是全连接层的意思，也证实了前边。

在飞桨中，可以使用nn.Linear完成输入张量的上述变换。

在pytorch中学习相应函数torch.nn.Linear(features_in, features_out, bias=False)。

实现上面的例子，完成代码，进一步深入研究torch.nn.Linear()的使用。

# coding=gbk
import torch
import matplotlib.pyplot as plt
#用torch.nn.Linear转写
m = torch.nn.Linear(5, 1)
output=m(X)
print("input X:", X)
print("weight w:", m.weight, "\nbias b:", m.bias)
print("output z:", output)
print(output.size())

运行结果为：

input X: tensor([[0.0437, 0.9488, 0.0253, 0.2438, 0.6656],
        [0.0254, 0.0952, 0.5115, 0.4278, 0.2640]])
weight w: Parameter containing:
tensor([[ 0.4026, -0.2537,  0.2964,  0.1648,  0.0925]], requires_grad=True) 
bias b: Parameter containing:
tensor([-0.2852], requires_grad=True)
output z: tensor([[-0.3991],
        [-0.0526]], grad_fn=)
torch.Size([2, 1])

先说一下函数的是啥意思，有啥用法

torch.nn.Linear(features_in, features_out, bias=False)

in_feature： int型, 在forward中输入Tensor最后一维的通道数

out_feature： int型, 在forward中输出Tensor最后一维的通道数

bias: bool型， Linear线性变换中是否添加bias偏置

这个解释一下就是，相当于自动生成了上一个代码段中的w和b，这个注意bias就是看要不要b的相当于，这个就是全连接层，同时输出属性时注意是，weight和bais属性就是上题中的w和b

它这个函数的意思就是输入，input的最后一层通道数，output的最后一层的通道数(输入、输出的第一层维度不变），这样就是生成了w和b，正好符合矩阵相乘的规则。(专门输出了一下形状，从形状中可以看出）

说完用法说一下，关联到的东西，这个经常要加一个，torch.autograd.variable这个，对数据进行这个处理，也就是自动微分求导，这时咱们以后搭框架常用的，这是经常写在一起的，后边就知道了。 

下边是官方文档，有兴趣的可以去看一看。

【思考题】加权相加与仿射变换之间有什么区别和联系？

首先，要明白它们之间的区别与联系，就要先明白，他们两个的定义，这时，老师发的那个就非常重要了，然后再结合我收集到的资料，来写一下(这个问题我真是第一次写，所以真的费了好大的劲，实在不想浪费了，所以可能东西有点多，这个会把链接放在下边了。)

这是百度给出的定义，在下边会用到这个 

这学期的神书蒲公英书上的：

 鱼书上的：

到这其实已经体现了部分核心的意思

神书蒲公英书上其实给了解释：

让我们再看看其它：

 

 并且我又查到了

1. 线性变换

线性变换有三个特点：

1. 变换前是直线，变换后依然是直线；
2. 直线比例保持不变
3. 变换前是原点，变换后依然是原点

2. 仿射变换

仿射变换有两个特点：

1. 变换前是直线，变换后依然是直线；
2. 直线比例保持不变

少了原点保持不变这一条

上边就已经体现他们的区别，也就是，通过线性变换来完成仿射变换

增加一个维度，就可以再高维度通过线性变换来完成低维度的仿射变换。(这个从百度的定义就可以看出）

这里先说一下，老师上课讲了之后，我理解的：

       在神经网络当中其实这两个就是一样的，因为从表达式就可以看出这两个表达式是一样的，这是从公式来，看这个是完全一样的(在神经网络当中)，这就体现了邱锡鹏大神数学上强大的能力。

       但是从定义上来看，如同下边的例子一样，加权相加只是乘以权重相加，而仿设变换会如同上边的图片中，我给出的定义中一样，它不仅会加权相加，在它的定义中还有类似于图像变换的操作(我查了一下，由于仿设变换就来源于图像的处理，所以它会带上这样的特性）

        总结一下，就是神经网络中这两个相等的，但是其他时候就不一定相等了，可以认为是在特定情况下的相等。因为从定义上来说，仿射变换的定义就比加权相加定义的要多。

4.1.2 激活函数

激活函数通常为非线性函数，可以增强神经网络的表示能力和学习能力。

常用的激活函数有S型函数和ReLU函数。

4.1.2.1 Sigmoid 型函数

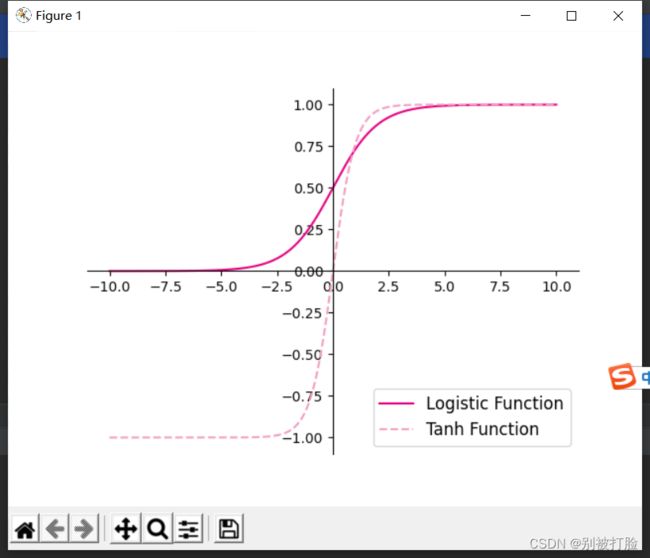
常用的 Sigmoid 型函数有 Logistic 函数和 Tanh 函数。

1. 使用python实现并可视化“Logistic函数、Tanh函数”

# coding=gbk
import torch
import matplotlib.pyplot as plt
# Logistic函数
def logistic(z):
    return 1.0 / (1.0 + torch.exp(-z))

# Tanh函数
def tanh(z):
    return (torch.exp(z) - torch.exp(-z)) / (torch.exp(z) + torch.exp(-z))

# 在[-10,10]的范围内生成10000个输入值，用于绘制函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), logistic(z).tolist(), color='#e4007f', label="Logistic Function")
plt.plot(z.tolist(), tanh(z).tolist(), color='#f19ec2', linestyle ='--', label="Tanh Function")

ax = plt.gca() # 获取轴，默认有4个
# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')

plt.savefig('fw-logistic-tanh.pdf')
plt.show()

运行结果为：

       这个其实就相当于是函数的调用，就是按照logistics函数和tanh函数的公式，来调用相应的数学函数来计算，我要说的是这个是其中的.tolist()，是将数据转化成列表，这也是我之前说过的转化方法，真的很好用。

     2.在飞桨中，可以通过调用paddle.nn.functional.sigmoid和paddle.nn.functional.tanh实现对张量的Logistic和Tanh计算。在pytorch中找到相应函数并测试。

      

# coding=gbk
import torch
import matplotlib.pyplot as plt
# 在[-10,10]的范围内生成10000个输入值，用于绘制函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), torch.sigmoid(z).tolist(), color='#e4007f', label="Logistic Function")
plt.plot(z.tolist(), torch.tanh(z).tolist(), color='#f19ec2', linestyle ='--', label="Tanh Function")

ax = plt.gca() # 获取轴，默认有4个
# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')

plt.savefig('fw-logistic-tanh.pdf')
plt.show()

运行结果为：

      这个一定要注意，一定要按上边的写法，这也是我之前看视频的时候，大佬们的常用的写法，如果用torch.nn.functional.sigmoid(z).tolist()和torch.nn.functional.tanh(z).tolist()的话，出现警告。也就是torch.nn.functional中也有这个函数，但是现在不太常用了。

      UserWarning: nn.functional.sigmoid is deprecated. Use torch.sigmoid instead.
  warnings.warn("nn.functional.sigmoid is deprecated. Use torch.sigmoid instead.")

     UserWarning: nn.functional.tanh is deprecated. Use torch.tanh instead.
  warnings.warn("nn.functional.tanh is deprecated. Use torch.tanh instead.")

        这个的意思是，方法快被弃用了，所以还是按我上边的写法，那样常见一点。 

4.1.2.2 ReLU型函数

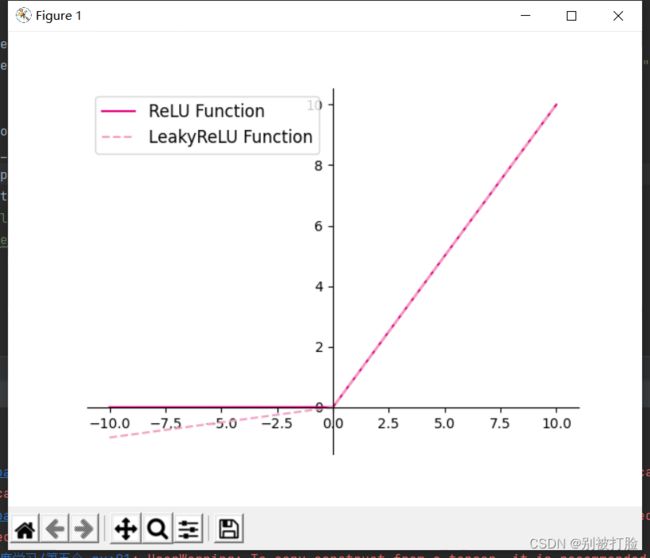
常见的ReLU函数有ReLU和带泄露的ReLU（Leaky ReLU）

1. 使用python实现并可视化可视化“ReLU、带泄露的ReLU的函数”

# coding=gbk
import torch
import matplotlib.pyplot as plt
# ReLU
def relu(z):
    return torch.maximum(z, torch.tensor(0.))

# 带泄露的ReLU
def leaky_relu(z, negative_slope=0.1):
    # 当前版本paddle暂不支持直接将bool类型转成int类型，因此调用了paddle的cast函数来进行显式转换
    a1 = (torch.tensor((z > 0), dtype=torch.float32) * z)
    a2 = (torch.tensor((z <= 0), dtype=torch.float32) * (negative_slope * z))
    return a1 + a2

# 在[-10,10]的范围内生成一系列的输入值，用于绘制relu、leaky_relu的函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), relu(z).tolist(), color="#e4007f", label="ReLU Function")
plt.plot(z.tolist(), leaky_relu(z).tolist(), color="#f19ec2", linestyle="--", label="LeakyReLU Function")

ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('fw-relu-leakyrelu.pdf')
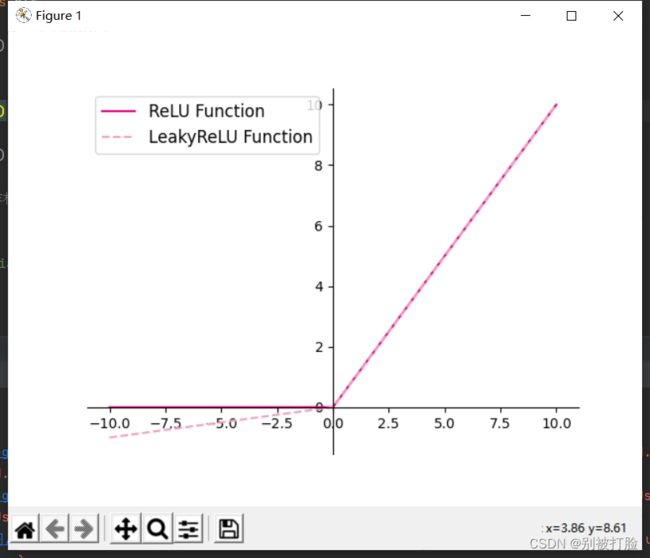
plt.show()

运行结果为：

这个也要报两个警告，

UserWarning: To copy construct from a tensor, it is recommended to use sourceTensor.clone().detach() or sourceTensor.clone().detach().requires_grad_(True), rather than torch.tensor(sourceTensor).

UserWarning: To copy construct from a tensor, it is recommended to use sourceTensor.clone().detach() or sourceTensor.clone().detach().requires_grad_(True), rather than torch.tensor(sourceTensor).

      但是这个没办法只能这么用了，因为之前我用的是像tensor.int()这种，如.float()、.double()。但是这次发现那么操作之后，发现用不了。只能用torch.tensor函数重新定义了，通过dtype实现了。

       这个注意的是，这个函数的意思是，那个判断是转化成bool类型，也就是Flase和Ture，但是转化为int类型后，也就是转化为0和1，所以后边要乘z，才能化为原来的数值大小。

     2.在飞桨中，可以通过调用paddle.nn.functional.relu和paddle.nn.functional.leaky_relu完成ReLU与带泄露的ReLU的计算。在pytorch中找到相应函数并测试。       

     

# coding=gbk
import torch
import matplotlib.pyplot as plt
# 在[-10,10]的范围内生成一系列的输入值，用于绘制relu、leaky_relu的函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), torch.relu(z).tolist(), color="#e4007f", label="ReLU Function")
plt.plot(z.tolist(), torch.nn.functional.leaky_relu(z,negative_slope=0.1).tolist(), color="#f19ec2", linestyle="--", label="LeakyReLU Function")

ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('fw-relu-leakyrelu.pdf')
plt.show()

运行结果为：

        这个如果按我上边的写法，并不会出现警告，因为在上像leaky_relu()这样的函数，只能是这个用法，如果用torch.nn.LeakyReLU()，这就是之前的生成迭代器的用法了，这样的不能直接带数进去，只能生成迭代器，然后来实现，并且这个方法并没有弃用。

        但是，正如我之前的说的，像relu这样的函数，最好还是用，torch直接调用，这是比较常见，同时说一下negative_slope=0.1，这个参数就是上边手写时候的参数，说直白的点就是偏离程度。

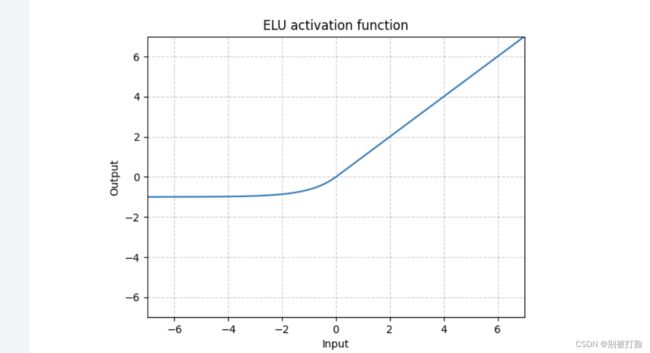
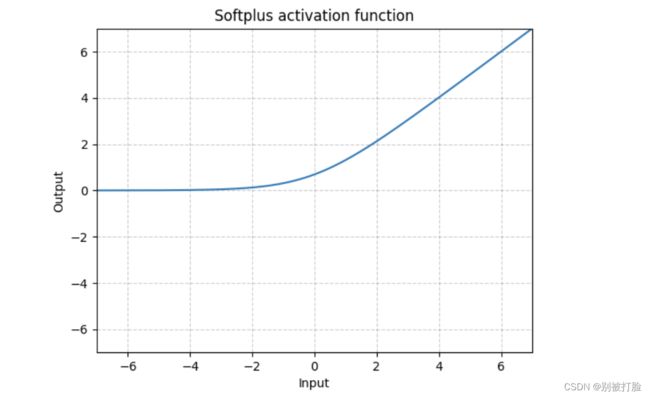
动手实现《神经网络与深度学习》4.1节中提到的其他激活函数：

Hard-Logistic、Hard-Tanh、ELU、Softplus、Swish等。（选做）

为了方便理解我用的nn里边的，但是正常的要用nn.functional里边的

这个一定要查一查官方文档

然后，我先把官方文档的截图放在这，再放函数图像，这个要是就是稍微改改函数，就没什么意义了

 

4.2 基于前馈神经网络的二分类任务

4.2.1 数据集构建

使用第3.1.1节中构建的二分类数据集：Moon1000数据集，其中训练集640条、验证集160条、测试集200条。该数据集的数据是从两个带噪音的弯月形状数据分布中采样得到，每个样本包含2个特征。

from nndl import make_moons
# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.5)

num_train = 640
num_dev = 160
num_test = 200

X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]

y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])

这个需要用到的函数为(这个需要在中创建或者在之前的nndl函数中，添加make_moons函数)：

# coding=gbk
import torch
import math
def make_moons(n_samples=1000, shuffle=True, noise=None):
    """
    生成带噪音的弯月形状数据
    输入：
        - n_samples：数据量大小，数据类型为int
        - shuffle：是否打乱数据，数据类型为bool
        - noise：以多大的程度增加噪声，数据类型为None或float，noise为None时表示不增加噪声
    输出：
        - X：特征数据，shape=[n_samples,2]
        - y：标签数据, shape=[n_samples]
    """
    n_samples_out = n_samples // 2
    n_samples_in = n_samples - n_samples_out

    # 采集第1类数据，特征为(x,y)
    # 使用'paddle.linspace'在0到pi上均匀取n_samples_out个值
    # 使用'paddle.cos'计算上述取值的余弦值作为特征1，使用'paddle.sin'计算上述取值的正弦值作为特征2
    outer_circ_x = torch.cos(torch.linspace(0, math.pi, n_samples_out))
    outer_circ_y = torch.sin(torch.linspace(0, math.pi, n_samples_out))

    inner_circ_x = 1 -torch.cos(torch.linspace(0, math.pi, n_samples_in))
    inner_circ_y = 0.5 - torch.sin(torch.linspace(0, math.pi, n_samples_in))

    print('outer_circ_x.shape:', outer_circ_x.shape, 'outer_circ_y.shape:', outer_circ_y.shape)
    print('inner_circ_x.shape:', inner_circ_x.shape, 'inner_circ_y.shape:', inner_circ_y.shape)

    # 使用'paddle.concat'将两类数据的特征1和特征2分别延维度0拼接在一起，得到全部特征1和特征2
    # 使用'paddle.stack'将两类特征延维度1堆叠在一起
    X = torch.stack(
        [torch.cat([outer_circ_x, inner_circ_x]),
         torch.cat([outer_circ_y, inner_circ_y])],
        dim=1
    )

    print('after concat shape:', torch.cat([outer_circ_x, inner_circ_x]).shape)
    print('X shape:', X.shape)

    # 使用'paddle. zeros'将第一类数据的标签全部设置为0
    # 使用'paddle. ones'将第一类数据的标签全部设置为1
    y = torch.cat(
        [torch.zeros(size=[n_samples_out]), torch.ones(size=[n_samples_in])]
    )

    print('y shape:', y.shape)

    # 如果shuffle为True，将所有数据打乱
    if shuffle:
        # 使用'paddle.randperm'生成一个数值在0到X.shape[0]，随机排列的一维Tensor做索引值，用于打乱数据
        idx = torch.randperm(X.shape[0])
        X = X[idx]
        y = y[idx]

    # 如果noise不为None，则给特征值加入噪声
    if noise is not None:
        # 使用'paddle.normal'生成符合正态分布的随机Tensor作为噪声，并加到原始特征上
        X += torch.normal(mean=0.0, std=noise, size=X.shape)

    return X, y

 代码的思想为：

       这个就像是之前的，思想一样，只不过是用了一步函数的调用，就是前边几个根据变量名就是相应的训练集，测试集，验证集，然后用了一些切片的操作划分了一下。

注意一点，nndl.dataset是nndl文件夹下的dataset文件，这个一定要注意。

4.2.2 模型构建

为了更高效的构建前馈神经网络，我们先定义每一层的算子，然后再通过算子组合构建整个前馈神经网络。

4.2.2.1 线性层算子

# 实现线性层算子
class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=torch.randn, bias_init=torch.zeros):
        """
        输入：
            - input_size：输入数据维度
            - output_size：输出数据维度
            - name：算子名称
            - weight_init：权重初始化方式，默认使用'paddle.standard_normal'进行标准正态分布初始化
            - bias_init：偏置初始化方式，默认使用全0初始化
        """

        self.params = {}
        # 初始化权重
        self.params['W'] = weight_init(size=(input_size, output_size))
        # 初始化偏置
        self.params['b'] = bias_init(size=[1, output_size])
        self.inputs = None

        self.name = name

    def forward(self, inputs):
        """
        输入：
            - inputs：shape=[N,input_size], N是样本数量
        输出：
            - outputs：预测值，shape=[N,output_size]
        """
        self.inputs = inputs

        outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs
class Logistic(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None

    def forward(self, inputs):
        """
        输入：
            - inputs: shape=[N,D]
        输出：
            - outputs：shape=[N,D]
        """
        outputs = 1.0 / (1.0 + torch.exp(-inputs))
        self.outputs = outputs
        return outputs

4.2.2.2 Logistic算子（激活函数）

class Logistic(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None

    def forward(self, inputs):
        """
        输入：
            - inputs: shape=[N,D]
        输出：
            - outputs：shape=[N,D]
        """
        outputs = 1.0 / (1.0 + torch.exp(-inputs))
        self.outputs = outputs
        return outputs

4.2.2.3 层的串行组合

# 实现一个两层前馈神经网络
class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        """
        输入：
            - input_size：输入维度
            - hidden_size：隐藏层神经元数量
            - output_size：输出维度
        """
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

    def __call__(self, X):
        return self.forward(X)

    def forward(self, X):
        """
        输入：
            - X：shape=[N,input_size], N是样本数量
        输出：
            - a2：预测值，shape=[N,output_size]
        """
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2

代码的大体思想：

       这个是那三个算子，这个其实就有点相当于是，上边咱们已经拿函数实现过主要的过程了，这次是拿类封装的方式再写一遍。

但是这个要注意，上边在Linear当中，标准正太分布函数函数最好用randn实现，并且记住，不要在后边加()，并且最好不要用torch.nn.Embedding.weight(num_embeddings, embedding_dim)，因为这个已经被弃用但是，是已经启用不是上边说的将要弃用。

下边是调用和调试代码

# 实例化模型
model = Model_MLP_L2(input_size=5, hidden_size=10, output_size=1)
# 随机生成1条长度为5的数据
X = torch.rand(size=[1, 5])
result = model(X)
print ("result: ", result)

运行结果为：

result:  tensor([[0.8532]]) 

代码的大体思想：

        这个的其实就是函数和类的调用，注意类的初始化的就行了(这个在之前是说过的）。

4.2.3 损失函数

二分类交叉熵损失函数见第三章

# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(Op):
    def __init__(self, model):
        self.predicts = None
        self.labels = None
        self.num = None

        self.model = model

    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        """
        输入：
            - predicts：预测值，shape=[N, 1]，N为样本数量
            - labels：真实标签，shape=[N, 1]
        输出：
            - 损失值：shape=[1]
        """
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = -1. / self.num * (torch.matmul(self.labels.t(), torch.log(self.predicts))
                                 + torch.matmul((1 - self.labels.t()), torch.log(1 - self.predicts)))

        loss = torch.squeeze(loss, axis=1)
        return loss

      这个建议大家保留一下这个封装，这个封装真的是非常常用，而且非常实用的，这个是大家都这么写，只是在这个基础上改，所以非常重要 。

4.2.4 模型优化

神经网络的层数通常比较深，其梯度计算和上一章中的线性分类模型的不同的点在于：

线性模型通常比较简单可以直接计算梯度，而神经网络相当于一个复合函数，需要利用链式法则进行反向传播来计算梯度。

4.2.4.1 反向传播算法

1. 第1步是前向计算，可以利用算子的forward()方法来实现；
2. 第2步是反向计算梯度，可以利用算子的backward()方法来实现；
3. 第3步中的计算参数梯度也放到backward()中实现，更新参数放到另外的优化器中专门进行。

4.2.4.2 损失函数

二分类交叉熵损失函数

实现损失函数的backward()

# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(Op):
    def __init__(self, model):
        self.predicts = None
        self.labels = None
        self.num = None

        self.model = model

    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        """
        输入：
            - predicts：预测值，shape=[N, 1]，N为样本数量
            - labels：真实标签，shape=[N, 1]
        输出：
            - 损失值：shape=[1]
        """
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = -1. / self.num * (torch.matmul(self.labels.t(), torch.log(self.predicts))
                                 + torch.matmul((1 - self.labels.t()), torch.log(1 - self.predicts)))

        loss = torch.squeeze(loss, axis=1)
        return loss

    def backward(self):
        # 计算损失函数对模型预测的导数
        loss_grad_predicts = -1.0 * (self.labels / self.predicts -
                                     (1 - self.labels) / (1 - self.predicts)) / self.num

        # 梯度反向传播
        self.model.backward(loss_grad_predicts)

代码的大体思想： 

     这个是真正的交叉损失函数的封装了，这个连backward(也就是反向传播)都有了，所以非常建议大家来看看这个，好好理解理解这个，这解释上回就解释过， 增加的反向传播技术，想求损失函数的导数，然后按照，来进行迭代。

4.2.4.3 Logistic算子

为Logistic算子增加反向函数

class Logistic(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None
        self.params = None

    def forward(self, inputs):
        outputs = 1.0 / (1.0 + torch.exp(-inputs))
        self.outputs = outputs
        return outputs

    def backward(self, grads):
        # 计算Logistic激活函数对输入的导数
        outputs_grad_inputs = torch.multiply(self.outputs, (1.0 - self.outputs))
        return torch.multiply(grads,outputs_grad_inputs)

代码的大体思想：

       这个其实和上边说的函数是差不多，但是多了一个反向传播，其实反向传播思想就是上边说的反向传播的思想，只是把变量换了，但是都是那个思想。 

4.2.4.4 线性层

线性层输入的梯度

计算线性层参数的梯度

class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=torch.rand, bias_init=torch.zeros):
        self.params = {}
        self.params['W'] = weight_init(size=[input_size, output_size])
        self.params['b'] = bias_init(size=[1, output_size])

        self.inputs = None
        self.grads = {}

        self.name = name

    def forward(self, inputs):
        self.inputs = inputs
        outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs

    def backward(self, grads):
        """
        输入：
            - grads：损失函数对当前层输出的导数
        输出：
            - 损失函数对当前层输入的导数
        """
        self.grads['W'] = torch.matmul(self.inputs.T, grads)
        self.grads['b'] = torch.sum(grads, axis=0)

        # 线性层输入的梯度
        return torch.matmul(grads, self.params['W'].T)

 代码的大体思想：

        这个其实就是前边写过的那个函数，相当于都是升级了一下，加了一个反向传播，思想其实都是前边我说过的那个。

4.2.4.5 整个网络

实现完整的两层神经网络的前向和反向计算

class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        # 线性层
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        # Logistic激活函数层
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

        self.layers = [self.fc1, self.act_fn1, self.fc2, self.act_fn2]

    def __call__(self, X):
        return self.forward(X)

    # 前向计算
    def forward(self, X):
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2

    # 反向计算
    def backward(self, loss_grad_a2):
        loss_grad_z2 = self.act_fn2.backward(loss_grad_a2)
        loss_grad_a1 = self.fc2.backward(loss_grad_z2)
        loss_grad_z1 = self.act_fn1.backward(loss_grad_a1)
        loss_grad_inputs = self.fc1.backward(loss_grad_z1)

 代码的大体思想：

        这个其实就是前边写过的那个函数，相当于都是升级了一下，加了一个反向传播，思想其实都是前边我说过的那个。

4.2.4.6 优化器

在计算好神经网络参数的梯度之后，我们将梯度下降法中参数的更新过程实现在优化器中。

与第3章中实现的梯度下降优化器SimpleBatchGD不同的是，此处的优化器需要遍历每层，对每层的参数分别做更新。

from opitimizer import Optimizer
class BatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(BatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        # 参数更新
        for layer in self.model.layers: # 遍历所有层
            if isinstance(layer.params, dict):
                for key in layer.params.keys():
                    layer.params[key] = layer.params[key] - self.init_lr * layer.grads[key]

       这个是优化器的函数，我一般喜欢把优化的函数归归类，所以，优化器的函数，写都在一起，下边是这次需要到的(这个是我那个总的优化器文件，这次就用到了其中的一个)。

# coding=gbk
import torch

from abc import abstractmethod
def optimizer_lsm(model, X, y, reg_lambda=0):
    """
      输入：
         - model: 模型
         - X: tensor, 特征数据，shape=[N,D]
         - y: tensor,标签数据，shape=[N]
         - reg_lambda: float, 正则化系数，默认为0
      输出：
         - model: 优化好的模型
      """

    N, D = X.shape

    # 对输入特征数据所有特征向量求平均
    x_bar_tran = torch.mean(X, dim=0).T

    # 求标签的均值,shape=[1]
    y_bar = torch.mean(y)

    # paddle.subtract通过广播的方式实现矩阵减向量
    x_sub = torch.subtract(X, x_bar_tran)

    # 使用paddle.all判断输入tensor是否全0
    if torch.all(x_sub == 0):
        model.params['b'] = y_bar
        model.params['w'] = torch.zeros(size=[D])
        return model

    # paddle.inverse求方阵的逆
    tmp = torch.inverse(torch.matmul(x_sub.T, x_sub) +
                         reg_lambda * torch.eye((D)))

    w = torch.matmul(torch.matmul(tmp, x_sub.T), (y - y_bar))

    b = y_bar - torch.matmul(x_bar_tran, w)

    model.params['b'] = b
    model.params['w'] = torch.squeeze(w, dim=-1)

    return model

#新增优化器基类
class Optimizer(object):
    def __init__(self, init_lr, model):

        #初始化学习率，用于参数更新的计算
        self.init_lr = init_lr
        #指定优化器需要优化的模型
        self.model = model

    @abstractmethod
    def step(self):
        pass

      这个要注意是另外再创一个文件，不要写在一起。

4.2.5 完善Runner类：RunnerV2_1

1. 支持自定义算子的梯度计算，在训练过程中调用self.loss_fn.backward()从损失函数开始反向计算梯度；
2. 每层的模型保存和加载，将每一层的参数分别进行保存和加载。

import os
class RunnerV2_1(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []

        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []

    def train(self, train_set, dev_set, **kwargs):
        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)

        # 传入模型保存路径
        save_dir = kwargs.get("save_dir", None)

        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)  # return a tensor

            self.train_loss.append(trn_loss.item())
            # 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)

            self.loss_fn.backward()

            # 参数更新
            self.optimizer.step()

            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
                if save_dir:
                    self.save_model(save_dir)

            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")

    def evaluate(self, data_set):
        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss

    def predict(self, X):
        return self.model(X)

    def save_model(self, save_dir):
        # 对模型每层参数分别进行保存，保存文件名称与该层名称相同
        for layer in self.model.layers:  # 遍历所有层
            if isinstance(layer.params, dict):
                torch.save(layer.params, os.path.join(save_dir, layer.name + ".pdparams"))

    def load_model(self, model_dir):
        # 获取所有层参数名称和保存路径之间的对应关系
        model_file_names = os.listdir(model_dir)
        name_file_dict = {}
        for file_name in model_file_names:
            name = file_name.replace(".pdparams", "")
            name_file_dict[name] = os.path.join(model_dir, file_name)

        # 加载每层参数
        for layer in self.model.layers:  # 遍历所有层
            if isinstance(layer.params, dict):
                name = layer.name
                file_path = name_file_dict[name]
                layer.params = torch.load(file_path)

代码的大体思想：     

       这个其实就是搭整个训练模型得过程，这个过程我在你当初神经网络预测鸢尾花的时候，就是这个流程，但是当时没有以类的方式封装，这个调用是很好的，思想大家可以看看我之前的鸢尾花那，也就是那个选做，那是很详细的。

4.2.6 模型训练

使用训练集和验证集进行模型训练，共训练2000个epoch。评价指标为accuracy。

torch.manual_seed(123)
epoch_num = 2000

model_saved_dir = "model"

# 输入层维度为2
input_size = 2
# 隐藏层维度为5
hidden_size = 5
# 输出层维度为1
output_size = 1

# 定义网络
model = Model_MLP_L2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)

# 损失函数
loss_fn = BinaryCrossEntropyLoss(model)

# 优化器
learning_rate = 0.2
optimizer = BatchGD(learning_rate, model)

# 评价方法
metric = accuracy

# 实例化RunnerV2_1类，并传入训练配置
runner = RunnerV2_1(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_dir=model_saved_dir)

               这个记得，在当前文件夹下创建一个玩文件夹”model“ 

 epoch=2000，lr=0.2的时候：

[Train] epoch: 50/2000, loss: 0.6209933161735535
[Train] epoch: 100/2000, loss: 0.5517048239707947
[Train] epoch: 150/2000, loss: 0.4977870583534241
[Train] epoch: 200/2000, loss: 0.4655247628688812
[Train] epoch: 250/2000, loss: 0.4473403990268707
[Train] epoch: 300/2000, loss: 0.4369833171367645
[Train] epoch: 350/2000, loss: 0.43102437257766724
[Train] epoch: 400/2000, loss: 0.42759305238723755
[Train] epoch: 450/2000, loss: 0.4256167411804199
[Train] epoch: 500/2000, loss: 0.4244685769081116
[Train] epoch: 550/2000, loss: 0.423786461353302
[Train] epoch: 600/2000, loss: 0.42336463928222656
[Train] epoch: 650/2000, loss: 0.42308807373046875
[Train] epoch: 700/2000, loss: 0.42289334535598755
[Train] epoch: 750/2000, loss: 0.4227454364299774
[Train] epoch: 800/2000, loss: 0.4226253926753998
[Train] epoch: 850/2000, loss: 0.4225224554538727
[Train] epoch: 900/2000, loss: 0.42243075370788574
[Train] epoch: 950/2000, loss: 0.4223468005657196
[Train] epoch: 1000/2000, loss: 0.42226916551589966
[Train] epoch: 1050/2000, loss: 0.4221959710121155
[Train] epoch: 1100/2000, loss: 0.42212677001953125
[Train] epoch: 1150/2000, loss: 0.4220612645149231
[Train] epoch: 1200/2000, loss: 0.4219990670681
[Train] epoch: 1250/2000, loss: 0.4219396710395813
[Train] epoch: 1300/2000, loss: 0.42188262939453125
[Train] epoch: 1350/2000, loss: 0.42182818055152893
[Train] epoch: 1400/2000, loss: 0.4217758774757385
[Train] epoch: 1450/2000, loss: 0.42172566056251526
[Train] epoch: 1500/2000, loss: 0.4216773211956024
[Train] epoch: 1550/2000, loss: 0.4216306805610657
[Train] epoch: 1600/2000, loss: 0.4215858578681946
[Train] epoch: 1650/2000, loss: 0.4215422570705414
[Train] epoch: 1700/2000, loss: 0.4215005040168762
[Train] epoch: 1750/2000, loss: 0.42145976424217224
[Train] epoch: 1800/2000, loss: 0.4214206337928772
[Train] epoch: 1850/2000, loss: 0.42138242721557617
[Train] epoch: 1900/2000, loss: 0.42134523391723633
[Train] epoch: 1950/2000, loss: 0.42130914330482483

 epoch=2000，lr=0.2的时候：

[Train] epoch: 0/2000, loss: 0.9169712066650391
[Train] epoch: 50/2000, loss: 0.8151296973228455
[Train] epoch: 100/2000, loss: 0.7524362802505493
[Train] epoch: 150/2000, loss: 0.7154122591018677
[Train] epoch: 200/2000, loss: 0.6937174201011658
[Train] epoch: 250/2000, loss: 0.6806467175483704
[Train] epoch: 300/2000, loss: 0.6722604632377625
[Train] epoch: 350/2000, loss: 0.6663665771484375
[Train] epoch: 400/2000, loss: 0.661780834197998
[Train] epoch: 450/2000, loss: 0.6578733325004578
[Train] epoch: 500/2000, loss: 0.6543120741844177
[Train] epoch: 550/2000, loss: 0.6509205102920532
[Train] epoch: 600/2000, loss: 0.6476064324378967
[Train] epoch: 650/2000, loss: 0.644320011138916
[Train] epoch: 700/2000, loss: 0.6410347819328308
[Train] epoch: 750/2000, loss: 0.6377367377281189
[Train] epoch: 800/2000, loss: 0.634417712688446
[Train] epoch: 850/2000, loss: 0.6310743689537048
[Train] epoch: 900/2000, loss: 0.6277047991752625
[Train] epoch: 950/2000, loss: 0.6243082880973816
[Train] epoch: 1000/2000, loss: 0.6208862662315369
[Train] epoch: 1050/2000, loss: 0.6174390912055969
[Train] epoch: 1100/2000, loss: 0.6139692068099976
[Train] epoch: 1150/2000, loss: 0.6104788780212402
[Train] epoch: 1200/2000, loss: 0.6069709062576294
[Train] epoch: 1250/2000, loss: 0.6034483909606934
[Train] epoch: 1300/2000, loss: 0.5999146699905396
[Train] epoch: 1350/2000, loss: 0.5963738560676575
[Train] epoch: 1400/2000, loss: 0.5928294658660889
[Train] epoch: 1450/2000, loss: 0.589285671710968
[Train] epoch: 1500/2000, loss: 0.5857465267181396
[Train] epoch: 1550/2000, loss: 0.5822162628173828
[Train] epoch: 1600/2000, loss: 0.5786991119384766
[Train] epoch: 1650/2000, loss: 0.5751994252204895
[Train] epoch: 1700/2000, loss: 0.5717212557792664
[Train] epoch: 1750/2000, loss: 0.5682684183120728
[Train] epoch: 1800/2000, loss: 0.5648452043533325
[Train] epoch: 1850/2000, loss: 0.561454713344574
[Train] epoch: 1900/2000, loss: 0.5581009984016418
[Train] epoch: 1950/2000, loss: 0.554787278175354

 epoch=1000，lr=0.2的时候：

[Train] epoch: 0/1000, loss: 0.9169712066650391
[Train] epoch: 50/1000, loss: 0.6209933161735535
[Train] epoch: 100/1000, loss: 0.5517048239707947
[Train] epoch: 150/1000, loss: 0.4977870583534241
[Train] epoch: 200/1000, loss: 0.4655247628688812
[Train] epoch: 250/1000, loss: 0.4473403990268707
[Train] epoch: 300/1000, loss: 0.4369833171367645
[Train] epoch: 350/1000, loss: 0.43102437257766724
[Train] epoch: 400/1000, loss: 0.42759305238723755
[Train] epoch: 450/1000, loss: 0.4256167411804199
[Train] epoch: 500/1000, loss: 0.4244685769081116
[Train] epoch: 550/1000, loss: 0.423786461353302
[Train] epoch: 600/1000, loss: 0.42336463928222656
[Train] epoch: 650/1000, loss: 0.42308807373046875
[Train] epoch: 700/1000, loss: 0.42289334535598755
[Train] epoch: 750/1000, loss: 0.4227454364299774
[Train] epoch: 800/1000, loss: 0.4226253926753998
[Train] epoch: 850/1000, loss: 0.4225224554538727
[Train] epoch: 900/1000, loss: 0.42243075370788574
[Train] epoch: 950/1000, loss: 0.4223468005657196

从上边就可以看出，其实大约在1000轮左右的时候损失就会降低的十分不明显了，但是lr取0.01是，会发现损失暴增，由此可见，lr=0.01，并不是适合所有情况，这个确实是我的误区了。 

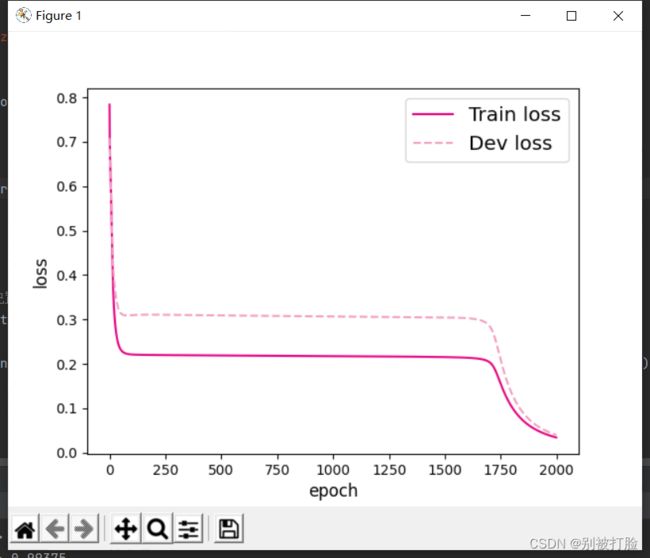
# 打印训练集和验证集的损失
plt.figure()
plt.plot(range(epoch_num), runner.train_loss, color="#e4007f", label="Train loss")
plt.plot(range(epoch_num), runner.dev_loss, color="#f19ec2", linestyle='--', label="Dev loss")
plt.xlabel("epoch", fontsize='large')
plt.ylabel("loss", fontsize='large')
plt.legend(fontsize='x-large')
plt.savefig('fw-loss2.pdf')
plt.show()

 运行结果为：

4.2.7 性能评价

# 加载训练好的模型
runner.load_model(model_saved_dir)
# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])

print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

运行结果为：

[Test] score/loss: 0.7600/0.4912 

       这里要注意之前说过的路径问题，否则真的会修改好久 

import math
# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-math.pi, math.pi, 200), torch.linspace(-math.pi, math.pi, 200))
x = torch.stack([torch.flatten(x1), torch.flatten(x2)], axis=1)

# 预测对应类别
y = runner.predict(x)
y = torch.squeeze(torch.tensor((y>=0.5),dtype=torch.float32),axis=-1)

# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:,0].tolist(), x[:,1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)

plt.scatter(X_train[:, 0].tolist(), X_train[:, 1].tolist(), marker='*', c=torch.squeeze(y_train,axis=-1).tolist())
plt.scatter(X_dev[:, 0].tolist(), X_dev[:, 1].tolist(), marker='*', c=torch.squeeze(y_dev,axis=-1).tolist())
plt.scatter(X_test[:, 0].tolist(), X_test[:, 1].tolist(), marker='*', c=torch.squeeze(y_test,axis=-1).tolist())

plt.show()

运行结果为：

代码的大体思想：

        这个其实就是验证一下模型，但是从划分结果来看，就可以初步的就看出前馈神经网络的优越性，但是建议最好还是自己动手搭一个网络，从鱼书上看，或这自己尝试着用numpy写，就像我之前发的那个iris分类。 

【思考题】对比

3.1 基于Logistic回归的二分类任务 4.2 基于前馈神经网络的二分类任务

谈谈自己的看法

首选，先说一下，我的理解：

       第一点，肯定是神经网络相对较好，但是为什么，这次相差不大，因为数据量的问题(这个问题第三点要吐槽一下)，因为人们肯定会朝着好的方向发展，所以一般情况下都会是神经网络较好，但是这只是普通的前馈神经网络，并且网络层也不深，所以不会相差太大。

      第二点，但是logistics回归是相对来说，迭代过程没有这么复杂的，也不会出现这次的存储和取出的问题(这个真是要吐槽一下),所以数据量不是太大时，推荐logistics回归，这个是真的计算简单，并且求导啥的都方便(手写一次就知道了，拿numpy写真的相差太大了，用框架写体现不出来），从我之前发神经网络分类鸢尾花的就可以看出相差多少。

     第三点就是，这次建模中我用的就是logistics回归，用神经网络的话，就60个数据集，误差大的离谱，真的难受，这就是我说的数据集的问题，当数据集小时，推荐logistics回归，当数据集大时，推荐神经网络。

     

总结

        这次真的学到了好多，之前的话，我用numpy也写过前馈神经网络，我用框架也写过，可是我写的并不规范，都是想咋写，咋写，一点也不规范，这是必须要说的感受，规范真的很重要，好多回去看一眼都不能看明白(不规范的话)。

        第一部分是，感觉后边的基础，这一部分学了好多函数封装好的写法，之前写的时候大多是调库，并没有这么规范过，用numpy写的没有写过这些函数。这些感觉真是学到了好多，并且真的明白了pytorch文档的重要性，以前从来没感觉pytorch文档，这么方便，这次查了好多函数，学到了，这个学习方法感觉是最重要的，授人以鱼不如授人以渔，哈哈哈

       第二部分是，感觉是把第一部分的基础，实践一下，也就是实战，这一部分感觉学到了好多，路径的问题，解决了半天才解决了，一开始模型存不进去，后来解决了，这并且调参那方面，终于明白了自己的误区，并不是所有的lr调成0.001就好，这两次的实验，调成0.001都是不好的。

      最后是当然是感谢老师，哈哈哈

修正与反思

      

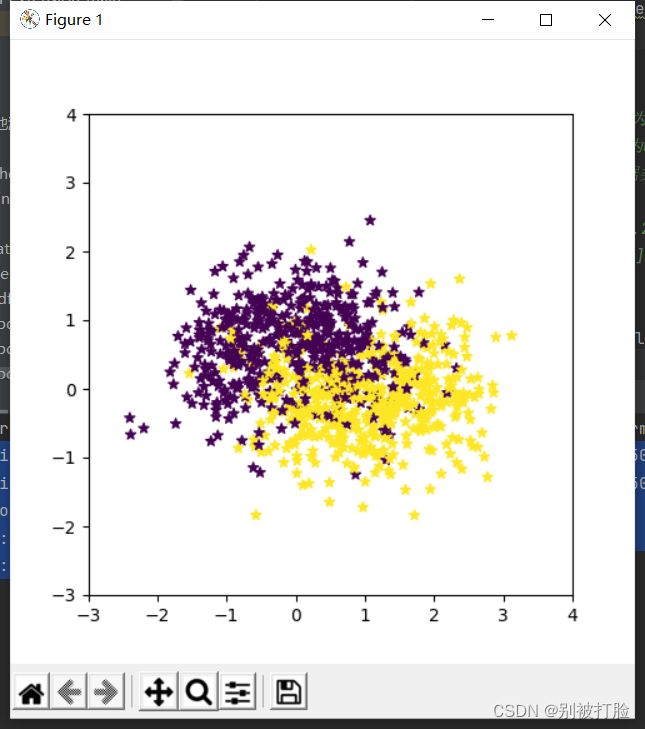
      经过这次的反思，确实学到了很多，包括对学习率的考虑，以及对过拟合和欠拟合的考虑，首先，先说一下遇到了什么问题，在一开始的弯月数据集上测试，根本无法体现神经网络的特性，也就是对于下边这样的数据集，无论是线性还是非线性，都无法很好的对它进行分类。

       

       在这样的数据集下，运用神经网络对其分类，和运用logistics回归对其分类，出来的结果，都是以一条直线对其分类，虽然作为分类准则的那条线并不是一条，但是这样并不能体现出神经网络对非线性的情况进行处理的特性，也就是，根本无法体现出神经网络的优越性。

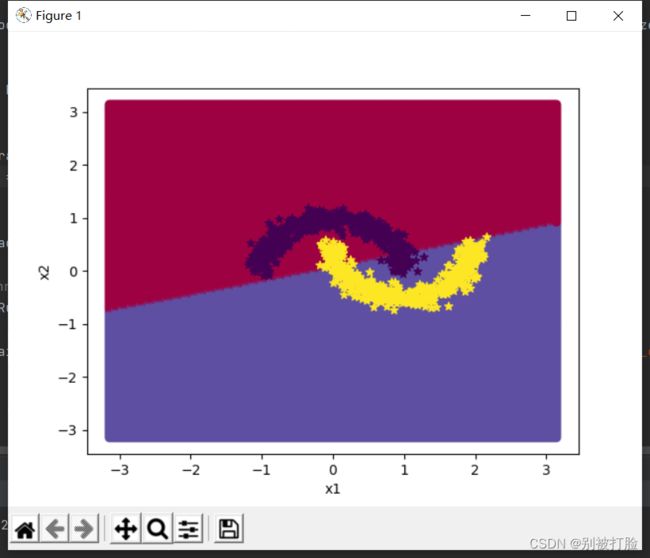
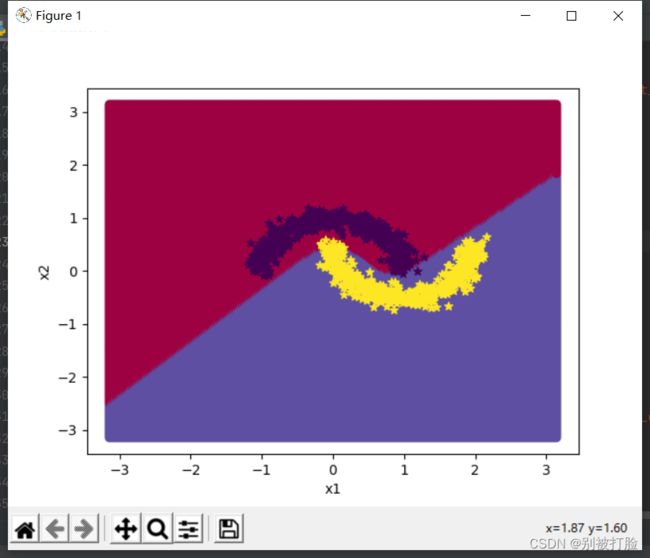
        从下边的图片对比中，就可以看出几乎相差不大，如果不是准确率和损失有变化的话，还以为是一条曲线。（第一张为logistics回归，第二张为神经网络，损失函数图像一样）

         用logistics回归来进行的时：

            用神经网络来进行分类时：

 

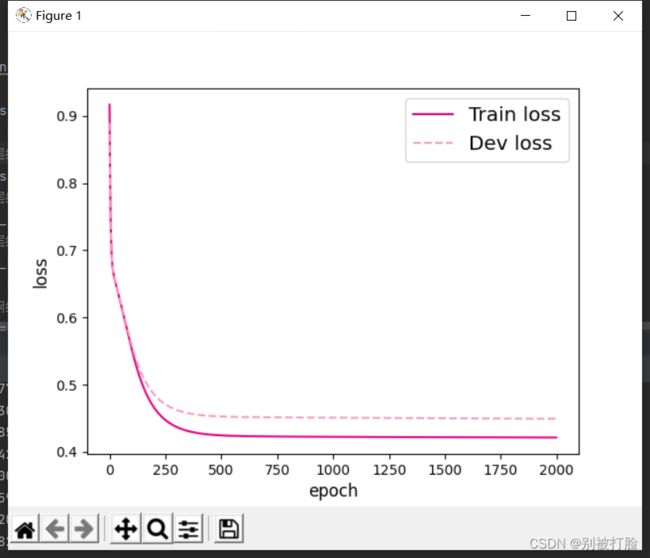         其实从这个就可以大概看出，两个模型的优劣，但是这并没有体现出神经网络的优越性。

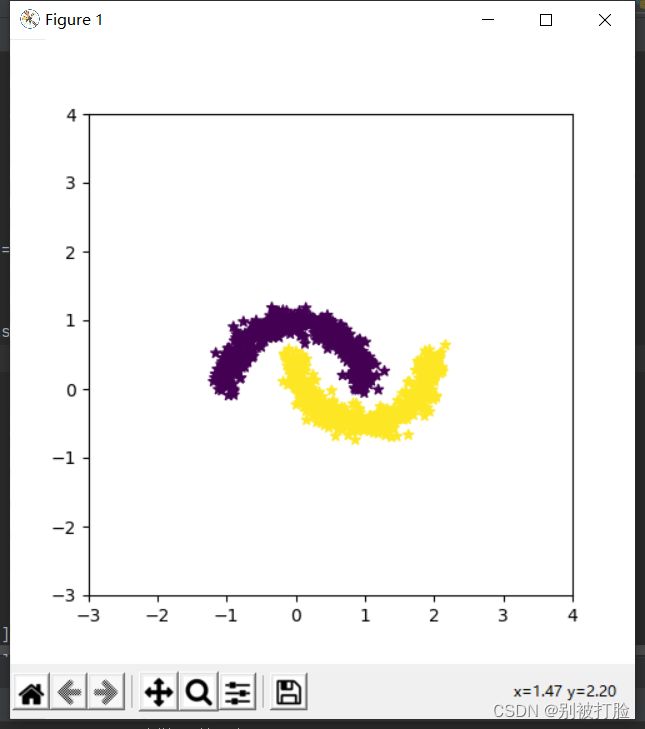
     所以我们将数据集进行如下更改(对noise进行更改,将其变得不那么离散)：

# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.1)

图像为：

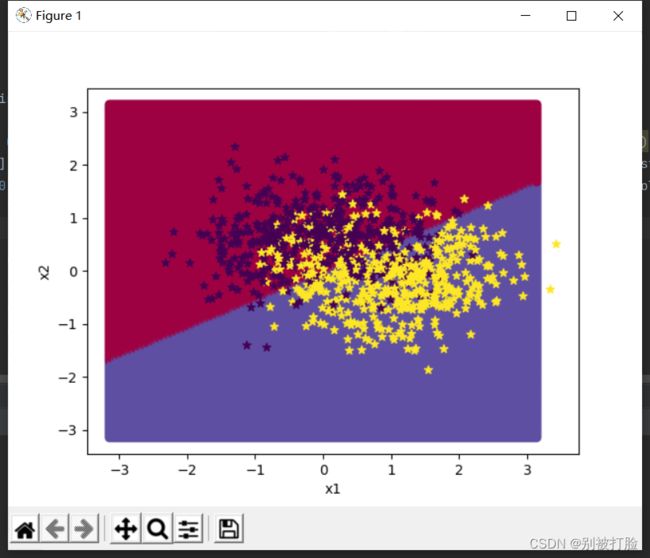
        这样的，函数，明显是可分的，但是不是线性可分，这时神经网络的优越性就能完美的体现出来了。

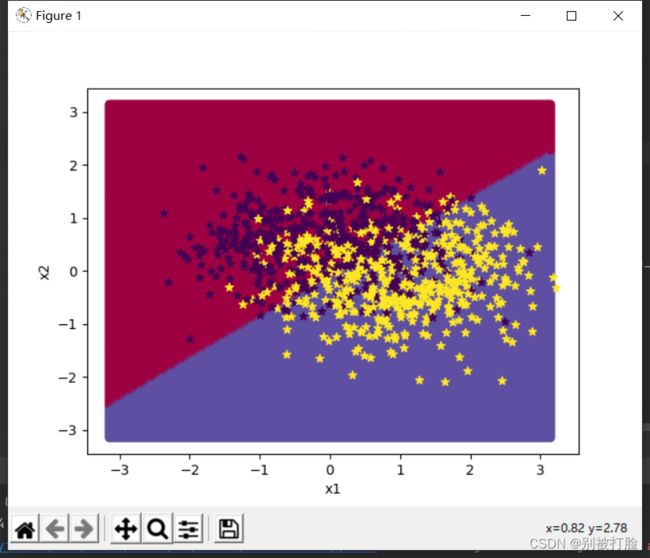
       咱们用事实说话，看logistics回归和神经网络各自体现出来的图像和准确率。

       用logistics回归进行分类的图像：

       用神经网络进行分类的图像：

       从上边的图中，就可以完美的看出哪个好了，神经网络的损失，最后都趋于零了，这样就可以体现出神经网络非线性的特征的强大之处

       这里必须要说一点，在修正的时候遇到的问题了，问了老师好多才明白了，所以必须要写一下。（经验主义害死人）

       首先，说下学习率的问题，大家不要用写经典网络的经验，来判断所以，这个学习率本质上是跟着训练集来的，不要用经验主义来做判断，来调试，应该像老师说的大胆的去调试。就大胆的去调试，大胆的试，不要想着什么0.01啥的，就按当前的网络来说，这个，虽然我前边也注意的到过，但是没有足够的重视，这次终于在这研究了半天，问了问老师才明白。

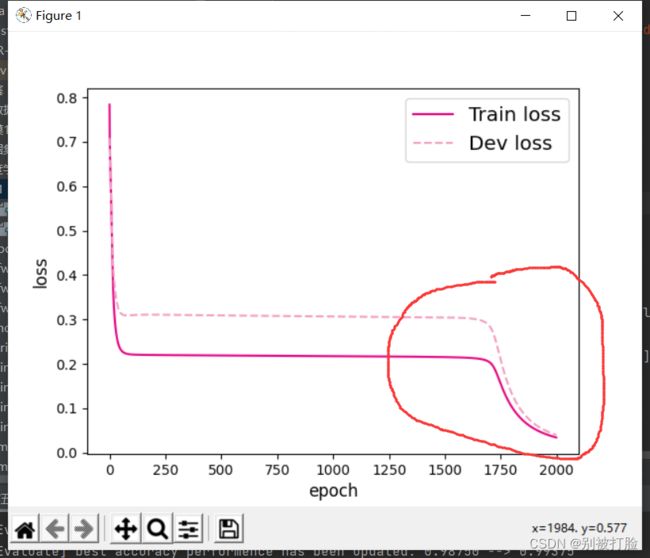
       然后说一下，过拟合和欠拟合的问题，这个其实最好的办法就是，按照定义来分析，这个在最后我会给出定义，咱们现在来说一下分析的时候，好多人遇见损失长时间不变，然后突然减小趋于零，这种情况大多数时候确实是过拟合了，这种判断的方法，好多博客或者网课为了简便都说过这种判断方法，但是就像下面这种情况，就不行了。    

      像这种情况，我一开始也是坚信它过拟合了，后来问了问，老师，想了想，这种简单的数据集，它很有可能是遇见了局部极小值，然后在迭代了一段时间之后，可能跳出了局部极小值，学习到了全部的特征后，从而到达了全局极小点，这样就会出现这种情况(确实是我考虑少了，呜呜 )

       最后，在这里给大家说一下，过拟合和欠拟合的定义，大家最好还是按照定义来判断，这样才不会错。

        过拟合（Overfitting）：就是太过贴近于训练数据的特征了，在训练集上表现非常优秀，近乎完美的预测/区分了所有的数据，但是在新的测试集上却表现平平，不具泛化性，拿到新样本后没有办法去准确的判断。

        欠拟合（UnderFitting）：测试样本的特性没有学到，或者是模型过于简单无法拟合或区分样本。

        所以，大家判断的时候，还是向老师给我说的，在验证集上试一试就知道了，这样才是判断的唯一标准，也就是实践是检验真理的唯一标准，大家一定不要经验主义。

        最后，改这个改了两天，感觉这次把所有的问题都要考虑到了，弄了好长时间，大家看着这个一步一步调就调出来了。

        虽然时间长但是感觉都是值得的，真的学了好多东西，明白了好多误区。

        最后感谢老师的帮助，谢谢老师。