【图像处理matlab】PCA+KNN人脸识别 ORL人脸数据集

0.写在前面

本实验使用ORL数据集中的前100张人脸图像进行

实验整体思路为：

1. PCA数据降维，使用train图片计算映射脸空间，以实现将每张人脸的二维灰度图矩阵降维至一维的点
2. 欧式距离，求出某张映射后test图片到所有映射后train图片的欧式距离
3. KNN分类，2步骤求出的所有距离值升序排列，取最小前k个（k自定义），出现频数最多的label为test图片的预测类别
4. 验证并计算准确率

1. 数据集导入与划分

首先应明确以下几点：

• 数据集大小为100
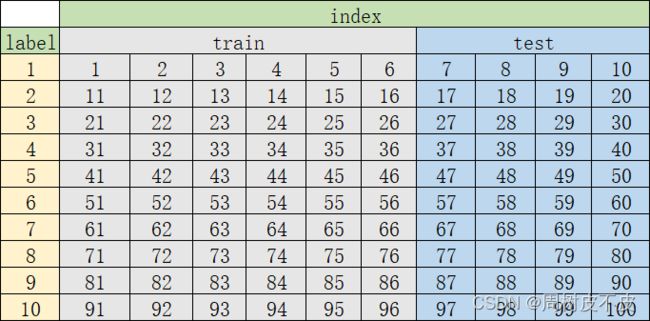
• 每行10张，为一个人的全部图像。共10人
• 数据集的60%为训练集，40%为测试集。以实现交叉验证
  
  接着：
• 按照上图的排序对100张图片进行编号
• 每个人对应label标签1-10
• 每个人的前6张作为train训练集，后4张作为test测试集

经上述步骤，可将数据集结构抽象为下表：

接下来基于上表结构，介绍如何使用matlab实现数据集的导入与划分

1. 导入

• （1）dir函数
  dataset=dir（‘path\ *.类型’）以读取指定文件夹path下的指定类型的全部文件

实验中图片均为.bmp格式，使用如下语句获取每张图片的信息：

list_names=dir('C:\Users\ZKX\Desktop\ORL_100\*.bmp') 

得到一个100*1的结构体，记录了每张图片的如下信息

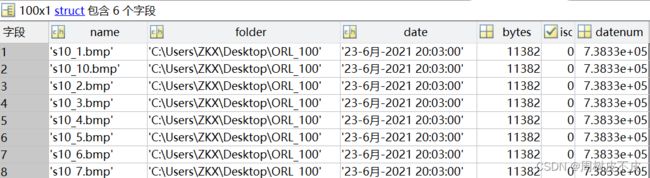
创建以下变量

• img_num：记录数据集大小
• folder：记录存储数据集文件夹路径

方便后续imread的导入

img_num = length(list_names);% 文件夹中图像的个数
folder=list_names.folder

• （2）imread函数
  imread（‘path\文件名’）以读取指定图片

其中：

1）path由上一步folder获得
2）文件名由上一步结构体变量list_names(idx).name获得
3）idx下标范围为1-数据集大小img_num

在matlab中使用[str1,str2,…]进行字符串拼接，故每张图片imread路径可表示为：‘path\文件名’=[folder,’ \ '，list_names(idx).name]

构造DB矩阵存储所有图片的灰度值矩阵，可通过如下语句实现：

DB= zeros(112,92,img_num);
for idx = 1:img_num
    DB(:,:,idx)  =imread([folder,'\',list_names(idx).name]);%读取图像数据,类似构建mat矩阵
end

DB = reshape(DB, 112*92,100);

查看用于存储100张图片灰度值的变量DB

• 像素数：10304= heigh * weigh=112 * 92
• 图像总数:100张

2. 划分
   

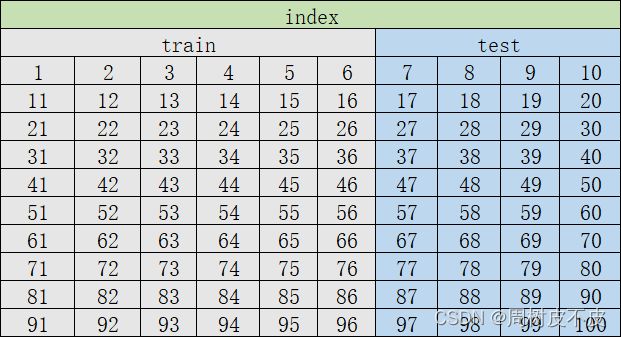
观察发现：
训练集图片的下标以1、2、3、4、5、6结尾
测试集图片的下标以7、8、9、0结尾

数学归纳为：
test_data_index = 10* i+1:10* i+4
train_data_index =10* i+5:10* (i+1)

得到下标后，创建test_data、train_data ，利用下标读取DB进行划分存储。具体代码实现为：

%% train与test划分

% 取出前40%作为测试数据，剩下60%作为训练数据
test_data_index = [];
train_data_index = [];

%记录测试集和训练集的下标
for i=0:9
    test_data_index = [test_data_index 10*i+1:10*i+4];
    train_data_index = [train_data_index 10*i+5:10*(i+1)];
end

test_data = DB(:, test_data_index);
train_data = DB(:,train_data_index);

2. train-PCA构建脸空间

应明确PCA求解脸空间只是对train训练集的操作

首先回忆PCA算法步骤

S1：原始样本数据获取
S2：去中心化
S3：求解协方差矩阵
S4: 求取协方差矩阵的特征值和特征向量
S5 :排列特征值，最大特征值作为主成分w
S6：将特征值最大的d个向量作为投影向量，构成d*d维的投影矩阵W，
	对于任意维样本，将其投影选取的特征向量（主成分方向）上。

接下来对应上述步骤进行图像处理

2.1 原始数据导入

该步骤在上一节已经实现，现使用imshow函数测试部分导入图片显示是否正常

显示结果如下：

2.2 去中心化

• 求平均脸

  这里需明确，平均脸是对整个train求平均，最终得到一个10304x1的矩阵mean_face，以记录平均脸各像素点的灰度值。
  
  平均脸展示：
  
  可以看到，平均脸只能看出大致的人脸轮廓，而面部细节十分模糊

• 去中心化
  将train中的原始图片减去平均脸，也就是将train_data的每个列向量都减去列向量mean_face，得到去中心化的列向量centered_face
  
  
  将centered_face用imshow函数显示就是去中心化的人脸。由于每张图像都在原始灰度值的基础上减去了平均值，图像整体灰度值较原始降低，直观感受就是图片变暗。
  去中心化脸展示：
  

2.3 求解协方差矩阵、特征值、特征向量

数学知识，略

2.4 特征脸选取–脸空间

首先应明确特征脸的概念。特征脸就是一组特征向量的线性组合，特征量组数少的特征脸计算量少，特征量组数大的特征脸保留了更多的有效信息，权衡二者权重，实现在尽量保留图像原始信息的情况下降低计算量。
重构的特征脸就是Y=W*X中的W,即投影矩阵，在这里称为脸空间。

代码中的all_eigen_face代表所有的特征向量，也就是sorted_eigen_vectors

eigen_faces在实验中是分别选取10、20、30、·······100个特征值进行重构

将经过降序排序处理后的特征值sorted_eigen_vectors的前100个取出后发现：idx==60之后的数值已经小到可以忽略。即前60个特征量之和已接近总特征量之和，故使用前60个特征值重构的特征脸已经几乎接近原图。

下图展示分别选取10、20、30、······100个特征值重构的特征脸，直观感受是：随着特征量的增加，重构特征脸的细节越清晰。

到这里，实验已经实现了使用train计算映射脸空间，接下来要对test进行分类识别并计算分类正确率。

步骤为：

1. 将100张人脸投影到脸空间中进行降维，将每张人脸的二维灰度值矩阵降至一维的一个点
2. 欧几里得距离计算未知人脸（test中单张）与所有已知人脸（train全部）的距离
3. KNN分类预测标签

PCA选取特征脸部分介绍推荐该文：PCA实现人脸识别

3. test-物以类聚 KNN分类

首先了解一下大致分类：
机器学习与深度学习——关系、无/半/有监督学习、差异、主流框架

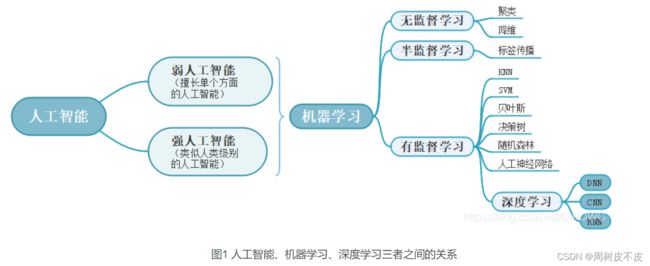
本实验对测试集的分类是使用有监督学习的KNN分类算法

有监督学习的主要特性是使用大量有标签的训练数据来建立模型，以预测新的未知标签的数据

该特性在实验KNN分类中体现为：使用训练数据计算脸空间后将全体数据降维，计算单个test最近的k个train，k个train中标签出现频数最多的为该test预测标签

3.1 KNN简介

算法的核心思想为：给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中

3.2 KNN实现步骤

影响KNN分类结果的因素有：

• 距离公式的选取
• k值的选取

3.2.1 距离度量—欧式距离、豪斯多夫距离…

本实验使用欧式距离，因为已经降维至坐标点，用初中学到的两点间距离公式即可：

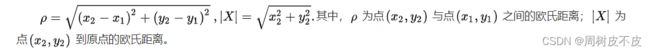
其他高端的距离公式

3.2.2 k值选择

KNN算法选取过小的k值,会使得模型变得复杂,容易过拟合,学习到的类别一般是噪声点,当选择过大的k值,会使得模型变得简单,相当于模型没有进行训练,可以理解为欠拟合。

KNN算法中是根据通过实验调参来得到,李航老师书上讲到，我们一般选取一个较小的数值，通常采取交叉验证法来选取最优的k值.

总结以上两段废话，k值选择可以摆烂凭经验（xs），或是在设置k值前沐浴焚香更衣
阿弥

k值选择影响/估计误差/近似误差介绍

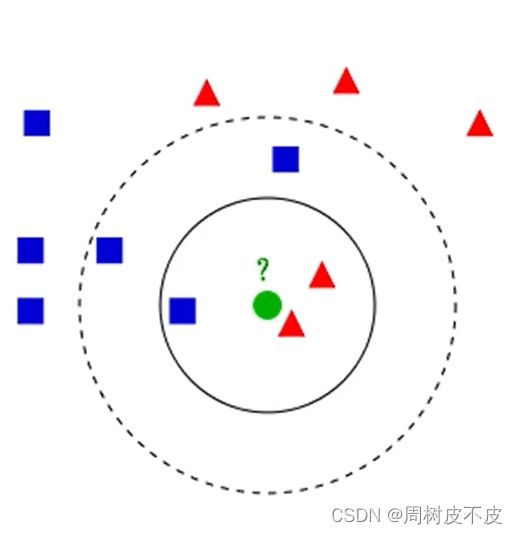
接下来用下图实例分析一下为什么不同的k值会对分类结果产生影响

珍珠预测小绿的类别

• 当k=3时
  距小绿最近的3个登西为：1小蓝+2小红
  故此时小绿一眼顶真为小红
• 当k=5时
  距小绿最近的5个登西为：3小蓝+2小红
  此时小绿跳小蓝

3.2.3 “投票”预测分类

涉及到一个标签与下标的转化，再度拿出让我蠢蠢欲动的结构图

用仅有的小学数学知识推导下标与label的关系：

  real_label = floor((test_data_index(1,each_test_face_index) - 1) / 10)+1;

最后用mode函数看k中出现最多的标签作为预测便签

  predict_label = mode(label_of_minimun_k_values);

结束捏

4. 结果分析

测试条件：

• 特征脸：特征量选择在[0，100]，步长为10
• k：基于每轮特征脸，k值选择在[1,6]，步长为1

测试输出：

• 对于每个样本
  将预测标签（KNN分类获得）的值与实际标签（自身下标转化）的值进行判断。

  若相等，输出：预测值：label，实际值:label，正确
  并将记录正确分类数目的correct_predict_number 加1

  若不等，输出：预测值：label，实际值:label，错误

代码实现如下：

   if (predict_label == real_label)
                fprintf("预测值：%d，实际值:%d，正确\n",predict_label,real_label);
                correct_predict_number = correct_predict_number + 1;
            else
                fprintf("预测值：%d，实际值:%d，错误\n",predict_label,real_label);

在命令行中显示为：

• 每轮内循环输出
  特征量固定，即特征脸确定的情况下输出6个k值的预测结果。输出包括：总测试量、正确数、正确率的信息。

   fprintf("k=%d，numOfeig=%d，总测试样本：%d，正确数:%d，正确率：%1f \n", k, i,test_face_number,correct_predict_number,correct_rate);

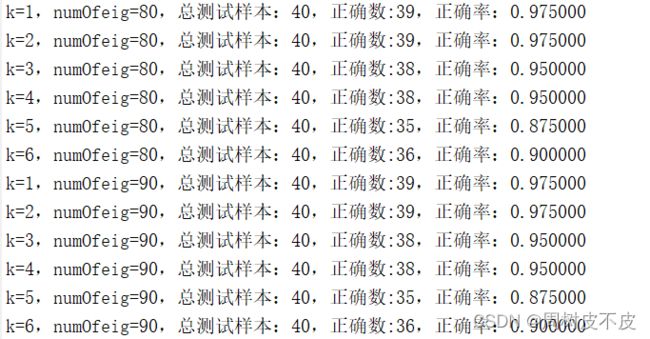
当特征值分别选为80、90两轮循环的结果在命令行中显示为：

全过程可视化结果展示：

5. matlab代码实现

clear all;

%% 数据导入
list_names=dir('C:\Users\ZKX\Desktop\ORL_100\*.bmp') 
img_num = length(list_names);% 文件夹中图像的个数
folder=list_names.folder

DB= zeros(112,92,img_num);

for idx = 1:img_num
    DB(:,:,idx)  =imread([folder,'\',list_names(idx).name]);%读取图像数据,类似构建mat矩阵
end

DB = reshape(DB, 112*92,100);

%% train与test划分

% 取出前40%作为测试数据，剩下60%作为训练数据
test_data_index = [];
train_data_index = [];

%记录测试集和训练集的下标
for i=0:9
    test_data_index = [test_data_index 10*i+1:10*i+4];
    train_data_index = [train_data_index 10*i+5:10*(i+1)];
end

test_data = DB(:, test_data_index);
train_data = DB(:,train_data_index);

waitfor(show_faces(train_data));


%% PCA算法实现

% S1：去中心化

%   1）求所有图像各像素点的平均值，即平均脸
mean_face = mean(train_data, 2); %计算出的是h*w的一张图，即平均脸
waitfor(show_face(mean_face));

%   2) 原始数据-mean，中心化每一列是一个一张图
centered_face = (train_data - mean_face);
waitfor(show_faces(centered_face));

% S2: 协方差矩阵的特征值与特征向量
%   1）cov协方差矩阵
cov_matrix = centered_face * centered_face';
[eigen_vectors, dianogol_matrix] = eig(cov_matrix);

%   2）特征值
eigen_values = diag(dianogol_matrix);

%   特征值降序排序，获得取特征值及其对应索引
[sorted_eigen_values, index] = sort(eigen_values, 'descend'); 

%   3）特征向量
sorted_eigen_vectors = eigen_vectors(:, index);

%% 特征脸(所有）

all_eigen_faces = sorted_eigen_vectors;

%% 特征脸选取

    %根据自己设定percent选出特征脸
    %根据选取特征量的数量构造特征脸
    
    %选出的特征脸就是W 
    %w*x就是映射到脸空间
    
    %正确的

%取出第一张人脸，使用不同数量的特征向量进行重构
single_face = centered_face(:,1);

index = 1;
X = [];
Y = [];

%下图是分别在10，20，30，…，100数量的特征向量下重构的人脸。
%从直观上可以看出随着特征向量数量的增加，重构出的人脸越来越清晰。
%这是因为使用越多的特征向量进行人脸重构，丢失的信息越少，因此重构出的人脸更加清晰。

numOfeig = 100   %特征值的数量

for i=10:10:numOfeig

    % 取出相应数量特征脸
    eigen_faces = all_eigen_faces(:,1:i);

    % 重建人脸并显示
    if (mod(i,10)==0)
        rebuild_faces = eigen_faces * (eigen_faces' * single_face) + mean_face;
        %%%
        subplot(2, 5, index);
        index = index + 1;
        fig = show_face(rebuild_faces);
        title(sprintf("i=%d", i));    

        if (i == 100)
            waitfor(fig);
        end
    end

 %% 测试、训练数据降维

 %计算不同数量特征向量下，人脸的识别准确度
 % 1）Y=W*X进行脸空间的映射
 % 2）使用欧式距离计算test与已知脸的距离
 % 3) 使用最近邻分类器KNN进行识别
 

 %projected_x_data就是降维后的reduced_face
    projected_train_data = eigen_faces' * (train_data - mean_face);
    projected_test_data = eigen_faces' * (test_data - mean_face);

    % KNN的k值
    %k就是人脸的标签判定数组的大小，出现最多次的就判断为true_label
    for k=1:6
        fprintf('knn')
        % 用于保存最小的k个值的矩阵
        % 用于保存最小k个值对应的人标签的矩阵
        minimun_k_values = zeros(k,1);
        label_of_minimun_k_values = zeros(k,1);

        % 测试脸的数量
        test_face_number = size(projected_test_data, 2);

        % 识别正确数量
        correct_predict_number = 0;

        % 遍历每一个待测试人脸
        for each_test_face_index = 1:test_face_number

            each_test_face = projected_test_data(:,each_test_face_index);
            
         %这边操作看似多余，其实是为了首先用6个值填满，减少之后空循环迭代
            for each_train_face_index = 1:k    
                %minimun_k_values 记录两点间距离 6*1矩阵
                minimun_k_values(each_train_face_index,1) = norm(each_test_face - projected_train_data(:,each_train_face_index));
                %label_of_minimun_k_values 就是通过计算算出实际的标签 -1 2 3 4 5 6 
                %label_of_minimun_k_values=[40,25;5,25;3,40]
                label_of_minimun_k_values(each_train_face_index,1) = floor((train_data_index(1,each_train_face_index) - 1) / 10) + 1;
            end

            % 找出k个值中最大值及其下标
            % IDX=5 
            [max_value, index_of_max_value] = max(minimun_k_values);

            % 计算与剩余每一个已知人脸的距离
            for each_train_face_index = k+1:size(projected_train_data,2)

                % 计算距离
                %norm函数就是求欧式距离
                distance = norm(each_test_face - projected_train_data(:,each_train_face_index));

                % 遇到更小的距离就更新距离和标签
                if (distance < max_value)
                    minimun_k_values(index_of_max_value,1) = distance;
                    label_of_minimun_k_values(index_of_max_value,1) = floor((train_data_index(1,each_train_face_index) - 1) / 10) + 1;
                    [max_value, index_of_max_value] = max(minimun_k_values);
                end
            end

            % 最终得到距离最小的k个值以及对应的标签
            % 取出出现次数最多的值，为预测的人脸标签
            
            %标签和下标的关系为： label=floor((train_data_index(1,each_train_face_index) - 1) / 10) + 1
            predict_label = mode(label_of_minimun_k_values);
            real_label = floor((test_data_index(1,each_test_face_index) - 1) / 10)+1;

            if (predict_label == real_label)
                fprintf("预测值：%d，实际值:%d，正确\n",predict_label,real_label);
                correct_predict_number = correct_predict_number + 1;
            else
                fprintf("预测值：%d，实际值:%d，错误\n",predict_label,real_label);
            end
        end

        %正确率
        correct_rate = correct_predict_number/test_face_number;

        X = [X k];
        Y = [Y correct_rate];
        
        fprintf("k=%d，numOfeig=%d，总测试样本：%d，正确数:%d，正确率：%1f \n", k, i,test_face_number,correct_predict_number,correct_rate);

    end
end

waitfor(plot(X,Y));

%% 功能函数 图像可视化

% 输入向量，显示脸

function fig = show_face(vector)
    fig= imshow((reshape(vector, [112 92]))/255);
end

% 显示矩阵中某些脸
function fig = show_faces(eigen_vectors)
    count = 1;
    index_of_image_to_show = [1,5,10,15,20,25,30,35];
    for i=index_of_image_to_show
        subplot(2,4,count);
        fig = show_face(eigen_vectors(:, i));
        title(sprintf("i=%d", i));
        count = count + 1;
    end
end

参考

特征脸法原理及代码讲解
代码参考
KNN原理介绍1
KNN原理介绍2