K-means聚类的实现以及案例讲解

目录

 

1 k-means聚类步骤

2. 案例联系

3. K-means的api初步使用

3.1 api 介绍

​

4. 案列

4.1 流程分析

4.2 代码实现

4.3 完整代码

4.4 实验结果

---

1 k-means聚类步骤

 

• 1、 随机设置K个特征空间内的点作为初始的聚类中⼼
• 2、 对于其他每个点计算到K个中⼼的距离， 未知的点选择最近的⼀个聚类中⼼点作为标记类别
• 3、 接着对着标记的聚类中⼼之后， 重新计算出每个聚类的新中⼼点（平均值）
• 4、 如果计算得出的新中⼼点与原中⼼点⼀样（质⼼不再移动） ， 那么结束， 否则重新进⾏第⼆步过程

通过下图解释实现流程：

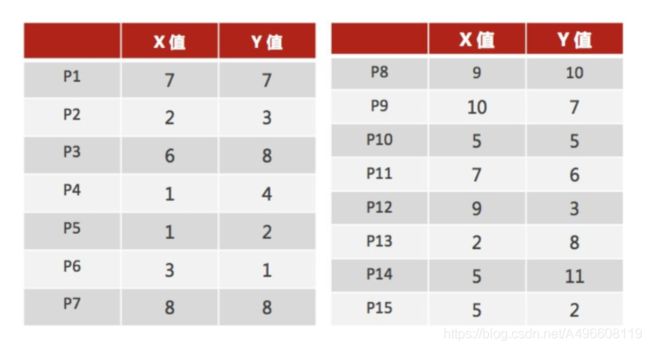
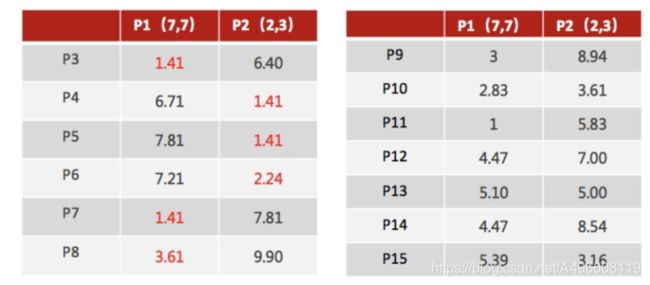
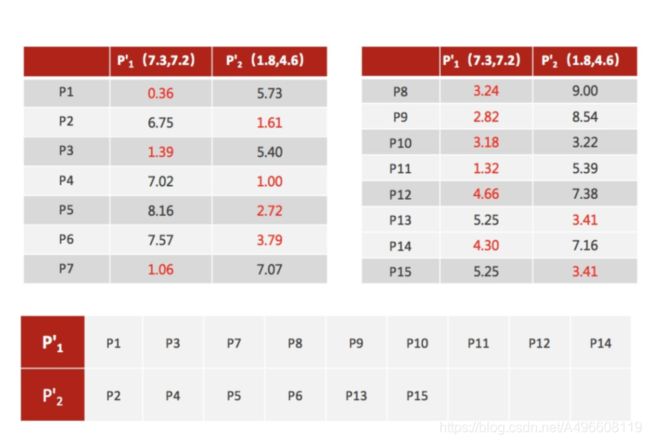
2. 案例联系

1、 随机设置K个特征空间内的点作为初始的聚类中⼼（本案例中设置p1和p2）

2、 对于其他每个点计算到K个中⼼的距离， 未知的点选择最近的⼀个聚类中⼼点作为标记类别
 

3、 接着对着标记的聚类中⼼之后， 重新计算出每个聚类的新中⼼点（平均值）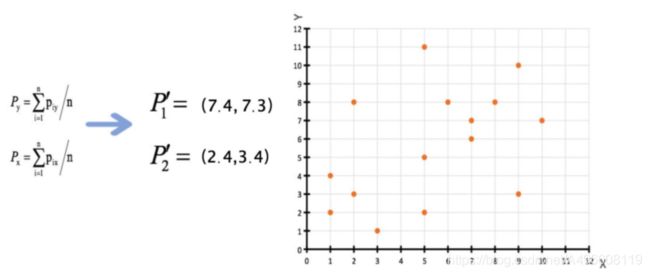

4、 如果计算得出的新中心点与原中⼼点⼀样（质⼼不再移动） ， 那么结束， 否则重新进⾏第⼆步过程【经过判断， 需
要重复上述步骤， 开始新⼀轮迭代。

5、 当每次迭代结果不变时， 认为算法收敛， 聚类完成， K-Means⼀定会停下， 不可能陷⼊⼀直选质⼼的过程。

3. K-means的api初步使用

3.1 api 介绍

4. 案列

随机创建不同⼆维数据集作为训练集， 并结合k-means算法将其聚类， 你可以尝试分别聚类不同数量的簇， 并观察聚类
效果：                                                                                                         聚类参数n_cluster传值不同， 得到的聚类结果不同

4.1 流程分析

4.2 代码实现

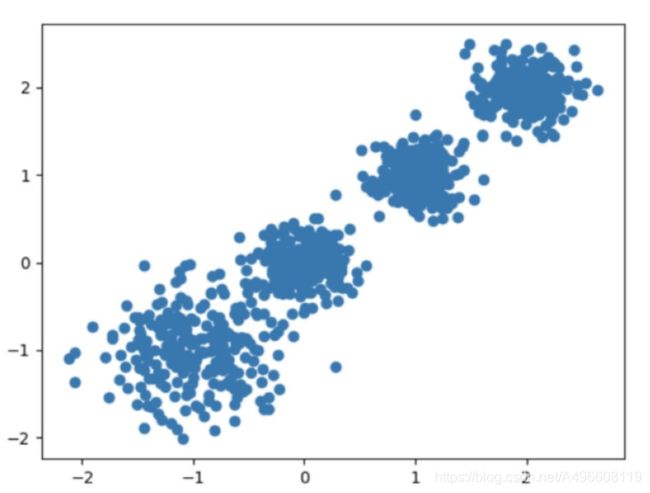
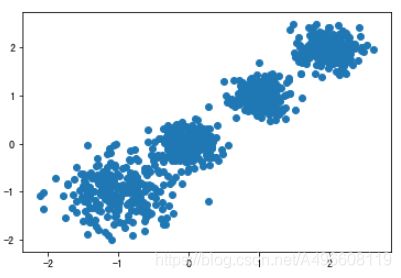
1. 创建数据集

import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import calinski_harabaz_score
# 创建数据集
# X为样本特征， Y为样本簇类别， 共1000个样本， 每个样本2个特征， 共4个簇，
# 簇中⼼在[-1,-1], [0,0],[1,1], [2,2]， 簇⽅差分别为[0.4, 0.2, 0.2, 0.2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
cluster_std=[0.4, 0.2, 0.2, 0.2],
random_state=9)
# 数据集可视化
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()

2.使用K-means进行聚类，并使用CH 方法进行评估

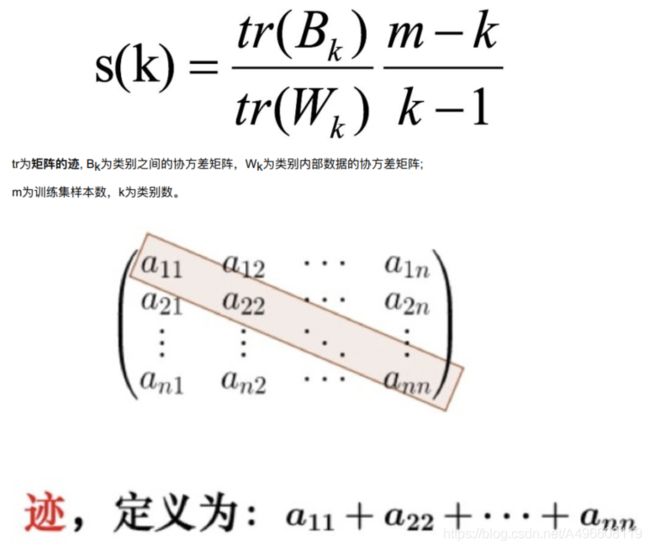
CH 系数（Calinski-Harabasz Index

类别内部数据的协⽅差越⼩越好， 类别之间的协⽅差越⼤越好（换句话说： 类别内部数据的距离平⽅和越⼩越好， 类别之间的距离平⽅和越⼤越好） ，这样的Calinski-Harabasz分数s会⾼， 分数s⾼则聚类效果越好。
这样的Calinski-Harabasz分数s会⾼， 分数s⾼则聚类效果越好。

使⽤矩阵的迹进⾏求解的理解：矩阵的对⻆线可以表示⼀个物体的相似性
在机器学习⾥， 主要为了获取数据的特征值， 那么就是说， 在任何⼀个矩阵计算出来之后， 都可以简单化， 只要获取矩阵的迹， 就可以表示这⼀块数据的最重要的特征了， 这样就可以把很多⽆关紧要的数据删除掉， 达到简化数据， 提⾼处理速度。
CH需要达到的⽬的：
⽤尽量少的类别聚类尽量多的样本， 同时获得较好的聚类效果。
 

4.3 完整代码

import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import calinski_harabasz_score

# 创建数据集
# X为样本特征， Y为样本簇类别， 共1000个样本， 每个样本2个特征， 共4个簇，
# 簇中⼼在[-1,-1], [0,0],[1,1], [2,2]， 簇⽅差分别为[0.4, 0.2, 0.2, 0.2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[
                  [-1, -1], [0, 0], [1, 1], [2, 2]], cluster_std=[0.4, 0.2, 0.2, 0.2], random_state=9)
#原始数据图
# plt.scatter(X[:, 0], X[:, 1], marker="o")
# plt.show()
#  归为两类
# def KMeans_2():
#     # kmeans训练,且可视化 聚类=2
#     y_pre = KMeans(n_clusters=2, random_state=9).fit_predict(X)
#
#     # 可视化展示
#     plt.scatter(X[:, 0], X[:, 1], c=y_pre)
#     plt.show()
#
#     # 用ch_scole查看最后效果
#     print(calinski_harabasz_score(X, y_pre))
#
# KMeans_2()
# 归为三类
# def KMeans_3():
#     # kmeans训练,且可视化 聚类=3
#     y_pre = KMeans(n_clusters=3, random_state=9).fit_predict(X)
#
#     # 可视化展示
#     plt.scatter(X[:, 0], X[:, 1], c=y_pre)
#     plt.show()
#
#     # 用ch_scole查看最后效果
#     print(calinski_harabasz_score(X, y_pre))
#
# KMeans_3()

# 归为四类
def KMeans_4():
    # kmeans训练,且可视化 聚类=4
    y_pre = KMeans(n_clusters=4, random_state=9).fit_predict(X)

    # 可视化展示
    plt.scatter(X[:, 0], X[:, 1], c=y_pre)
    plt.show()

    # 用ch_scole查看最后效果
    print(calinski_harabasz_score(X, y_pre))

KMeans_4()

4.4 实验结果

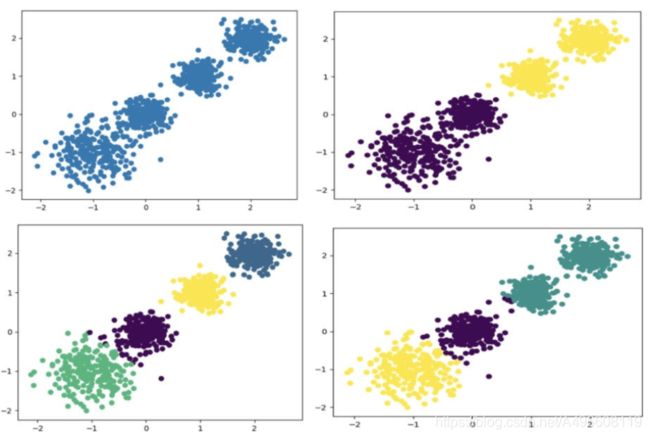
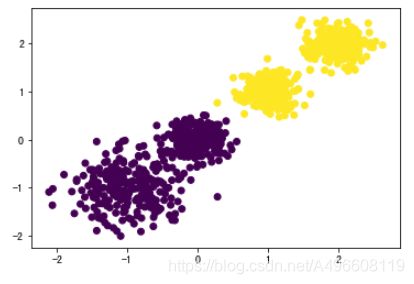
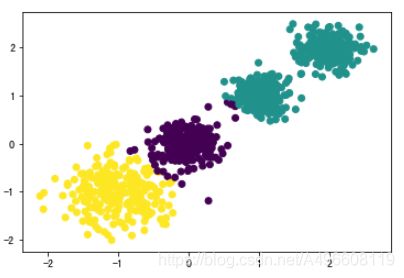
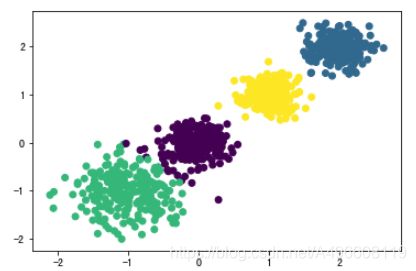
                         原始数据                                                         K=2                                                       K = 3                                                     K = 4

                                                                        CH:3116.1706763322227                             CH:2931.625030199556                           CH: 5924.050613480169

 

 

参考：黑马程序员课程