四元数插值、对偶四元数插值、DQB/DLB
一、四元数与对偶四元数(双四元数)
传送门:四元数,对偶四元数,三维旋转,平移
二、四元数插值
四元数插值 与 向量插值(传送门:[插值算法 - Lerp, NLerp, SLerp])非常类似,
只需要把其中向量换成四元数即可:
L e r p ( q 1 , q 2 ; t ) = ( 1 − t ) q 1 + t q 2 (1) Lerp(\boldsymbol q_1, \boldsymbol q_2; t) = (1-t)\boldsymbol q_1 + t\boldsymbol q_2 \tag 1 Lerp(q1,q2;t)=(1−t)q1+tq2(1)
N L e r p ( q 1 , q 2 ; t ) = ( 1 − t ) q 1 + t q 2 ∥ ( 1 − t ) q 1 + t q 2 ∥ (2) NLerp(\boldsymbol q_1, \boldsymbol q_2; t) = \frac{(1-t)\boldsymbol q_1 + t\boldsymbol q_2}{\Vert(1-t)\boldsymbol q_1 + t\boldsymbol q_2\Vert} \tag 2 NLerp(q1,q2;t)=∥(1−t)q1+tq2∥(1−t)q1+tq2(2)
S L e r p ( q 1 , q 2 ; t ) = sin ( ( 1 − t ) θ ) sin θ q 1 + sin ( t θ ) sin θ q 2 = ( q 2 q 1 ∗ ) t q 1 (3) SLerp(\boldsymbol q_1, \boldsymbol q_2; t) = \frac{\sin((1-t)\theta)}{\sin\theta}\boldsymbol q_1 + \frac{\sin(t\theta)}{\sin\theta}\boldsymbol q_2=(\boldsymbol q_2\boldsymbol q_1^*)^t\boldsymbol q_1 \tag 3 SLerp(q1,q2;t)=sinθsin((1−t)θ)q1+sinθsin(tθ)q2=(q2q1∗)tq1(3)
这里主要说一下 ( 3 ) (3) (3) 式:
式中, θ \theta θ 是 q 1 , q 2 \boldsymbol q_1, \boldsymbol q_2 q1,q2 之间的夹角,定义为: θ = arccos ( q 1 ⋅ q 2 ) \theta = \arccos(\boldsymbol q_1 \cdot \boldsymbol q_2) θ=arccos(q1⋅q2)
不难看出,
在 q 1 \boldsymbol q_1 q1 与 q 2 \boldsymbol q_2 q2 之间插值 ⇔ \Leftrightarrow ⇔ 在 1 1 1 与 q 2 q 1 ∗ \boldsymbol q_2\boldsymbol q_1^* q2q1∗ 之间插值
即 q 2 q 1 ∗ \boldsymbol q_2\boldsymbol q_1^* q2q1∗ 表示了从 q 1 \boldsymbol q_1 q1 到 q 2 \boldsymbol q_2 q2 的变化
显然 q 2 q 1 ∗ \boldsymbol q_2\boldsymbol q_1^* q2q1∗ 是单位四元数,那么 q 2 q 1 ∗ \boldsymbol q_2\boldsymbol q_1^* q2q1∗ 可以表示为:
q 2 q 1 ∗ = cos θ 2 + u sin θ 2 \boldsymbol q_2\boldsymbol q_1^* = \cos \frac{\theta}{2}+\boldsymbol u\sin\frac{\theta}{2} q2q1∗=cos2θ+usin2θ
则
( q 2 q 1 ∗ ) t = cos ( t θ 2 ) + u sin ( t θ 2 ) (\boldsymbol q_2\boldsymbol q_1^*)^t = \cos (\frac{t\theta}{2})+\boldsymbol u\sin(\frac{t\theta}{2}) (q2q1∗)t=cos(2tθ)+usin(2tθ)
可以看出 四元数的 Slerp 是角速度匀速的。
三、对偶四元数插值
3.1 沙勒定理(Chasles Theorem)
沙勒定理是欧拉旋转定理的一个推论。
根据沙勒定理,刚体的最广义位移等价于一个平移加上一个旋转。
因此,刚体运动可分为平移运动与旋转运动。

而这个移动可以合成为 通过绕某根轴的螺旋运动。
3.2 螺旋运动(Screw motion) 与 ScLerp
沙勒定理描述的螺旋运动 (Screw) 如下:
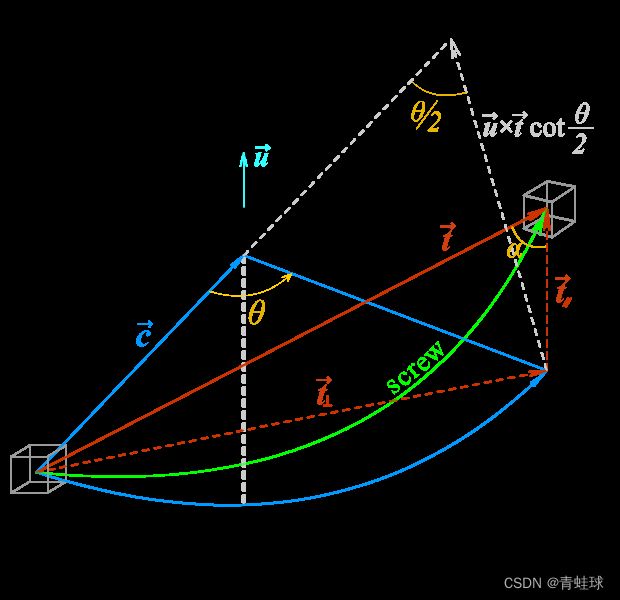
物体经过 O A ⌢ \textcolor{#0088EE}{\overset{\frown}{OA}} OA⌢, A O ′ \textcolor{#BB0000}{AO'} AO′ ⇔ \Leftrightarrow ⇔ 物体直接经过 O O ′ ⌢ \textcolor{#88FF88}{\overset{\frown}{OO'}} OO′⌢
这条浅绿色的螺旋(Screw)路径可以使用对偶四元数来描述 [ 附 B . 1 ] ^{[附B.1]} [附B.1]:
q ^ = cos θ ^ 2 + u ^ sin θ ^ 2 \hat{\boldsymbol q}=\cos\frac{\hat\theta}{2} + \hat{\boldsymbol u}\sin\frac{\hat\theta}{2} q^=cos2θ^+u^sin2θ^
会发现,这个形式和普通的旋转四元数非常相似。
但是此时这里的 θ ^ \hat\theta θ^ 和普通旋转四元数里的 θ \theta θ 已经不是一个意思了。
其中:
{ θ ^ = θ + ε d u ^ = u + ε m = ( 0 + u ⃗ ) + ε ( 0 + m ⃗ ) \left\{ \begin{aligned} \hat\theta&= \textcolor{#CC9900}{\theta} + \varepsilon d \\ \hat{\boldsymbol u} &= \boldsymbol u + \varepsilon \boldsymbol m = (0+\textcolor{#00FFFF}{\vec{\boldsymbol u}}) + \varepsilon(0+\vec{\boldsymbol m}) \end{aligned} \right. {θ^u^=θ+εd=u+εm=(0+u)+ε(0+m)
(其中 d = ∥ t ⃗ ∥ ∥ , d=\Vert\textcolor{#CC0000}{\vec{\boldsymbol t}_\parallel} \Vert, d=∥t∥∥, 矩 m ⃗ = c ⃗ × u ⃗ \vec{\boldsymbol m}= \textcolor{#0088EE}{\vec{\boldsymbol c}} \times \textcolor{#00FFFF}{\vec{\boldsymbol u}} m=c×u)
可以看出,Screw Motion是一个比较理想的插值路径,因此衍生出一种插值方法—— ScLerp (Screw Linear Interpolation),
他的形式与 SLerp 非常相似:
S c L e r p ( q ^ 0 , q ^ 1 ; t ) = ( q ^ 1 q ^ 0 ∗ ) t q ^ 0 ScLerp(\hat{\boldsymbol q}_0, \hat{\boldsymbol q}_1; t) = (\hat{\boldsymbol q}_1\hat{\boldsymbol q}_0^*)^t\hat{\boldsymbol q}_0 ScLerp(q^0,q^1;t)=(q^1q^0∗)tq^0
同样也是角速度匀速的:
( q ^ 1 q ^ 0 ∗ ) t ⟶ t θ ^ ⟶ t θ , t d (\hat{\boldsymbol q}_1\hat{\boldsymbol q}_0^*)^t \longrightarrow t\hat{\theta} \longrightarrow t\theta,td (q^1q^0∗)t⟶tθ^⟶tθ,td
3.3 对偶四元数混合(Dual Quaternion Blending)
在 对偶四元数混合(DQB)中 比较常用的就是 对偶四元数线性混合DLB(Dual Quaternion Linear Blending),
其实它就是 NLerp 的对偶四元数版本:
D L B ( q ^ 1 , q ^ 2 ; t ) = N L e r p ( q ^ 1 , q ^ 2 ; t ) = ( 1 − t ) q ^ 1 + t q ^ 2 ∥ ( 1 − t ) q ^ 1 + t q ^ 2 ∥ (4) DLB(\hat{\boldsymbol q}_1, \hat{\boldsymbol q}_2; t) = NLerp(\hat{\boldsymbol q}_1, \hat{\boldsymbol q}_2; t) = \frac{(1-t)\hat{\boldsymbol q}_1 + t\hat{\boldsymbol q}_2}{\Vert(1-t)\hat{\boldsymbol q}_1 + t\hat{\boldsymbol q}_2\Vert} \tag 4 DLB(q^1,q^2;t)=NLerp(q^1,q^2;t)=∥(1−t)q^1+tq^2∥(1−t)q^1+tq^2(4)
扩展版本:
D L B ( q ^ 1 , … , q ^ n ; w ) = w 1 q ^ 1 + w 2 q ^ 2 + ⋯ + w n q ^ n ∥ w 1 q ^ 1 + w 2 q ^ 2 + ⋯ + w n q ^ n ∥ (5) DLB(\hat{\boldsymbol q}_1, \dots, \hat{\boldsymbol q}_n; \boldsymbol w) = \frac{w_1\hat{\boldsymbol q}_1 + w_2\hat{\boldsymbol q}_2+\dots+ w_n\hat{\boldsymbol q}_n}{\Vert w_1\hat{\boldsymbol q}_1 + w_2\hat{\boldsymbol q}_2+\dots+ w_n\hat{\boldsymbol q}_n \Vert} \tag 5 DLB(q^1,…,q^n;w)=∥w1q^1+w2q^2+⋯+wnq^n∥w1q^1+w2q^2+⋯+wnq^n(5)
3.4 ScLerp 与 DLB 比较
以两个变量为例:
{ D L B ( 1 , q ^ 2 q ^ 1 ∗ ; t ) = ( 1 − t ) + t q ^ 2 q ^ 1 ∗ ∥ ( 1 − t ) + t q ^ 2 q ^ 1 ∗ ∥ S c L e r p ( 1 , q ^ 2 q ^ 1 ∗ ; t ) = ( q ^ 2 q ^ 1 ∗ ) t \left\{ \begin{aligned} DLB(1, \hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*; t) &= \frac{(1-t) + t\hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*}{\Vert(1-t) + t\hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*\Vert} \\ ScLerp(1, \hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*; t) &= (\hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*)^t \end{aligned} \right. ⎩ ⎨ ⎧DLB(1,q^2q^1∗;t)ScLerp(1,q^2q^1∗;t)=∥(1−t)+tq^2q^1∗∥(1−t)+tq^2q^1∗=(q^2q^1∗)t
记 q ^ 2 q ^ 1 ∗ = cos α ^ 2 + n ^ sin α ^ 2 \displaystyle\hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^* = \cos\frac{\hat\alpha}{2} + \hat{\boldsymbol n}\sin\frac{\hat\alpha}{2} q^2q^1∗=cos2α^+n^sin2α^,有
{ D L B ( 1 , q ^ 2 q ^ 1 ∗ ; t ) = ( 1 − t ) + t cos α ^ 2 ∥ ( 1 − t ) + t q ^ 2 q ^ 1 ∗ ∥ + n ^ t sin α ^ 2 ∥ ( 1 − t ) + t q ^ 2 q ^ 1 ∗ ∥ S c L e r p ( 1 , q ^ 2 q ^ 1 ∗ ; t ) = cos t α ^ 2 + n ^ sin t α ^ 2 \left\{ \begin{aligned} DLB(1, \hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*; t) &= \frac{(1-t) + t\cos\frac{\hat\alpha}{2}}{\Vert(1-t) + t\hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*\Vert} +\textcolor{#002288}{\hat{\boldsymbol n}} \frac{t\sin\frac{\hat\alpha}{2}}{\Vert(1-t) + t\hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*\Vert}\\ ScLerp(1, \hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*; t) &= \cos\frac{t\hat\alpha}{2} + \textcolor{#002288}{\hat{\boldsymbol n}}\sin\frac{t\hat\alpha}{2} \end{aligned} \right. ⎩ ⎨ ⎧DLB(1,q^2q^1∗;t)ScLerp(1,q^2q^1∗;t)=∥(1−t)+tq^2q^1∗∥(1−t)+tcos2α^+n^∥(1−t)+tq^2q^1∗∥tsin2α^=cos2tα^+n^sin2tα^
可以看出来, D L B DLB DLB 的转动轴和 S c L e r p ScLerp ScLerp 是同一个(都是 n ^ \textcolor{#002288}{\hat{\boldsymbol n}} n^)
他们的区别只是角度的不同。
与 N L e r p NLerp NLerp 一样, D L B DLB DLB 显然不是角速度匀速的,
记 cos β ^ t 2 = ( 1 − t ) + t cos α ^ 2 ∥ ( 1 − t ) + t q ^ 2 q ^ 1 ∗ ∥ , sin β ^ t 2 = t sin α ^ 2 ∥ ( 1 − t ) + t q ^ 2 q ^ 1 ∗ ∥ \displaystyle\cos\frac{\hat\beta_t}{2} = \frac{(1-t) + t\cos\frac{\hat\alpha}{2}}{\Vert(1-t) + t\hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*\Vert},~~ \sin\frac{\hat\beta_t}{2}=\frac{t\sin\frac{\hat\alpha}{2}}{\Vert(1-t) + t\hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*\Vert} cos2β^t=∥(1−t)+tq^2q^1∗∥(1−t)+tcos2α^, sin2β^t=∥(1−t)+tq^2q^1∗∥tsin2α^,有
{ D L B ( 1 , q ^ 2 q ^ 1 ∗ ; t ) = cos β ^ t 2 + n ^ sin β ^ t 2 S c L e r p ( 1 , q ^ 2 q ^ 1 ∗ ; t ) = cos t α ^ 2 + n ^ sin t α ^ 2 \left\{ \begin{aligned} DLB(1, \hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*; t) &= \cos\frac{\hat\beta_t}{2} + \textcolor{#002288}{\hat{\boldsymbol n}}\sin\frac{\hat\beta_t}{2}\\ ScLerp(1, \hat{\boldsymbol q}_2\hat{\boldsymbol q}_1^*; t) &= \cos\frac{t\hat\alpha}{2} + \textcolor{#002288}{\hat{\boldsymbol n}}\sin\frac{t\hat\alpha}{2} \end{aligned} \right. ⎩ ⎨ ⎧DLB(1,q^2q^1∗;t)ScLerp(1,q^2q^1∗;t)=cos2β^t+n^sin2β^t=cos2tα^+n^sin2tα^
经过实验发现, ∥ β ^ t − t α ^ ∥ \Vert \hat\beta_t - t\hat\alpha \Vert ∥β^t−tα^∥ 很小,可以认为 DLB 路径 近似于 ScLerp 的最短路径效果。
附A 相关公式
A.1
n ⃗ \vec{\boldsymbol n} n为单位向量,那么
n ⃗ × ( n ⃗ × a ⃗ ) = ( n ⃗ T a ⃗ ) n ⃗ − a ⃗ o r n ⃗ × ( a ⃗ × n ⃗ ) = a ⃗ − ( n ⃗ T a ⃗ ) n ⃗ \vec{\boldsymbol n}\times(\vec{\boldsymbol n}\times\vec{\boldsymbol a})=(\vec{\boldsymbol n}^{\mathrm T}\vec{\boldsymbol a})\vec{\boldsymbol n} - \vec{\boldsymbol a} \\ or \\ \vec{\boldsymbol n}\times(\vec{\boldsymbol a}\times\vec{\boldsymbol n})=\vec{\boldsymbol a} - (\vec{\boldsymbol n}^{\mathrm T}\vec{\boldsymbol a})\vec{\boldsymbol n} n×(n×a)=(nTa)n−aorn×(a×n)=a−(nTa)n
附B 推导
B.1 Screw Motion:
图中,向量 c ⃗ \textcolor{#0088EE}{\vec{\boldsymbol c}} c 是垂直于轴 u ⃗ \textcolor{#00FFFF}{\vec{\boldsymbol u}} u 的,
在 O A B \mathrm{OAB} OAB 平面上过点 A \mathrm{A} A 作 O A \mathrm{OA} OA 的垂线,交 O B \mathrm{OB} OB 的延长线与 C \mathrm{C} C
易得:
O A → + A C → = 2 O B → \overrightarrow{\mathrm{OA}} + \overrightarrow{\mathrm{AC}}=2~\overrightarrow{\mathrm{OB}} OA+AC=2 OB
记 x ⃗ = u ⃗ × t ⃗ \vec{\boldsymbol x} = \textcolor{#00FFFF}{\vec{\boldsymbol u}} \times \textcolor{#CC0000}{\vec{\boldsymbol t}} x=u×t,显然 x ⃗ \vec{\boldsymbol x} x 与 A C → \overrightarrow{\mathrm{AC}} AC 方向相同,且 ∥ x ⃗ ∥ = ∥ t ⃗ ⊥ ∥ \Vert\vec{\boldsymbol x}\Vert = \Vert\textcolor{#CC0000}{\vec{\boldsymbol t}_\perp}\Vert ∥x∥=∥t⊥∥,而 ∥ A C → ∥ = ∥ t ⃗ ⊥ ∥ ⋅ cot θ 2 \displaystyle\Vert\overrightarrow{\mathrm{AC}}\Vert = \Vert\textcolor{#CC0000}{\vec{\boldsymbol t}_\perp}\Vert\cdot\cot\frac{\textcolor{#CC9900}{\theta}}{2} ∥AC∥=∥t⊥∥⋅cot2θ,所以
A C → = u ⃗ × t ⃗ ⋅ cot θ 2 O A → = u ⃗ × ( t ⃗ × u ⃗ ) = t ⃗ − ( u ⃗ T t ⃗ ) u ⃗ \overrightarrow{\mathrm{AC}}=\textcolor{#00FFFF}{\vec{\boldsymbol u}} \times \textcolor{#CC0000}{\vec{\boldsymbol t}} \cdot\cot\frac{\textcolor{#CC9900}{\theta}}{2} \\ \overrightarrow{\mathrm{OA}} = \textcolor{#00FFFF}{\vec{\boldsymbol u}} \times ( \textcolor{#CC0000}{\vec{\boldsymbol t}} \times \textcolor{#00FFFF}{\vec{\boldsymbol u}}) = \textcolor{#CC0000}{\vec{\boldsymbol t}} - ( \textcolor{#00FFFF}{\vec{\boldsymbol u}}^{\mathrm T} \textcolor{#CC0000}{\vec{\boldsymbol t}} ) \textcolor{#00FFFF}{\vec{\boldsymbol u}} AC=u×t⋅cot2θOA=u×(t×u)=t−(uTt)u
所以
t ⃗ − ( u ⃗ T t ⃗ ) u ⃗ + u ⃗ × t ⃗ ⋅ cot θ 2 = 2 c ⃗ \textcolor{#CC0000}{\vec{\boldsymbol t}} - ( \textcolor{#00FFFF}{\vec{\boldsymbol u}}^{\mathrm T} \textcolor{#CC0000}{\vec{\boldsymbol t}} ) \textcolor{#00FFFF}{\vec{\boldsymbol u}} + \textcolor{#00FFFF}{\vec{\boldsymbol u}} \times \textcolor{#CC0000}{\vec{\boldsymbol t}} \cdot\cot\frac{\textcolor{#CC9900}{\theta}}{2} = 2 \textcolor{#0088EE}{\vec{\boldsymbol c}} t−(uTt)u+u×t⋅cot2θ=2c
那么轴的矩 m ⃗ \vec{\boldsymbol m} m 即为:
m ⃗ = c ⃗ × u ⃗ = 1 2 ( t ⃗ × u ⃗ + u ⃗ × t ⃗ × u ⃗ ⋅ cot θ 2 ) = 1 2 ( t ⃗ × u ⃗ + ( t ⃗ − ( u ⃗ T t ⃗ ) u ⃗ ) ⋅ cot θ 2 ) \begin{aligned} \vec{\boldsymbol m} &= \textcolor{#0088EE}{\vec{\boldsymbol c}} \times \textcolor{#00FFFF}{\vec{\boldsymbol u}} \\ &= \frac{1}{2}\big( \textcolor{#CC0000}{\vec{\boldsymbol t}} \times \textcolor{#00FFFF}{\vec{\boldsymbol u}} + \textcolor{#00FFFF}{\vec{\boldsymbol u}} \times \textcolor{#CC0000}{\vec{\boldsymbol t}} \times \textcolor{#00FFFF}{\vec{\boldsymbol u}} \cdot\cot\frac{\textcolor{#CC9900}{\theta}}{2}\big) \\ &= \frac{1}{2}\Bigg( \textcolor{#CC0000}{\vec{\boldsymbol t}} \times \textcolor{#00FFFF}{\vec{\boldsymbol u}} + \Big(\textcolor{#CC0000}{\vec{\boldsymbol t}} - ( \textcolor{#00FFFF}{\vec{\boldsymbol u}}^{\mathrm T} \textcolor{#CC0000}{\vec{\boldsymbol t}} ) \textcolor{#00FFFF}{\vec{\boldsymbol u}}\Big)\cdot\cot\frac{\textcolor{#CC9900}{\theta}}{2}\Bigg) \end{aligned} m=c×u=21(t×u+u×t×u⋅cot2θ)=21(t×u+(t−(uTt)u)⋅cot2θ)
记四元数 q = q 0 + q ⃗ = cos θ 2 + u ⃗ sin θ 2 \displaystyle\boldsymbol q = q_0 + \vec{\boldsymbol q} = \cos\frac{\textcolor{#CC9900}{\theta}}{2} + \textcolor{#00FFFF}{\vec{\boldsymbol u}}\sin\frac{\textcolor{#CC9900}{\theta}}{2} q=q0+q=cos2θ+usin2θ,则有:
sin θ 2 m ⃗ = 1 2 ( t ⃗ × q ⃗ + ( t ⃗ − ( u ⃗ T t ⃗ ) u ⃗ ) ⋅ cos θ 2 ) \sin\frac{\textcolor{#CC9900}{\theta}}{2}\vec{\boldsymbol m} = \frac{1}{2}\Bigg( \textcolor{#CC0000}{\vec{\boldsymbol t}} \times \vec{\boldsymbol q} + \Big(\textcolor{#CC0000}{\vec{\boldsymbol t}} - ( \textcolor{#00FFFF}{\vec{\boldsymbol u}}^{\mathrm T} \textcolor{#CC0000}{\vec{\boldsymbol t}} ) \textcolor{#00FFFF}{\vec{\boldsymbol u}}\Big)\cdot\cos\frac{\textcolor{#CC9900}{\theta}}{2}\Bigg) sin2θm=21(t×q+(t−(uTt)u)⋅cos2θ)
我们知道, u ⃗ T t ⃗ = ∥ t ⃗ ∥ ∥ \textcolor{#00FFFF}{\vec{\boldsymbol u}}^{\mathrm T} \textcolor{#CC0000}{\vec{\boldsymbol t}}=\Vert\textcolor{#CC0000}{\vec{\boldsymbol t}_\parallel} \Vert uTt=∥t∥∥,记它为 d d d,则有:
sin θ 2 m ⃗ + d 2 u ⃗ cos θ 2 = 1 2 ( t ⃗ × q ⃗ + q 0 t ⃗ ) (1) \sin\frac{\textcolor{#CC9900}{\theta}}{2}\vec{\boldsymbol m} + \frac{d}{2}\textcolor{#00FFFF}{\vec{\boldsymbol u}}\cos\frac{\textcolor{#CC9900}{\theta}}{2}=\frac{1}{2} ( \textcolor{#CC0000}{\vec{\boldsymbol t}} \times \vec{\boldsymbol q}+q_0\textcolor{#CC0000}{\vec{\boldsymbol t}}) \tag{1} sin2θm+2ducos2θ=21(t×q+q0t)(1)
由于:
q ^ = q + ε q ′ = q + ε 2 t q = q 0 + q ⃗ + ε 2 ( − t ⃗ T q ⃗ + q 0 t ⃗ + t ⃗ × q ⃗ ) = q 0 − ε 1 2 t ⃗ T q ⃗ + q ⃗ + ε 1 2 ( q 0 t ⃗ + t ⃗ × q ⃗ ) \begin{aligned} \hat{\boldsymbol q} &=\boldsymbol q+\varepsilon\boldsymbol q'=\boldsymbol q+\frac{\varepsilon}{2}\boldsymbol t\boldsymbol q \\ &= q_0 + \vec{\boldsymbol q} + \frac{\varepsilon}{2}(-\textcolor{#CC0000}{\vec{\boldsymbol t}}^{\mathrm T}\vec{\boldsymbol q}+q_0 \textcolor{#CC0000}{\vec{\boldsymbol t}}+ \textcolor{#CC0000}{\vec{\boldsymbol t}}\times\vec{\boldsymbol q}) \\ &=q_0-\varepsilon\frac{1}{2} \textcolor{#CC0000}{\vec{\boldsymbol t}} ^{\mathrm T}\vec{\boldsymbol q}~~~+~~~\vec{\boldsymbol q}+\varepsilon\frac{1}{2}(q_0 \textcolor{#CC0000}{\vec{\boldsymbol t}} + \textcolor{#CC0000}{\vec{\boldsymbol t}}\times\vec{\boldsymbol q}) \end{aligned} q^=q+εq′=q+2εtq=q0+q+2ε(−tTq+q0t+t×q)=q0−ε21tTq + q+ε21(q0t+t×q)
由于 t ⃗ T q ⃗ = t ⃗ T u ⃗ sin θ 2 = d sin θ 2 \displaystyle \textcolor{#CC0000}{\vec{\boldsymbol t}}^{\mathrm T}\vec{\boldsymbol q}= \textcolor{#CC0000}{\vec{\boldsymbol t}}^{\mathrm T}\textcolor{#00FFFF}{\vec{\boldsymbol u}}\sin\frac{\textcolor{#CC9900}{\theta}}{2}=d\sin\frac{\textcolor{#CC9900}{\theta}}{2} tTq=tTusin2θ=dsin2θ,并带入(1)式得:
q ^ = ( cos θ 2 − ε d 2 sin θ 2 ) + ( ( sin θ 2 + ε d 2 cos θ 2 ) u ⃗ + ε sin θ 2 m ⃗ ) = ( cos θ 2 − ε d 2 sin θ 2 ) + ( ( sin θ 2 + ε d 2 cos θ 2 ) u ⃗ + ε sin θ 2 m ⃗ + ε d 2 cos θ 2 ε m ⃗ ) = ( cos θ 2 − ε d 2 sin θ 2 ) + ( sin θ 2 + ε d 2 cos θ 2 ) ( u ⃗ + ε m ⃗ ) \begin{aligned} \hat{\boldsymbol q} &= \Big(\cos\frac{\textcolor{#CC9900}{\theta}}{2} - \varepsilon\frac{d}{2}\sin\frac{\textcolor{#CC9900}{\theta}}{2}\Big)+\Big( (\sin\frac{\textcolor{#CC9900}{\theta}}{2}+\varepsilon\frac{d}{2}\cos\frac{\textcolor{#CC9900}{\theta}}{2})\textcolor{#00FFFF}{\vec{\boldsymbol u}}+\varepsilon\sin\frac{\textcolor{#CC9900}{\theta}}{2}\vec{\boldsymbol m} \Big) \\ &= \Big(\cos\frac{\textcolor{#CC9900}{\theta}}{2} - \varepsilon\frac{d}{2}\sin\frac{\textcolor{#CC9900}{\theta}}{2}\Big)+\Big( (\sin\frac{\textcolor{#CC9900}{\theta}}{2}+\varepsilon\frac{d}{2}\cos\frac{\textcolor{#CC9900}{\theta}}{2})\textcolor{#00FFFF}{\vec{\boldsymbol u}}+\varepsilon\sin\frac{\textcolor{#CC9900}{\theta}}{2}\vec{\boldsymbol m} + \textcolor{#FF0000}{\varepsilon\frac{d}{2}\cos\frac{\theta}{2}\varepsilon\vec{\boldsymbol m}}\Big) \\ &= \Big(\cos\frac{\textcolor{#CC9900}{\theta}}{2} - \varepsilon\frac{d}{2}\sin\frac{\textcolor{#CC9900}{\theta}}{2}\Big)+\Big( \sin\frac{\textcolor{#CC9900}{\theta}}{2}+\varepsilon\frac{d}{2}\cos\frac{\textcolor{#CC9900}{\theta}}{2}\Big)\Big(\textcolor{#00FFFF}{\vec{\boldsymbol u}}+\varepsilon\vec{\boldsymbol m}\Big) \end{aligned} q^=(cos2θ−ε2dsin2θ)+((sin2θ+ε2dcos2θ)u+εsin2θm)=(cos2θ−ε2dsin2θ)+((sin2θ+ε2dcos2θ)u+εsin2θm+ε2dcos2θεm)=(cos2θ−ε2dsin2θ)+(sin2θ+ε2dcos2θ)(u+εm)
由泰勒展开式知:
{ cos ( θ + ε d 2 ) = cos θ 2 − ε d 2 sin θ 2 sin ( θ + ε d 2 ) = sin θ 2 + ε d 2 cos θ 2 \left\{ \begin{aligned} \cos\Big(\frac{\theta+\varepsilon d}{2}\Big) &= \cos\frac{\theta}{2} - \varepsilon\frac{d}{2}\sin\frac{\theta}{2} \\ \sin\Big(\frac{\theta+\varepsilon d}{2}\Big) &= \sin\frac{\theta}{2} + \varepsilon\frac{d}{2}\cos\frac{\theta}{2} \end{aligned} \right. ⎩ ⎨ ⎧cos(2θ+εd)sin(2θ+εd)=cos2θ−ε2dsin2θ=sin2θ+ε2dcos2θ
则上式则可以写为:
q ^ = cos ( θ + ε d 2 ) + ( u ⃗ + ε m ⃗ ) sin ( θ + ε d 2 ) = cos θ ^ 2 + u ^ sin θ ^ 2 \begin{aligned} \hat{\boldsymbol q} &= \cos\Big(\frac{\theta+\varepsilon d}{2}\Big) + \Big(\vec{\boldsymbol u}+\varepsilon\vec{\boldsymbol m}\Big)\sin\Big(\frac{\theta+\varepsilon d}{2}\Big) \\ &= \cos\frac{\hat\theta}{2} + \hat{\boldsymbol u}\sin\frac{\hat\theta}{2} \end{aligned} q^=cos(2θ+εd)+(u+εm)sin(2θ+εd)=cos2θ^+u^sin2θ^
参考
四元数插值与均值(姿态平滑) https://www.cnblogs.com/21207-iHome/p/6952004.html
Skinning with Dual Quaternions
Geometric Skinning with Approximate Dual Quaternion Blending
Hand-eye calibration using dual quaternions