FMS中基于神经网络的多agv系统多状态调度算法
原文
A neural network based multi-state scheduling algorithm for multi-AGV system in FMS
发表于Journal of Manufacturing Systems,二区,机翻,最好配合原文食用
abstract
柔性制造系统(FMS)由于其在灵活性、可维护性和建造成本方面的众多优势,在过去几年里受到了越来越多的关注。AGV运输系统的应用提高了FMS的灵活性,同时也对AGV调度算法提出了更高的要求。本文提出了一种新的AGV多状态调度算法(MSSA),该算法在AGV利用率和FMS总加工时间之间进行了很好的权衡。与经典的空闲调度策略相比,MSSA在每次计算中调度更多agv和任务,使其优化目标更接近全局优化目标。利用神经网络对行程时间进行预测,提高了算法的时间精度。采用5个因素作为神经网络输入,分别表达车辆状态、行驶距离、AGV轨迹和AGV多次碰撞对行驶时间的影响。仿真实验表明,该算法在处理总时间跨度、AGV负荷率、AGV利用率和任务执行时间等方面具有优势。该算法已在实际空调生产线上得到了应用。
2. 问题建模
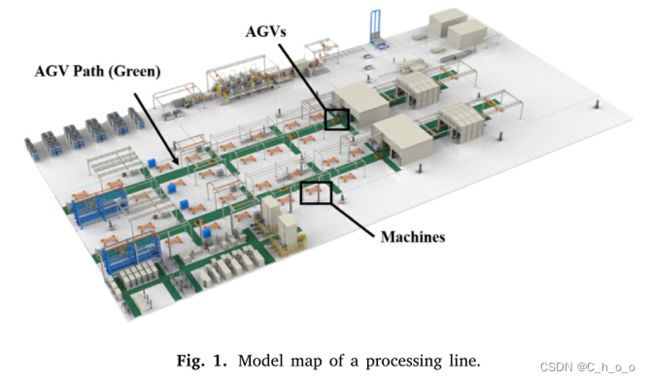
图1为所研究的FMS模型图。该系统由数控加工机床和多台agv运输系统组成。在信息系统的管理下,该FMS可以加工多种类型的产品。FMS的目标是尽快处理尽可能多的产品。为了实现这一目标,加工线上的每台机器都将被最大限度地利用,这意味着机器的闲置时间必须最小化。因此,对于物料搬运系统来说,目标是将半成品尽快运到机器上。AGV作为一种主要的交通工具,广泛应用于许多自动化的FMSs中。设计一个有效的调度AGV算法关系到整个FMS的效率。在本节中,我们首先提供了所研究的FMS的详细描述,随后建立了自动FMS中AGV调度问题的数学模型。
2.1. 所研究的FMS的布局
本文研究的FMS包括两条生产线,每条生产线有19台机器。在这个FMS中,总共有38台加工机。模型图的详细布局如图2所示。在这个FMS中,两条加工线被中路分隔成上下两部分。
这个FMS是一个流水车间,原料需要每台机器加工一次。这些机器一次只能加工一件半成品。因此,为了得到一件产品,一种原料需要经过19道加工工序(一台机器一道工序)。生成运输任务,将半成品从前一台机器运输到下一台机器,这两者都在同一加工线上。
2.2. 数学模型
表示法见表1。
FMS的最终目标是用最少的时间处理产品。由于原材料要经过每台机器的机械加工才能成为产品,最后一台机器获得的半成品就是最终产品。本文主要研究AGV调度问题,而不是作业调度问题和工人调度问题。因此,假设如下。
假设1:每台机器加工半成品的时间是固定的。每个产品的加工顺序是固定的,相同的。
根据假设1,为了使整条加工线的总制造跨度最小,完成所有运输任务的时间应尽可能小。该优化目标如式(1)所示。
根据实际生产情况,提出以下假设:
假设2:AGV在运输产品时等待会导致能源浪费和安全隐患,需要避免。因此,在目标机器没有产品之前,运输任务不能启动。
假设3:每辆AGV装载和卸载的时间是固定的,是相同的。
计算模型的优化目标如式(1),则模型的约束条件为:
其中,X(Ri,Tj)为决策变量,决定是否将运输任务Tj分配给AGV Ri。

 表示AGV Ri在负载或空载状态为c时从Pm点到Pn点的时间。
表示AGV Ri在负载或空载状态为c时从Pm点到Pn点的时间。
c为AGV的装载状态。当为1时,表示AGV载着货物行驶。当AGV无货行驶时,则为0。
![]() 分别为AGV装载和卸载所需的时间。
分别为AGV装载和卸载所需的时间。
式(2)计算任务Tj的完成时间。式(3)计算AGV在任务上的执行时间。式(5)表示,该运输任务的开始时间为该运输任务生成时间与AGV执行上一运输任务完成时间的较大值。式(6)保证每个任务只能被分派到一个AGV上。式(7)保证运输任务必须等待,直到目标机器上没有产品。
3.AGV任务的多状态调度算法
3.1. MSSA的优化目标
因为式(1)中提出的优化目标是一个时间扩展值,不能瞬时计算。一次计算,式(1)可转化为式(8)。
其中,TC表示在计算中分派的传输任务集。
但是,由于整个生产过程中有多次计算,Eq.(8)的优化函数可能会导致下一次计算结果较差。因此,大多数学者以任务执行总时间为优化目标,计算公式为式(9)。
图3显示了这两个优化目标的差异。在这个甘特图中有两个计算。在第一次计算中,需要调度三个任务(T1、T2、T3),在第二次计算中调度另外三个任务(T4、T5、T6)。
在第一次计算中,式(8)的优化目标得到的结果优于式(9)(t1和t2)。但是,由于总任务执行时间较长,导致第二次计算(t3和t4)的性能较差。
根据假设3,式(3)中的tL和tU为定值。 表示AGV从拾取点到运输任务目标点所花费的时间,由AGV的性能和运输任务的行驶距离决定。因此,可将式(9)转化为式(10)
表示AGV从拾取点到运输任务目标点所花费的时间,由AGV的性能和运输任务的行驶距离决定。因此,可将式(9)转化为式(10)
预定的等待时间定义如下。
定义1(预定轮候时间):运输任务Tj的预定等待时间是指AGV从分配运输任务到AGV到达任务拾取点的时间,可由式(11)计算。
本文提出的算法将每次计算中调度的所有任务的预定等待时间作为优化目标。但是,每次计算所涉及的运输任务的数量会影响最终的优化结果。这个效应将在定理1和定理2中讨论。
在给出定理之前,必须给出如下的定义。
定义2(优化函数):设函数f(xj), Tj∈T为优化函数,通过合理调度agv,可得到xj的最小值。该函数中的xj为优化目标,可为WTj或ETj。由于调度结果会相互影响,未建立函数f(xj)的加法交换律,如式(12)所示。添加的顺序表示任务的调度顺序。
![]()
根据上述优化函数的定义,可以提出定理1。
定理1:函数f(xj)满足以下不等式。
证明见原文
根据定理1,得到定理2。设ESW为解的总任务执行时间,根据式(10)的优化目标得到。设EMIN为任务执行总时间的最小值。δ表示这两个值的差。
定理2:不等式式(16)必须满足。
![]()
δ随着每次计算分配给agv的任务数量的增加而减少.
证明见原文
根据定理2,以每次计算中调度任务的预定等待时间为优化目标的算法,可以在一定程度上获得所有任务完成时间的最优解。但结果取决于每次计算所涉及的任务数量。基于这一特性,MSSA的输入将如3.2节设计。
3.2. MSSA的输入
AGV调度算法通常有两个输入:待调度任务和AGV。根据定理2,每次计算中分配的任务应该尽可能多。一般情况下,AGV调度算法在AGV空闲时调度任务,即空闲调度策略。在解决AGV任务调度问题时,通常将空闲调度策略与其他模型相结合[13,14]。然而,由于每个任务的执行时间不同,大多数情况下只有少数agv是空闲的,这意味着每次计算只会调度少数任务。
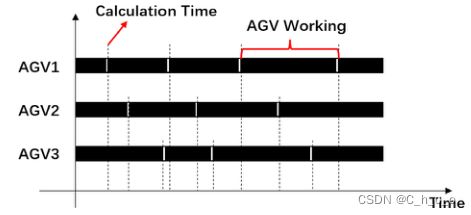
这种现象可以用图5中的甘特图来说明。在本例中,为各种任务分配了三辆agv。由于每个任务的出行时间和运行时间的不确定性,每个任务所花费的时间是不同的。在本例中,每次计算中只有一个AGV参与,这意味着每次计算只向AGV分派一个运输任务。根据定理2,每次计算分配给agv的任务越多,得到的结果越好。为了增加每次计算涉及的agv数量,每次计算都会涉及多状态agv
根据agv执行任务的操作情况,可以将agv分为五种状态,用四维向量ST来描述。这五个状态是:
1. 空闲状态,即AGV正在等待任务,用ST0 =[0,0,0,0]表示。
2. 空移动状态,即AGV正在接近任务的拾取点,用ST1 =[1,1,1,1]表示。
3. 装载状态,即AGV在任务的拣货点装载货物,用ST2 =[0,1,1,1]表示。
4. 全移动状态,即AGV正在将货物运送到任务的目标点,用ST3 =[0,0,1,1]表示。
5. 卸货状态,即AGV正在任务目标点卸货,用ST5 =[0,0,0,1]表示。
具有上述状态的AGV集合就是MSSA的AGV输入。MSSA的任务输入是计算时生成的所有运输任务的集合。因为计算的AGV输入从空闲AGV集合扩展到所有状态AGV集合。计算预定等待时间的公式(式(11))改为式(25)。
其中,![]() 表示AGV Ri的逻辑点,由式(26)定义。
表示AGV Ri的逻辑点,由式(26)定义。![]() 为AGV Ri当前正在执行的任务的操作时间向量,由4个元素组成,由式(27)计算
为AGV Ri当前正在执行的任务的操作时间向量,由4个元素组成,由式(27)计算
其中![]() 表示AGV Ri执行的运输任务。
表示AGV Ri执行的运输任务。
式(27)中,第一个元素和第三个元素是AGV的旅行时间,直到任务完成后才能得到。所以在MSSA中使用预测值。因此,预测值的准确性将直接影响MSSA的性能,这将在第4节讨论。
3.3. 遗传算法
3.1节定义了优化函数,通过调度合理的agv为任务寻找最优优化目标。因此,优化函数的性能会影响MSSA的结果。为了得到全局最优解,我们采用遗传算法作为优化函数。遗传算法是一种经典的启发式算法,由许多学者在AGV调度领域开发[20-23]。Chaudhari和Thakkar比较了各种智能算法的性能,结果表明遗传算法在调度问题[24]上具有良好的性能。本文将遗传算法与空转调度策略和多目标优化算法相结合。染色体编码如图6所示。块的索引表示任务索引,每个块中的编号表示分配到该任务的AGV。
适应度函数为式(10)中提出的优化目标。通过上述染色体和适应度函数的设计,将整个过程设计为算法1。
4. 基于神经网络的旅行时间预测
在3.2节中,优化目标是根据出行时间计算的,可以提供一个预测值。预测的准确性将直接影响算法的性能。一般来说,可以用距离与速度的比值粗略估计旅行时间。然而,影响旅行时间的因素远不止距离和速度。本文在预测旅行时间时,需要考虑5个因素,如表2所示。
CTD反映了出行距离对出行时间的影响。由于AGV会以相对较低的速度通过弯道,因此引入CTN来反映转弯对行驶时间的影响。CLS表示AGV的加载状态,当AGV加载时,速度较低。除了上述因素外,还引入了CPCS和CPCD来评估两辆agv之间的冲突。
在多机器人系统中,死锁和避碰是不可避免的,这会影响运动时间。本文在预测出行时间时考虑了两类冲突,如图7所示。图7(A)为同一方向的冲突,即两车路径重叠部分在同一方向。在这种情况下,两个agv会相互影响,但不存在死锁。
因此,只会比平时稍长一点。但是,在图7(B)的情况下,必须有一辆AGV在等待另一辆AGV,这可能会导致等待时间过长。CPCS和CPCD用来反映这两种情况,这是通过相加所有冲突边的长度计算出来的。例如,图7(A)中,CPCS=6,CPCD=0。图7(B)中,CPCS=0,CPCD=6。
4.1. 神经网络训练
这五个因素是神经网络的输入,网络的输出是预测的旅行时间。采用了一个十神经元隐层和一个输出层的神经网络。神经网络的结构如图8所示。
5. 实验
5.1. 神经网络训练
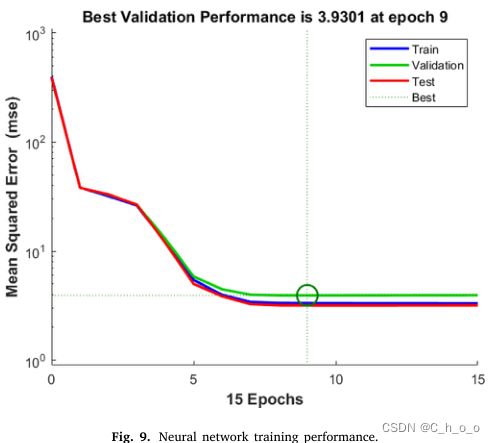
在Matlab上建立了神经网络。训练算法为Levenberg-Marquardt算法(LMA)。从仿真中采集了20 000个样本,其中14 000个样本用于训练神经网络,3000个样本用于验证,3000个样本用于测试。损失函数采用均方误差(MSE)。训练效果如图9所示
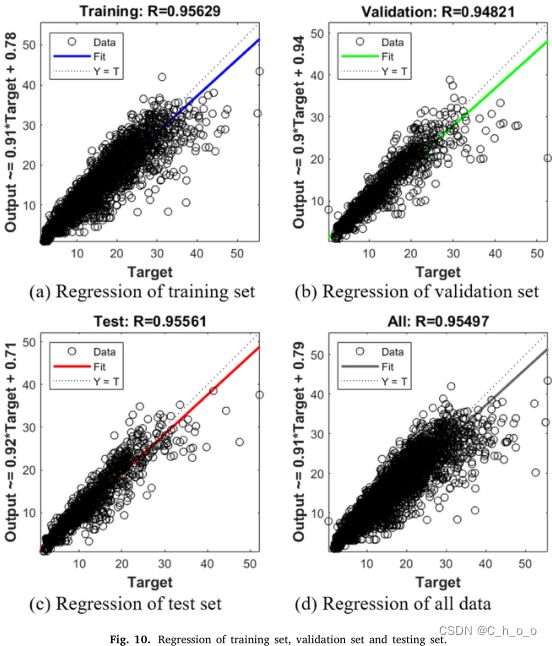
训练集、验证集和测试集的回归图如图10所示。
5.2. 实验指标
在FMS中,运输货物所花费的时间、agv的利用率和加工产品的时间跨度是三个最重要的指标。运输货物所花费的时间反映了调度算法的合理性。agv的利用率决定了执行所有运输任务需要多少agv。一个产品的加工时间是最终的优化目标。在本文中,所有用于测试算法性能的评价指标都会集中在这三个方面,如表3所示。
5.3. 仿真设置
仿真实验在Intel (R) Xeon(R) Platinum 8280L CPU的计算机上进行。并用Java编写了仿真程序。神经网络在Matlab R2021a上进行训练,封装成jar包,由Java程序调用。agv的路径规划采用A*算法。
实验中测试了三种算法,分别是MSSA、GA和带有神经网络预测的MSSA (msa - nnp)。经典遗传算法与空闲调度策略相结合,即每次计算只调度空闲的agv。本文还提出了另外两种算法。对于无神经网络行程时间预测的MSSA,行程时间预测与速度距离的关系。
所有的实验都是从所有机器的完整状态开始的,这意味着当实验开始时,每台机器都有一个半成品。GA的种群大小设为100,突变率设为0.07。AGV参数如表4所示,根据实际生产场景推导。每组实验进行3次,取各指标的平均值。
5.4. 实验A:不同AGV数量
在这组实验中,每台机器的处理时间设置为12分钟。AGV编号的取值范围为2 ~ 6。实验数值结果如表5所示。
根据结果绘制了一些图,以更直观地显示算法的性能,如图11所示。
随着AGV数量的增加,GA在负载率、行驶距离和执行时间上的性能都有所下降。由于GA采用了空闲调度策略,当agv处于空闲状态时,GA更倾向于将任务分配给空闲的agv。然而,空闲的AGV不一定是完成这项任务的最佳AGV,这可以从图12中解释。
在本例中,AGV 1将货物运输到机器A。AGV 2和AGV 3正在等待任务。这时,机器B完成了它的处理并生成了一个从机器B到机器C的传输任务。对于空转调度策略,该运输任务将分配给AGV 2或AGV 3。然而,AGV 1完成当前任务并到达机器B⃝所花的时间将小于空闲AGV到达机器B所花的时间。任务一旦被分配到空闲的agv上,完成任务的时间就会增加,因此会产生较高的利用率,如图11(B)所示。而对于MSSA,可以通过比较每辆AGV所花费的时间来做出最优决策,而不是只考虑空闲的AGV。正是因为这种比较是基于时间预测的,如果预测的时间不准确,任务执行的时间就会变长,导致总make-span变长。这就是为什么MSSA可以像msa - nnp一样在其他指标上保持良好的性能,但在总生产周期上表现不佳。
5.5. 实验B:不同的处理时间
...
5.6. 实验分析
...
6. 结论
本文研究了FMS中对调度精度要求较高的AGV任务调度问题。针对经典的空载调度策略存在的短视问题,提出了一种多agv运输系统的多状态调度算法。建立了一个隐含层和输出层的神经网络来预测AGV的行程时间,并将该神经网络集成到MSSA中以提高其预测精度。与经典的GA怠速调度策略相比,该算法(msa - nnp)在AGV利用率、任务运输距离和总最大完成时间等方面具有优势。将该算法应用于实际空调厂,如图16所示。在这个工厂,5辆agv用于运输加工线上的半成品。MSSA的应用提高了AGV效率,减小了总行程。
在未来的研究中,我们将从以下两个方面继续改进所提出的算法。第一个重点是提出一个任务链模型,通过每次计算涉及更多的任务来进一步提升MSSA的性能,这意味着优化目标更接近式(1)的最终优化目标。另一个重点是通过使用其他机器学习模型或采用更多的因子作为输入来提高出行时间预测函数的精度。