【多传感器融合定位1】惯导模型、内参标定、allan方差
从今天开始,更一个系列,主要是记录这段时间用多传感器做组合定位的学习过程,其中包括惯导、GPS、轮速、lidar等传感器进行定位的方法,以及利用惯导做组合定位的方法,希望大家一起交流。如有问题,请大佬指正。
接下里是第一篇,惯导相关内容。
目录
1.惯导简介
(1)原理
机械陀螺
激光陀螺&光纤陀螺
MEMS陀螺
加速度计
(2)误差组成
随机误差
常值误差
误差模型
2. 标定
(1)allan方差
(2)内参标定
内参模型
3. 仿真及标定程序
(1)利用psins工具箱产生惯导数据
(2)添加噪声数据
(3)标定allan方差
(4)gnss-ins-sim仿真
(5)利用imu_tk仿真
1.惯导简介
(1)原理
以下部分摘录深蓝课程:
机械陀螺
- 机械陀螺具有定轴性和进动性
- 定轴性:高速运动的陀螺,陀螺的自传轴在惯性空间中指向保持稳定不变,指向固定的方向,同时反抗任何改变转轴的力量。
- 进动性:当转子高速旋转时,若外力矩作用于外环轴,陀螺仪将绕内环轴转动;若外力矩作用于内环轴,陀螺仪将绕外环轴转动。其转动角速度方向与外力矩作用方向互相垂直。
激光陀螺&光纤陀螺
利用光的干涉效应,从棱镜中发射的两束光,如果陀螺相对于惯性空间没有运动,那么两光光程相等,如果有角速度,光程不相等时,会产生干涉。
光纤陀螺和激光陀螺同样利用sagnac效应,但是是利用光纤传输光信号。
MEMS陀螺
科里奥利力(Coriolis force,简称为科氏力),是对旋转体系(比如自传的地球,旋转的圆盘等)中进行直线运动的质点由于惯性相对于旋转体系产生的直线运动的偏移的一种描述。MEMS中的器件会做直线运动,当载体存在旋转时,会产生科氏力,从而可以计算角速度。
加速度计
当运载体相对惯性空间做加速度运动时,仪表壳体也随之做相对运动,质量块保持惯性,朝着与加速度方向相反的方向产生位移(拉伸或压缩弹簧)。当位移量达到一定值时,弹簧给出的力使质量块以同一加速度相对惯性空间做加速运动,加速度的大小与方向影响质量块相对位移的方向及拉伸量。
(2)误差组成
imu的误差分为随机误差和常值误差,随机误差具有随机性,常值误差常称为内参的误差,其包括常值bias和安装误差。
随机误差
分为陀螺议的随机误差和加速度计的随机误差,以下分别介绍:
- 量化噪声
- 量化产生的噪声,数字传感器都会存在的噪声。由于AD采集是将连续的信号转换成离散的信号,所以存在误差,当采集的步长越长,量化噪声越大。
- 角度随机游走
- 速度随机游走
- 加速度计相关的随机游走误差
- 单位为m/s/√h 或者ug/√hz,g=9.8m/s^2
- 是加速度积分得到速度的过程中的一阶马尔可夫过程,也就是速度随机游走
- 角速率随机游走
- 由于角加速度具有白噪声误差,积分后也会变成一阶马尔可夫过程,形成角速度随机游走。
- 加速度随机游走
- 加速度计输出测量加速度的随机游走误差
- 零偏不稳定性
- Bias,不是一个固定参数,在一个范围内随机漂移。其随时间变化缓慢,利用一个该来区间描述它落在这个区间的可能性,时间越长区间越大。
- 陀螺议单位为deg/h,deg/s。加速度及单位为ug
- 计算陀螺零偏不稳定性的方法是采集一段数据,去除趋势项,再计算均方差。那么显然采样时间越长,意味着平滑的数据长度长,得到的零偏稳定性数值也就越好。 因此在评估精度时,采样时间也是要考量的参数之一。
- 如果两个陀螺,指标相同,但是采样时间不同,采样时间越小的陀螺,稳定性越好
- 速率斜坡
- 误差的趋势,趋势性误差
- 随机误差,是指你无法用确定性模型去拟合并消除它,最多只能用概率模型去描述它,这样得到的预测结果也是概率性质的。
- 趋势性误差,是可以直接拟合消除的,在陀螺里产生这种误差最常见的原因是温度引起零位变化,可以通过温补来消除
- 零偏重复性
- 多次启动时,零偏不相等,因此会有一个重复性误差。在实际使用中,需要每次上电都重新估计一次。
常值误差
1. 常值bias,常称作零偏
2. 刻度系数误差
3.安装误差
误差模型
2. 标定
(1)allan方差
原理不过多展开,allan方差标定的是随机误差,标定一个数值大概知道陀螺的性能,给后续卡尔曼滤波作为一个参考,说大概,是因为卡尔曼滤波参数是需要根据经验值调教的。所以不用太拘泥与精确获取。组合导航的Kalman滤波噪声参数设置,主要有用的是角度随机游走系数(用于设置Q阵)和零偏不稳定性系数(用于设置一阶马氏过程的方差)。
以下直接摘抄知乎大佬的计算公式:
其实allan方差计算并不复杂,下面的例子只针对陀螺,把陀螺建模为:
其中我们只关心:
- N: angle random walk(-1/2斜率)
- K: rate random walk(1/2斜率)
- B: bias instability(0斜率)
(2)内参标定
利用imutk的思路进行内参标定,根据误差模型,可以得到理想输出和真实输出的误差,根据这个误差构建优化方程,进行优化求解,得到所求内参。imutk流程图:
内参模型
为简化求解,假设加速度计的安装坐标系的x轴与imu坐标系的的x轴一致,这样加速度计的求解模型可以简化如下。令XOY共面,并且X轴与理想坐标系的X轴一致。
利用ceres求解,残差函数f=||g||^2-||a||^2构成
3. 仿真及标定程序
(1)利用psins工具箱产生惯导数据
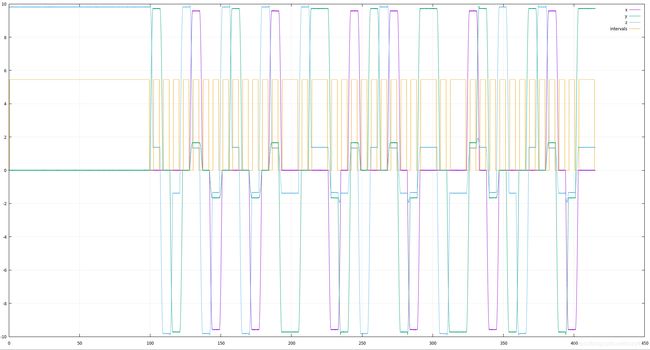
psins工具箱非常强大,使用前需要了解其坐标定义的方式。psins定义的导航坐标系为东北天坐标系,其中yaw角正方向与z轴正方形一致。载体坐标系为右前上坐标系。姿态矩阵定义方式,从导航坐标系旋转到载体坐标系,顺序为:ZXY,对应yaw-pitch-roll.
对惯导数据的要求,标定allan方差和内参所需的数据类型不同。标定allan方差需要静止的2小时以上的数据,标定内参,需要多角度的静止数据。前者比较容易,后者利用test_SINS_trj.m文件产生数据如下。
% Trajectory generation for later simulation use.
% See also test_SINS, test_SINS_GPS_153, test_DR.
% Copyright(c) 2009-2014, by Gongmin Yan, All rights reserved.
% Northwestern Polytechnical University, Xi An, P.R.China
% 10/06/2011, 10/02/2014
% profile on
clear all
glvs
ts = 0.01; % sampling interval
avp0 = avpset([0;0;30], 0, glv.pos0); % init avp
% trajectory segment setting
xxx = [];
seg = trjsegment(xxx, 'init', 0);
seg = trjsegment(seg, 'uniform', 100);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'headup', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
seg = trjsegment(seg, 'rollleft', 2, 45, xxx, 4);
seg = trjsegment(seg, 'uniform', 5);
% generate, save & plot
trj = trjsimu(avp0, seg.wat, ts, 1);
trjfile('trj10ms.mat', trj);
insplot(trj.avp);
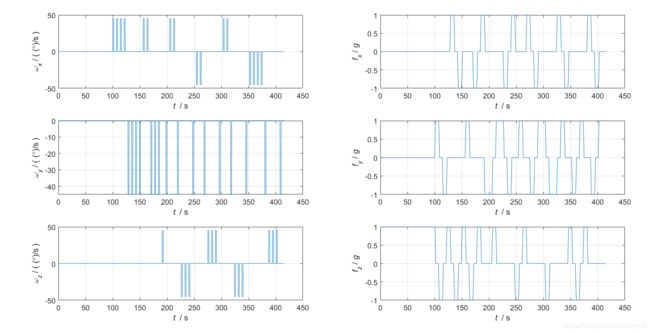
imuplot(trj.imu);
% pos2gpx('trj_SINS_gps', trj.avp(1:round(1/trj.ts):end,7:9)); % to Google Earth
% profile viewer
(2)添加噪声数据
以上产生的惯导数据为没有误差的数据,认为增加噪声来验证allan方差和内参求解的正确性。一下代码基于psins工具箱的环境构建。键入eb、db、web、wdb的噪声,尺度误差DKII,安装误差DKIJ。陀螺仪数据为角增量、加速度计数据为速度增量。
clear all
profile on
glvs
trj = trjfile('trj10ms.mat');
[nn, ts, nts] = nnts(4, trj.ts);
%% set imu error
% Inputs: including information as follows
% eb - gyro constant bias (deg/h)
% db - acc constant bias (ug)
% web - angular random walk (deg/sqrt(h))
% wdb - velocity random walk (ug/sqrt(Hz))
% sqrtR0G,TauG - gyro correlated bias, sqrtR0G in deg/h and TauG in s
% sqrtR0A,TauA - acc correlated bias, sqrtR0A in ug and TauA in s
% dKGii - gyro scale factor error (ppm)
% dKAii - acc scale factor error (ppm)
% dKGij - gyro installation error (arcsec)
% dKAij - acc installation error (arcsec)
% KA2 - acc quadratic coefficient (ug/g^2)
% where,
% |dKGii(1) dKGij(4) dKGij(5)| |dKAii(1) 0 0 |
% dKg = |dKGij(1) dKGii(2) dKGij(6)| , dKa = |dKAij(1) dKAii(2) 0 |
% |dKGij(2) dKGij(3) dKGii(3)| |dKAij(2) dKAij(3) dKAii(3)|
% rxyz - acc inner-lever-arm, =[rx;ry;rz] (cm)
% dtGA - time-asynchrony between gyro & acc, dtGA=Tacc_later-Tgyro_early>0 (ms)
% Output: imuerr - SIMU error structure array
%
% Example:
% For inertial grade SIMU, typical errors are:
% eb=0.01dph, db=50ug, web=0.001dpsh, wdb=10ugpsHz
% scale factor error=10ppm, askew installation error=10arcsec
% sqrtR0G=0.001dph, taug=1000s, sqrtR0A=10ug, taug=1000s
% then call this funcion by
% imuerr = imuerrset(0.01,100,0.001,10, 0.001,1000,10,1000, 10,10,10,10, 10);
eb=3.5; db=100; web=0.5; wdb=10;
dKGii=10;
dKAii=10;
dKGij=10;
dKAij=10;
o31 = zeros(3,1); o33 = zeros(3);
imuerr = struct('eb',o31, 'db',o31, 'web',o31, 'wdb',o31,...
'sqg',o31, 'taug',inf(3,6), 'sqa',o31, 'taua',inf(3,1), 'dKg',o33, 'dKa',o33, 'dKga',zeros(15,1),'KA2',o31);
%% constant bias & random walk
imuerr.eb(1:3) = eb*glv.dph; imuerr.web(1:3) = web*glv.dpsh;
imuerr.db(1:3) = db*glv.ug; imuerr.wdb(1:3) = wdb*glv.ugpsHz;
%% scale factor error
imuerr.dKg = setdiag(imuerr.dKg, dKGii*glv.ppm);
imuerr.dKa = setdiag(imuerr.dKa, dKAii*glv.ppm);
%% installation angle error
dKGij = ones(6,1).*dKGij*glv.sec;
imuerr.dKg(2,1) = dKGij(1); imuerr.dKg(3,1) = dKGij(2); imuerr.dKg(3,2) = dKGij(3);
imuerr.dKg(1,2) = dKGij(4); imuerr.dKg(1,3) = dKGij(5); imuerr.dKg(2,3) = dKGij(6);
dKAij = ones(3,1).*dKAij*glv.sec;
imuerr.dKa(2,1) = dKAij(1); imuerr.dKa(3,1) = dKAij(2); imuerr.dKa(3,2) = dKAij(3);
imuerr.dKga = [imuerr.dKg(:,1); imuerr.dKg(:,2); imuerr.dKg(:,3);
imuerr.dKa(:,1); imuerr.dKa(2:3,2); imuerr.dKa(3,3)];
imu=trj.imu;
[m, n] = size(imu); sts = sqrt(ts);
drift = [ ts*imuerr.eb(1) + sts*imuerr.web(1)*randn(m,1), ...
ts*imuerr.eb(2) + sts*imuerr.web(2)*randn(m,1), ...
ts*imuerr.eb(3) + sts*imuerr.web(3)*randn(m,1), ...
ts*imuerr.db(1) + sts*imuerr.wdb(1)*randn(m,1), ...
ts*imuerr.db(2) + sts*imuerr.wdb(2)*randn(m,1), ...
ts*imuerr.db(3) + sts*imuerr.wdb(3)*randn(m,1) ];
Kg = eye(3)+imuerr.dKg; Ka =eye(3)+ imuerr.dKa;
imu(:,1:6) = [imu(:,1:3)*Kg', imu(:,4:6)*Ka'];
imu(:,1:6) = imu(:,1:6) + drift;
dlmwrite('imudat.txt',imu,'delimiter',',','newline','pc','precision','%.10f');
(3)标定allan方差
imu2= [[imu(:,1:3)/ts, imu(:,4:6)/ts],imu(:,7)];
%由psin仿真出来的数据,为角增量rad、速度增量m/s,所以要除时间
%输入avar里的量为角速度rad/s,加速度m/s^2
%avar为psins里的函数
[adev, tau, Err]=avar(imu2(1:end,1:3),ts);
%calallan参考知乎博客给出,求解出N\K\B等参数
[N,K,B]=calallan(tau,adev);
fprintf('GYR: 零偏不稳定性 %frad/s 或 %fdeg/h \n', B, rad2deg(B)*3600);
fprintf('GYR: 噪声密度(角度随机游走, ARW, Noise density) %f(rad/s)/sqrt(Hz) 或 %f deg/sqrt(h)\n', N, rad2deg(N)*3600^(0.5));
fprintf('GYR: 角速率随机游走, bias variations ("random walks") %f(rad/s)sqrt(Hz) 或 %f deg/h/sqrt(h)\n', K, rad2deg(K) * (3600^(1.5)));
[adev, tau, Err]=avar(imu2(1:end,4:6),ts);
[N,K,B]=calallan(tau,adev);
fprintf('ACC: 零偏不稳定性 %fm/s^(2) 或 %fmg 或 %fug\n', B, B / 9.80665 *1000, B / 9.80665 *1000*1000);
fprintf('ACC: 噪声密度(速率随机游走,VRW, Noise Density, Rate Noise Density) %f(m/s^(2))/sqrt(Hz) 或 %f m/s/sqrt(hr) 或 %f ug/sqrt(Hz)\n', N, N * 3600^(0.5),N / 9.80665 *1000*1000);
fprintf('ACC: 加速度随机游走,bias variations ("random walks") %f(m/s^(2)sqrt(Hz))\n', K);
calallan函数如下
function [ N,K,B ] = calallan( tau,adev )
slope = -0.5;
logtau = log10(tau);
logadev = log10(adev);
dlogadev = diff(logadev) ./ diff(logtau);
[~, i] = min(abs(dlogadev - slope)); %找到slope=-0.5 最接近的点;
% Find the y-intercept of the line.
b = logadev(i) - slope*logtau(i);
% Determine the angle random walk coefficient from the line.
logN = slope*log(1) + b;
disp('random walks')
N = 10^logN ;%角度随机游走值,单位为:(rad/s/root-Hz)
% Plot the results.
tauN = 1;
lineN = N ./ sqrt(tau);
slope = 0.5;
logtau = log10(tau);
logadev = log10(adev);
dlogadev = diff(logadev) ./ diff(logtau);
[~, i] = min(abs(dlogadev - slope));
% Find the y-intercept of the line.
b = logadev(i) - slope*logtau(i);
% Determine the rate random walk coefficient from the line.
logK = slope*log10(3) + b;
disp('rate random walks')
K = 10^logK; %速率随机游走 angle rate random walks (rad/s^2/root-Hz)
% Plot the results.
tauK = 3;
lineK = K .* sqrt(tau/3);
%% Bias Instability
% The above equation is a line with a slope of 0 when plotted on a log-log plot of σ(τ)versusτ.
% The value of B can be read directly off of this line with a scaling of sqrt(2*log(2)/pi) .
slope = 0;
logtau = log10(tau);
logadev = log10(adev);
dlogadev = diff(logadev) ./ diff(logtau);
[~, i] = min(abs(dlogadev - slope));
% Find the y-intercept of the line.
b = logadev(i) - slope*logtau(i);
% Determine the bias instability coefficient from the line.
scfB = sqrt(2*log(2)/pi);
logB = b - log10(scfB);
disp('Bias Instability')
B = 10^logB; %零偏不稳定性 gyros dynamic biases or bias instabilities (radians/s)
% Plot the results.
tauB = tau(i);
lineB = B * scfB * ones(size(tau));
tauParams = [tauN, tauK, tauB];
params = [N, K, scfB*B];
figure
loglog(tau, adev, tau, [lineN, lineK, lineB], '--', tauParams, params, 'o');
title('Allan Deviation with Noise Parameters')
xlabel('\tau')
ylabel('\sigma(\tau)')
legend('\sigma', '\sigma_N', '\sigma_K', '\sigma_B')
text(tauParams, params, {'N', 'K', '0.664B'})
grid on
axis equal
end
结果:
gyro:
acc:
GYR: 零偏不稳定性 0.000011rad/s 或 2.229145deg/h
GYR: 噪声密度(角度随机游走, ARW, Noise density) 0.000146(rad/s)/sqrt(Hz) 或 0.500296 deg/sqrt(h)
GYR: 角速率随机游走, bias variations ("random walks") 0.000001(rad/s)sqrt(Hz) 或 8.501155 deg/h/sqrt(h)
ACC: 零偏不稳定性 0.000004m/s^(2) 或 0.000437mg 或 0.437179ug
ACC: 噪声密度(速率随机游走,VRW, Noise Density, Rate Noise Density) 0.000098(m/s^(2))/sqrt(Hz) 或 0.005891 m/s/sqrt(hr) 或 10.011659 ug/sqrt(Hz)
ACC: 加速度随机游走,bias variations ("random walks") 0.000000(m/s^(2)sqrt(Hz))
由于psins只提供了常值误差、角度随机游走、速度随机游走的设定,所以对比角度随机游走和速度随机游走的结果,和仿真设定参数误差不大。为了验证零篇不稳定性的allan方差结果,增加以下gnss-ins-sim的仿真数据测试。
(4)gnss-ins-sim仿真
设置imu误差的方法,参考官网文档
imu_err = {
# gyro bias, deg/hr
'gyro_b': np.array([0.0, 0.0, 0.0]),
# gyro angle random walk, deg/rt-hr
'gyro_arw': np.array([0.25, 0.25, 0.25]),
# gyro bias instability, deg/hr
'gyro_b_stability': np.array([3.5, 3.5, 3.5]),
# gyro bias instability correlation, sec.
# set this to 'inf' to use a random walk model
# set this to a positive real number to use a first-order Gauss-Markkov model
'gyro_b_corr': np.array([100.0, 100.0, 100.0]),
# accelerometer bias, m/s^2
'accel_b': np.array([0.0e-3, 0.0e-3, 0.0e-3]),
# accelerometer velocity random walk, m/s/rt-hr
'accel_vrw': np.array([0.03119, 0.03009, 0.04779]),
# accelerometer bias instability, m/s^2
'accel_b_stability': np.array([4.29e-5, 5.72e-5, 8.02e-5]),
# accelerometer bias instability correlation, sec. Similar to gyro_b_corr
'accel_b_corr': np.array([200.0, 200.0, 200.0]),
# magnetometer noise std, uT
'mag_std': np.array([0.2, 0.2, 0.2])
}以下为设置的仿真误差:
# -*- coding: utf-8 -*-
# Filename: demo_allan.py
"""
Test Sim with Allan analysis.
Created on 2018-01-23
@author: dongxiaoguang
"""
import os
import math
import numpy as np
from gnss_ins_sim.sim import imu_model
from gnss_ins_sim.sim import ins_sim
# globals
D2R = math.pi/180
motion_def_path = os.path.abspath('.//demo_motion_def_files//')
fs = 100.0 # IMU sample frequency
def test_allan():
'''
An Allan analysis demo for Sim.
'''
#### Customized IMU model parameters, typical for IMU381
imu_err = {'gyro_b': np.array([0.0, 0.0, 0.0]),
'gyro_arw': np.array([0.25, 0.25, 0.25]) * 1.0,
'gyro_b_stability': np.array([3.5, 3.5, 3.5]) * 1.0,
'gyro_b_corr': np.array([100.0, 100.0, 100.0]),
'accel_b': np.array([0.0e-3, 0.0e-3, 0.0e-3]),
'accel_vrw': np.array([0.03119, 0.03009, 0.04779]) * 1.0,
'accel_b_stability': np.array([4.29e-5, 5.72e-5, 8.02e-5]) * 1.0,
'accel_b_corr': np.array([200.0, 200.0, 200.0]),
'mag_std': np.array([0.2, 0.2, 0.2]) * 1.0
}
# do not generate GPS and magnetometer data
imu = imu_model.IMU(accuracy=imu_err, axis=6, gps=False)
#### Allan analysis algorithm
from demo_algorithms import allan_analysis
algo = allan_analysis.Allan()
#### start simulation
sim = ins_sim.Sim([fs, 0.0, 0.0],
motion_def_path+"//motion_def-Allan.csv",
ref_frame=1,
imu=imu,
mode=None,
env=None,
algorithm=algo)
sim.run()
# generate simulation results, summary, and save data to files
sim.results('data/') # save data files
# plot data
sim.plot(['ad_accel', 'ad_gyro'])
if __name__ == '__main__':
test_allan()
结果
gyro:
acc:
GYR: 零偏不稳定性 0.000015rad/s 或 3.001724deg/h
GYR: 噪声密度(角度随机游走, ARW, Noise density) 0.000073(rad/s)/sqrt(Hz) 或 0.249560 deg/sqrt(h)
GYR: 角速率随机游走, bias variations ("random walks") 0.000001(rad/s)sqrt(Hz) 或 13.545860 deg/h/sqrt(h)
ACC: 零偏不稳定性 0.000074m/s^(2) 或 0.007563mg 或 7.562726ug
ACC: 噪声密度(速率随机游走,VRW, Noise Density, Rate Noise Density) 0.000521(m/s^(2))/sqrt(Hz) 或 0.031242 m/s/sqrt(hr) 或 53.096725 ug/sqrt(Hz)
ACC: 加速度随机游走,bias variations ("random walks") 0.000006(m/s^(2)sqrt(Hz))
利用gnss-ins-sim仿真出来的allan方差结果比较接近仿真设置。
(5)利用imu_tk仿真
标定数据要求:利用psins产生imu内参标定的数据。根据imutk这个库的要求,先静止50s,为了标定常值误差,然后转动imu,每个位置做暂时的停留,重复几十次,就可以得到imu的仿真数据。
将仿真数据输入imutk,查看imu_tk的代码注释及论文,可以看到它对误差矩阵的定义方式如下。为了和仿真的下三角矩阵统一,修改来acc的内参矩阵为下三角矩阵:
CalibratedTriad_<_T2> calib_triad(
//
// implement lower triad model here
//
// mis_xz, mis_xy, mis_yx:
_T2(0), _T2(0), _T2(0),
// mis_yz, mis_zy, mis_zx:
params[0], params[1], params[2],
// s_x, s_y, s_z:
params[3], params[4], params[5],
// b_x, b_y, b_z:
params[6], params[7], params[8]
);
//bool MultiPosCalibration_<_T>::calibrateAcc的函数中:
// implement lower triad model here
//
// acc_calib_params[0] = init_acc_calib_.misYZ();
// acc_calib_params[1] = init_acc_calib_.misZY();
// acc_calib_params[2] = init_acc_calib_.misZX();
acc_calib_params[0] = init_acc_calib_.misXZ();
acc_calib_params[1] = init_acc_calib_.misXY();
acc_calib_params[2] = init_acc_calib_.misYX();
acc_calib_params[3] = init_acc_calib_.scaleX();
acc_calib_params[4] = init_acc_calib_.scaleY();
acc_calib_params[5] = init_acc_calib_.scaleZ();
acc_calib_params[6] = init_acc_calib_.biasX();
acc_calib_params[7] = init_acc_calib_.biasY();
acc_calib_params[8] = init_acc_calib_.biasZ();
acc_calib_ = CalibratedTriad_<_T>(
//
// implement lower triad model here
//
0,0,0,
min_cost_calib_params[0],
min_cost_calib_params[1],
min_cost_calib_params[2],
min_cost_calib_params[3],
min_cost_calib_params[4],
min_cost_calib_params[5],
min_cost_calib_params[6],
min_cost_calib_params[7],
min_cost_calib_params[8]
);求解出mis_mat以后,我们可以与我们原始生成的内参矩阵进行对比。
/* Apply undistortion transform to accel measurements
mis_mat_ << _T(1) , -mis_yz , mis_zy ,
mis_xz , _T(1) , -mis_zx ,
-mis_xy , mis_yx , _T(1) ;
scale_mat_ << s_x , _T(0) , _T(0) ,
_T(0) , s_y , _T(0) ,
_T(0) , _T(0) , s_z ;
bias_vec_ << b_x , b_y , b_z ;
define:
ms_mat_ = mis_mat_*scale_mat_
then the undistortion transform:
X' = T*K*(X - B)
can be implemented as:
unbias_data = ms_mat_*(raw_data - bias_vec_)
* assume body frame same as accelerometer frame,
* so bottom left params in the misalignment matris are set to zero */
结果:
Accelerometers calibration: Better calibration obtained using threshold multiplier 10 with residual 0.00204231
Misalignment Matrix
1 -0 0
-0.00277105 1 -0
-0.0120573 -0.0177234 1
Scale Matrix
1.00382 0 0
0 1.00375 0
0 0 1.00391
Bias Vector
0.00098461
0.000970269
0.000980251Accelerometers calibration: inverse scale factors:
0.996192
0.996265
0.996107Gyroscopes calibration: residual 0.00333395
Misalignment Matrix
1 0.00260196 0.0121563
-3.32153e-05 1 0.0175279
-3.28692e-05 -5.44803e-05 1
Scale Matrix
0.999922 0 0
0 1.00051 0
0 0 0.99917
Bias Vector
4.40463e-05
0.000105002
2.34411e-05Gyroscopes calibration: inverse scale factors:
1.00008
0.99949
1.00083
对比真值有差距,可能因为本来偏置就很小,按照光纤陀螺的精度来设置,利用imuTK这种标定mems级别的算法,标定精度没法达到利用转台级别的精度,因为算法本身利用优化方法来进行求解,可以调节迭代优化的推出条件来优化结果。
real acc mis mat:
[[1.00010000e+00 0.00000000e+00 0.00000000e+00]
[4.84567901e-05 1.00010000e+00 0.00000000e+00]
[4.84567901e-05 4.84567901e-05 1.00010000e+00]]
acc mis mat :
[[0.99619454 0. 0. ]
[0.00275019 0.99626401 0. ]
[0.01201319 0.01758841 0.99610523]]
real gyro mis mat:
[[1.00010000e+00 4.84567901e-05 4.84567901e-05]
[4.84567901e-05 1.00010000e+00 4.84567901e-05]
[4.84567901e-05 4.84567901e-05 1.00010000e+00]]
gyro mis mat :
[[ 1.00007752e+00 -2.60149534e-03 -1.21217046e-02]
[ 3.26245539e-05 9.99489220e-01 -1.75338968e-02]
[ 3.29008331e-05 5.44121256e-05 1.00082933e+00]]
但这里先将偏置设置更大一些来验证算法。更改imu的误差仿真数据,常值bias:20deg/h 1000ug,按照MEMS的精度来进行设置。内参KG,KA设置了一个很大的值,因为看到imutk收敛时的residual还是挺大,所以设置一个更大的值去验证算法。
eb=20; db=1000; web=1; wdb=100;
% midmis
Kg=[1.2,0.2,0.2;
0.2,1.2,0.2;
0.2,0.2,1.2];
Ka=[1.2,0,0;
0.2,1.2,0;
0.2,0.2,1.2];
结果:
Misalignment Matrix
1 -0 0
0.00411682 1 -0
-0.0263355 -0.0266324 1
Scale Matrix
0.816568 0 0
0 0.828336 0
0 0 0.836581
Bias Vector
0.00970086
0.0100987
0.0101318Accelerometers calibration: inverse scale factors:
1.22464
1.20724
1.19534Misalignment Matrix
1 -0.295704 -0.230885
-0.114036 1 -0.277286
-0.141129 -0.146999 1
Scale Matrix
0.910992 0 0
0 0.873403 0
0 0 0.900472
Bias Vector
0.000159544
0.000128604
0.000130498Gyroscopes calibration: inverse scale factors:
1.0977
1.14495
1.11053
real acc mis mat:
[[1.2 0. 0. ]
[0.2 1.2 0. ]
[0.2 0.2 1.2]]
acc mis mat :
[[ 1.22463775 0. 0. ]
[-0.00608643 1.20723957 0. ]
[ 0.03835773 0.03843225 1.19534152]]
real gyro mis mat:
[[1.2 0.2 0.2]
[0.2 1.2 0.2]
[0.2 0.2 1.2]]
gyro mis mat :
[[1.23243613 0.49615979 0.46878657]
[0.23438371 1.30188894 0.46099297]
[0.23141936 0.29029099 1.25925613]]
内参和bias的结果和仿真真值大致在一个量级上吧,精度一般,可以尝试调节ceres的条件优化精度。
参考链接:
- https://zhuanlan.zhihu.com/p/294887884 《MEMS IMU的噪声和误差源2(allan方差)》
- http://www.psins.org.cn/ 《psins工具箱、惯导教材、数据》
- imu_utils下载地址为: https://github.com/gaowenliang/imu_utils
- code_utils下载地址为: https://github.com/gaowenliang/code_utils
- gnss-ins-sim下载: https://github.com/Aceinna/gnss-ins-sim