图像分析：投影曲线的波峰查找

1. 前言

在图像分析里，投影曲线是我们经常要用到的一个图像特征，通过投影曲线我们可以看到在某一个方向上，图像灰度变化的规律，这在图像分割，文字提取方面应用比较广。一个投影曲线，它的关键信息就在于波峰与波谷，所以我们面临的第一个问题就是找到波峰与波谷。

第一次涉及到求波峰与波谷时，很多人都不以为意，觉得波谷波峰还不容易，无非是一些曲线变化为零的点，从离散的角度来说，也就是:

波峰：F(x)>F(x−1)且F(x)>F(x+1)F(x)>F(x−1)且F(x)>F(x+1)

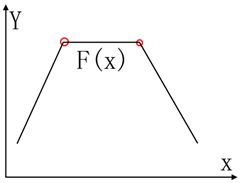
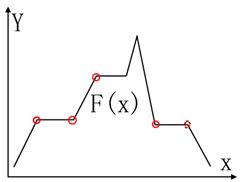
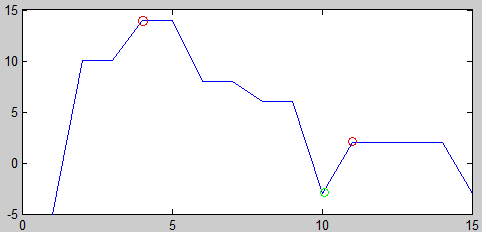
波谷：F(x)

这么简单吗？显示不是，你首先就会遇到这样的曲线图，然后图上的波峰点并不满足上面的条件。

看到这种情况，你也许会考虑在上面的等式中把>>和<<改为≥≥和≤≤。

波峰：F(x)≥F(x−1)&&F(x)>F(x+1)F(x)≥F(x−1)&&F(x)>F(x+1)  或者 F(x)>F(x−1)&&F(x)≥F(x+1)F(x)>F(x−1)&&F(x)≥F(x+1)

波谷：F(x)≤F(x−1)&&F(x)

这次是否就这样简单，答案显示不是，下面的这个图就会让你对一些非峰值点作出错误的判断。

上面这幅图真正的峰值只有一个，其他平台上的点，你如果按上面修改的公式，就会被错误的当成波峰点。

下面让我们看一下，到底如何能求得准确的曲线波峰与波谷。

2. 波峰波谷算法

投影曲线实际上是一个一维的向量：

V=[v1,v2,…,vn]V=[v1,v2,…,vn]

其中vi,i∈[1,2,…,N]vi,i∈[1,2,…,N]，代表图像在第ii行或列上的灰度累积。当然不仅仅是投影曲线，TT也可以是某一事件中变量的观测值，我们需要研究这个变量的变化规律。

下面给出波峰与波谷的算法：

1，假投影曲线可以表示为V=[v1,v2,…,vn]V=[v1,v2,…,vn]。

2，计算V的一阶差分向量DiffVDiffV:

Diffv(i)=V(i+1)−V(i),其中i∈1,2,…,N−1Diffv(i)=V(i+1)−V(i),其中i∈1,2,…,N−1

3,对差分向量进行取符号函数运算，Trend=sign(Diffv)Trend=sign(Diffv),即遍历DiffvDiffv，若Diffv(i)Diffv(i)大于0，则取1；如果小于0，则取-1，否则则值为0。

sign(x)=⎧⎩⎨10−1  if  x>0  if  x=0  if  x<0sign(x)={1  if  x>00  if  x=0−1  if  x<0

4，从尾部遍历TrendTrend向量,进行如下操作：

if Trend(i)=0且Trend(i+1)≥0，则Trend(i)=1if Trend(i)=0且Trend(i+1)<0，则Trend(i)=−1if Trend(i)=0且Trend(i+1)≥0，则Trend(i)=1if Trend(i)=0且Trend(i+1)<0，则Trend(i)=−1

5，对TrendTrend向量进行一阶差分运算，如同步骤2，得到R=diff(Trend)R=diff(Trend)。

6，遍历得到的差分向量RR，如果R(i)=−2R(i)=−2，则i+1i+1为投影向量VV的一个峰值位，对应的峰值为V(i+1)V(i+1)；如果R(i)=2R(i)=2，则i+1i+1为投影向量VV的一个波谷位，对应的波谷为V(i+1)V(i+1)。

下面我们来结合一个实际的向量值，给中中间结合的计算。

1，V=[−5,10,10,14,14,8,8,6,6,−3,2,2,2,2,−3]V=[−5,10,10,14,14,8,8,6,6,−3,2,2,2,2,−3]。

它的曲线图像如下把示，图中红色圈标出了曲线的峰值，而绿字圈标出了图像的波谷位置。

2，计算VV的一阶差分，我们得到Diff(V)=[15,0,4,0,,−6,0,−2,0,−9,5,0,0,0,−5]Diff(V)=[15,0,4,0,,−6,0,−2,0,−9,5,0,0,0,−5]。

3，对DiffvDiffv进行取符号运算，得到向量Trend=[1,0,1,0,−1,0,−1,0,−1,1,0,0,0,−1]Trend=[1,0,1,0,−1,0,−1,0,−1,1,0,0,0,−1]。

4，对TrendTrend作一次遍历，如步骤4。Trend=[1,1,1,−1,−1,−1,−1,−1,−1,1,−1,−1,−1,−1]Trend=[1,1,1,−1,−1,−1,−1,−1,−1,1,−1,−1,−1,−1]。

5，对TrendTrend做一阶差分，得到向量R=Diff(Trend)=[0,0,−2,,0,0,0,0,0,2,−2,0,0,0]R=Diff(Trend)=[0,0,−2,,0,0,0,0,0,2,−2,0,0,0]。

6，遍历向量RR,我们就得到了两个峰值点和一个波谷点。

3. 算法原理

其实上述算法的核心思路非常简单，曲线的峰值点，满足一阶导数为0，并且满足二阶导数为负；而波谷点，则满足一阶导数为0，二阶导数为正。

在上面的算法里面，我们首先计算了一阶的导数DiffvDiffv，然后我们将其符号化，是因为我们并不关心一阶导数的大小。

然后我们去看那些一阶层数为0的地方，我们发现，那些平台上的点，有些并不是波峰与波谷，然后很多处在上坡与下坡的路上，所以我们将它们的一阶导数设为与它们所在的坡面梯度方向相同。

最后我们再来计算二阶导数时，就会发现只要为2或者-2,所以曲线斜在这个点发生了变化，由正变负或由负变正。找到这些点，也就找到了原曲线中的波峰或波谷点。

4. 实现

下面给出这个算法的C++实现，findPeaks是查找波峰函数，而查找波谷函数则类似，这里没有写在一个函数内。函数接受一个Vecotr的向量，输出为一个vector的位置向量。

void findPeak(const vector& v, vector& peakPositions)
{
    vector diff_v(v.size() - 1, 0);
    // 计算V的一阶差分和符号函数trend
    for (vector::size_type i = 0; i != diff_v.size(); i++)
    {
        if (v[i + 1] - v[i]>0)
            diff_v[i] = 1;
        else if (v[i + 1] - v[i] < 0)
            diff_v[i] = -1;
        else
            diff_v[i] = 0;
    }
    // 对Trend作了一个遍历
    for (int i = diff_v.size() - 1; i >= 0; i--)
    {
        if (diff_v[i] == 0 && i == diff_v.size() - 1)
        {
            diff_v[i] = 1;
        }
        else if (diff_v[i] == 0)
        {
            if (diff_v[i + 1] >= 0)
                diff_v[i] = 1;
            else
                diff_v[i] = -1;
        }
    }

    for (vector::size_type i = 0; i != diff_v.size() - 1; i++)
    {
        if (diff_v[i + 1] - diff_v[i] == -2)
            peakPositions.push_back(i + 1);
    }
}

​​